标签:efi cst memset tmp can lazy class turn int
某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。某天,雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。
输入导弹依次飞来的高度(雷达给出的高度数据是不大于30000的正整数,导弹数不超过1000),计算这套系统最多能拦截多少导弹,如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
输入只有一行,为若干个正整数,一次为导弹的高度。
第一行为最多能拦截的导弹数;
第二行为要拦截所有导弹最少要配备的系统数
389 207 155 300 299 170 158 65
6
2
#include <bits/stdc++.h>
using namespace std;
const int maxn=1010;
int a[maxn],dp1[maxn],dp2[maxn];
int cnt,tot,minnum;
int main(){
while(~scanf("%d",&a[++cnt]));
cnt--;
for(int i=1;i<=cnt;i++){
dp1[i]=dp2[i]=1;
for(int j=1;j<i;j++){
if(a[i]<=a[j])
dp1[i]=max(dp1[i],dp1[j]+1);
if (a[i]>a[j])
dp2[i]=max(dp2[i],dp2[j]+1);
}
tot=max(tot,dp1[i]);
minnum=max(minnum,dp2[i]);
}
cout<<tot<<endl<<minnum;
return 0;
}
在一个地图上有N个地窖(N<=200),每个地窖中埋有一定数量的地雷。同时,给出地窖之间的连接路径,并规定路径都是单向的,也不存在可以从一个地窖出发经过若干地窖后又回到原来地窖的路径。
某人可以从任一处开始挖地雷,然后沿着指出的连接往下挖(仅能选择一条路径),当无连接时挖地雷工作结束。设计一个挖地雷的方案,使他能挖到最多的地雷。
第一行一个整数n表示有n个地窖
第二行有n个整数表示每个地窖的地雷数
以下有若干行,每行有两个数x,y表示x可以到y,保证x小于y。
最后一行有两个0,表示输入结束
第一行输出挖地雷的顺序。
第二行为最多挖出的地雷数
6
5 10 20 5 4 5
1 2
1 4
2 4
3 4
4 5
4 6
5 6
0 0
3-4-5-6
34
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1e3+10;
int w[N],f[N],pre[N];
bool g[N][N];
void print(int t){
if(pre[t]){
print(pre[t]);
printf("-%d",t);
}else printf("%d",t);
}
int main(){
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&w[i]);
f[i]=w[i];
}
int a,b;
while(~scanf("%d%d",&a,&b)&&a&&b){
g[a][b]=1;
}
int ans=0,t=0;
for(int i=1;i<=n;i++){
for(int j=1;j<i;j++){
if(g[j][i]){
if(f[j]+w[i]>f[i]){
pre[i]=j;
f[i]=f[j]+w[i];
}
}
if(ans<f[i]){
ans=f[i];
t=i;
}
}
}
print(t);
printf("\n%d",ans);
}
鹰最骄傲的就是翱翔,但是鹰们互相都很嫉妒别的鹰比自己飞的快,更嫉妒其他的鹰比自己飞行的有技巧。于是,他们决定举办一场比赛,比赛的地方将在一个迷宫之中。
这些鹰的起始点被设在一个N*M矩阵的左下角map[1,1]的左下角。终点被设定在矩阵的右上角map[N,M]的右上角,有些map[i,j]是可以从中间穿越的。每一个方格的边长都是100米。如图所示:
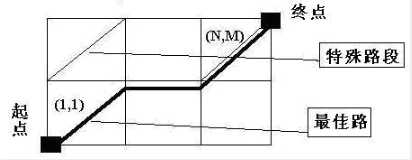
没有障碍,也没有死路。这样设计主要是为了高速飞行的鹰们不要发现死路来不及调整而发生意外。
潘帕斯雄鹰冒着减RP的危险从比赛承办方戒备森严的基地中偷 来了施工的地图。但是问题也随之而来,他必须在比赛开始之前把地图的每一条路都搞清楚,从中找到一条到达终点最近的路。(哈哈,笨鸟不先飞也要拿冠军)但 是此鹰是前无古鹰,后无来鹰的吃菜长大的鹰--菜鸟。他自己没有办法得出最短的路径,于是紧急之下找到了学OI的你,希望找到你的帮助。
首行为n,m(0<n,m<=1000000),第2行为k(0<k<=1000)表示有多少个特殊的边。以下k行为两个数,i,j表示map[i,j]是可以直接穿越的。
仅一行,(1,1)-->(n,m)的最短路径的长度,四舍五入保留到整数即可
3 2
3
1 1
3 2
1 2
383
#include <bits/stdc++.h>
using namespace std;
#define cle(a) memset(a,0,sizeof(a))
//#define int long long
const int maxn=1500;
const int Inf=0x3f3f3f3f;
int dp[maxn];
int sum;
struct node{int x,y;}a[maxn];
bool cmp(node a,node b){
return a.x<b.x;
}
int main(){
int n,m,k;cin>>n>>m>>k;
for(int i=1;i<=k;i++)
cin>>a[i].x>>a[i].y;
sort(a+1,a+k+1,cmp);
for(int i=1;i<=k;i++)
for(int j=i+1;j<=k;j++)
if(a[j].x>a[i].x && a[j].y>a[i].y && dp[i]+1>dp[j])
dp[j]=dp[i]+1;
for(int i=1;i<=k;i++)
sum=max(dp[i],sum);
sum++;
double len=2-sqrt(2),ans=(m+n-sum*len)*100;
cout<<int (ans+0.5);
return 0;
}
Ural 大学有 N 个职员,编号为 1~N。他们有从属关系,也就是说他们的关系就像一棵以校长为根的树,父结点就是子结点的直接上司。每个职员有一个快乐指数。现在有个周年庆宴会,要求与会职员的快乐指数最大。但是,没有职员愿和直接上司一起与会。
第一行一个整数 N。(1<=N<=6000)
接下来 N 行,第 i+1 行表示 i 号职员的快乐指数
接下来 N-1 行,每行输入一对整数 L,K。表示 K 是 L 的直接上司。
最后一行输入 0,0。
输出最大的快乐指数。
7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5
0 0
5
#include <bits/stdc++.h>
using namespace std;
const int maxn=6500;
const int Inf=0x3f3f3f3f;
int dp[maxn][maxn],jl[maxn];
int map_[maxn][maxn];
int r[maxn],tot[maxn],cnt[maxn];
int tmp,ans;
void tree_dp(int root){
for(int i=0;i<tot[root];i++){
int tmp=map_[root][i];
tree_dp(tmp);
dp[root][0]+=max(dp[tmp][1],dp[tmp][0]);
dp[root][1]+=dp[tmp][0];
}
dp[root][1]+=r[root];
}
int main(){
int n;cin>>n;
for(int i=1;i<=n;i++){
cin>>r[i];
}
int l,k;
for(int i=1;i<=n;i++){
cin>>l>>k;
map_[k][tot[k]++]=l;
cnt[l]++;
}
for(int i=1;i<=n;i++)
if(cnt[i]==0){
tree_dp(i);
cout<<max(dp[i][1],dp[i][0]);
return 0;
}
return 0;
}
标签:efi cst memset tmp can lazy class turn int
原文地址:https://www.cnblogs.com/hellohhy/p/13195515.html