标签:ret return 就是 思路 返回 print names swap def
https://www.luogu.com.cn/problem/P1967
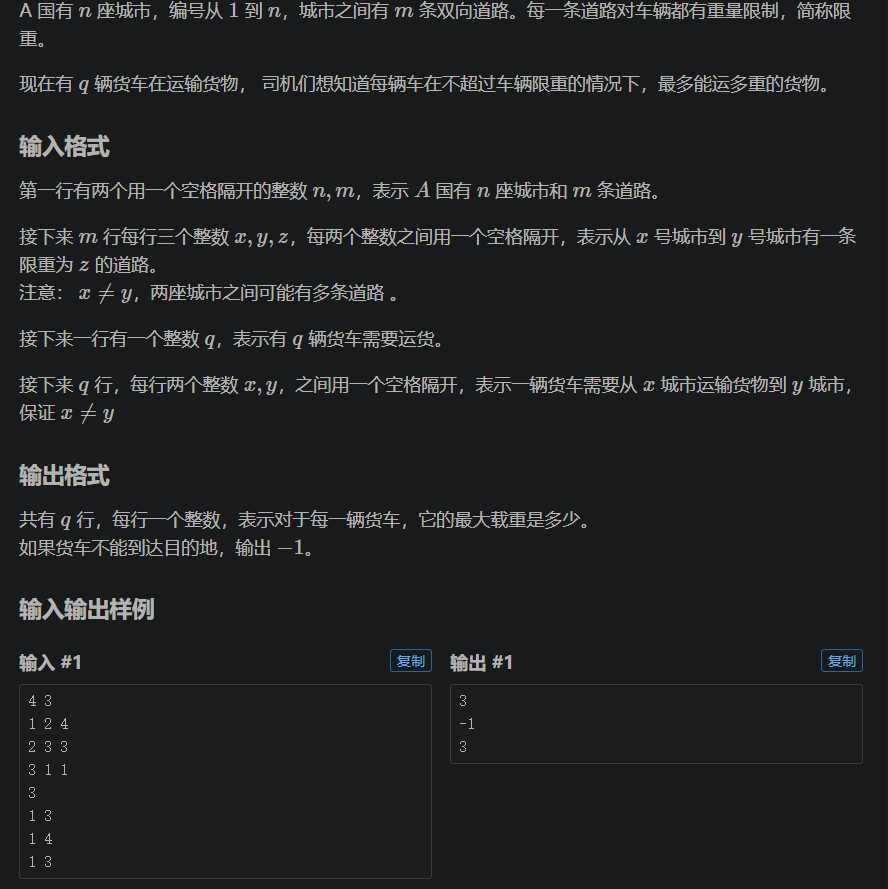
分析题目我们可以知道,图中两点之间的路径是不唯一的,而且我们根据题意可以知道在选择路径的时候要尽量选择限重比较大的值,
对于两点u,v,如果u->v中最小的边的权值最大,那么这条路径u−>v一定在最大生成树上。这里的思路就是我们可以使用最大生成树来求解路径
但是如何求出两个节点之间最小边权的最大值?因为这两点之间的路径是唯一的,我们只需要找出这条路径便可以得到答案。
我们可以通过LCA来做到这一点,我求LCA的方法是先从每一个根节点进行搜索,求出节点深度等信息,然后利用这些信息进行树上倍增
#include<iostream> #include<cstdio> #include<cmath> #include<algorithm> #include<string> #include<cstring> #define maxn 10005 #define inf 0x3f3f3f3f #define maxm 5*maxn using namespace std; struct edge { int to; int dis; int next; }e[maxm*2]; struct node { int from; int to; int dis; }list[maxm]; bool cmp(struct node &a, struct node &b) { return a.dis > b.dis; } int head[maxn], father[maxn],deep[maxn],vis[maxn], father2[maxn][22],w[maxn][22], cnt = 0; int n, m,q; //father是并查集使用的 w数组表示最大载重 void addedge(int u,int v,int w) { cnt++; e[cnt].to = v; e[cnt].dis = w; e[cnt].next = head[u]; head[u] = cnt; } int find(int x) { if (father[x] == x)return x; return father[x] = find(father[x]); } void dfs(int node) { vis[node] = 1; for (int i = head[node]; i; i = e[i].next) { int y = e[i].to; if (vis[y])continue; deep[y] = deep[node] + 1; father2[y][0] = node;//储存父节点 w[y][0] = e[i].dis;//储存到父节点的权值 dfs(y); } } void kruskal() { sort(list+1, list + m+1, cmp); for (int i = 1; i <=m; i++) { int tempx = find(list[i].from); int tempy = find(list[i].to); if (tempx == tempy)continue; father[tempx] = tempy; addedge(list[i].from, list[i].to, list[i].dis); addedge(list[i].to, list[i].from, list[i].dis); } } int lca(int x,int y) { if (find(x) != find(y))return -1; int ans = inf; if (deep[x] > deep[y])swap(x, y); for (int i = 20; i >= 0; i--) //将y节点上提到于x节点相同深度 { if (deep[father2[y][i]] >= deep[x]) { ans = min(ans, w[y][i]); //更新最大载重(最小边权) y = father2[y][i];//修改y位置 } } if (x == y)return ans;//如果位置已经相等,直接返回答案 for (int i = 20; i >= 0; i--) { if (father2[x][i]!=father2[y][i]) { ans = min(w[x][i],min(ans, w[y][i]));//更新最大载重(最小边权) y = father2[y][i];//X Y共同更新 x = father2[x][i]; } } ans = min(ans, min(w[x][0], w[y][0])); //更新此时x,y到公共祖先最大载重,fa[x][0], fa[y][0]即为公共祖先 return ans; } int main() { scanf("%d%d", &n, &m); for (int i = 1; i <=m; i++) { scanf("%d%d%d", &list[i].from, &list[i].to, &list[i].dis); } for (int i = 0; i <= n; i++)father[i] = i; kruskal(); for (int i = 1; i <= n; i++) { if (!vis[i]) { deep[i] = 1; dfs(i); father2[i][0] = i; w[i][0] = inf; } } for (int i = 1; i <= 20; i++) for (int j = 1; j <= n; j++) { father2[j][i] = father2[father2[j][i - 1]][i - 1]; w[j][i] = min(w[j][i - 1], w[father2[j][i - 1]][i - 1]); } scanf("%d", &q); for (int i = 1; i <= q; i++) { int x, y; scanf("%d%d", &x, &y); printf("%d\n", lca(x, y)); //回答询问 } }
标签:ret return 就是 思路 返回 print names swap def
原文地址:https://www.cnblogs.com/Jason66661010/p/13195997.html