标签：sid   span   基础上   fun   upper   table   log   order   alt   

------------恢复内容开始------------

Range Sum Query 2D - Immutable (M)

题目

Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

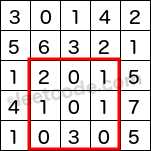
The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.

Example:

Given matrix = [
  [3, 0, 1, 4, 2],
  [5, 6, 3, 2, 1],
  [1, 2, 0, 1, 5],
  [4, 1, 0, 1, 7],
  [1, 0, 3, 0, 5]
]

sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12

Note:

1. You may assume that the matrix does not change.
2. There are many calls to sumRegion function.
3. You may assume that row1 ≤ row2 and col1 ≤ col2.

题意

给定一个整数矩阵，求其中一个子矩阵的数字之和。

思路

一种方法是在 0303. Range Sum Query - Immutable 的基础上，将矩阵中每一行的sum情况缓存，求指定矩阵和时，只要累加该矩阵每一行对应的sum值即可。

更好的策略是将一维缓存的方法进行推广，进行二维缓存：

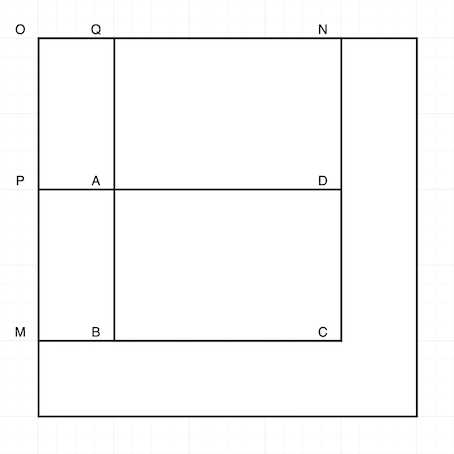
\(S_{ABCD} = S_{OMCN} - S_{OMBQ} - S_{OPDN} + S_{OPAQ} = S_{OC} - S_{OB} - S_{OD} + S_{OA}\)

代码实现

Java

一维缓存

class NumMatrix {
    private int[][] sum;

    public NumMatrix(int[][] matrix) {
        if (matrix.length != 0) {
            sum = new int[matrix.length][matrix[0].length + 1];
            for (int i = 0; i < matrix.length; i++) {
                for (int j = 0; j < matrix[0].length; j++) {
                    sum[i][j + 1] += sum[i][j] + matrix[i][j];
                }
            }
        }
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        int total = 0;
        for (int i = row1; i <= row2; i++) {
            total += sum[i][col2 + 1] - sum[i][col1];
        }
        return total;
    }
}

二维缓存

class NumMatrix {
    private int[][] sum;

    public NumMatrix(int[][] matrix) {
        if (matrix.length > 0) {
            int m = matrix.length, n = matrix[0].length;
            sum = new int[m + 1][n + 1];
            for (int i = 0; i < m; i++) {
                for (int j = 0; j < n; j++) {
                    sum[i + 1][j + 1] = sum[i + 1][j] + sum[i][j + 1] + matrix[i][j] - sum[i][j];
                }
            }
        }
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        return sum[row2 + 1][col2 + 1] - sum[row2 + 1][col1] - sum[row1][col2 + 1] + sum[row1][col1];
    }
}

------------恢复内容结束------------

0304. Range Sum Query 2D - Immutable (M)

标签：sid   span   基础上   fun   upper   table   log   order   alt   

原文地址：https://www.cnblogs.com/mapoos/p/13197184.html