数据结构第七章学习总结

标签：二次   info   排列   分析   情况   所有结点   顺序表   顺序查找   二分查找算法   

一、第七章内容小结

1. 查找的基本概念

2. 线性表的查找

① 顺序查找：从表的一端开始依次将记录的关键字和给定值进行比较，某记录的关键字和定值相等则查找成功；反之，扫描整个表未找到相等记录，则查找失败。顺序查找适用于线性表的顺序存储结构和链式存储结构。

2-1基于顺序表的顺序查找算法：

1 int Search_Seq(SSTable ST, KeyType key)
2 {//若找到则返回元素在表中的位置，反之则返回0
3    for(i=ST.length; i>=1; --i)
4       if(ST.R[i].key==key) return i;     //往后面找
5       return 0;            
6 }

2-2设置监视哨的顺序查找算法：

1 int Search_Seq(SSTable ST, KeyType key)
2 {
3    ST.R[0].key=key;                                        // 哨兵
4    forI(i=ST.length; ST.R[i].ley!=key; --i);         // 从后往前找
5    return i;  
6 }
7 /*
8 通过设置监视哨，免去查找过程中每一步都要检测整个表是否查找完毕。表长较长时，进行一次查找所需的平均时间几乎减少一半。
9 */

# 2-1和2-2时间复杂度一样，均为O(n)

② 折半查找：也称二分查找，要求线性表必须采用顺序存储机构，且元素有序排列。

二分查找算法：

 # 注意：循环执行条件为low<=high, 而不是low<high, 因为low=high时查找区间还有最后一个结点，还要进一步比较。

 # 二分查找时间复杂度为O(log2n)

③ 分块查找：又称索引顺序查找，介于顺序查找和折半查找之间的一种查找方法。需在本表以外另建立一个索引表。索引表按关键字有序，则表或者有序或者分块有序。所谓分块有序，即是第二个子表中的所有关键字均大于第一个子表中的最大关键字，后续以此类推。

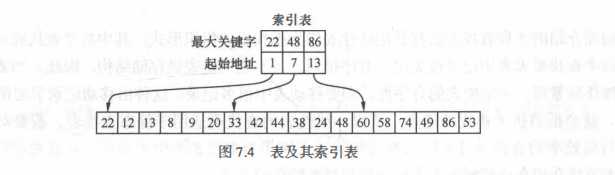
 例：

 ASL = Lb + Lw   (Lb为查找所在块平均查找长度，Lw为在块中查找平均查找长度)

3. 树表的查找

 3-1 二叉排序树：若左子树不空则左子树上所有结点的值均小于根结点的值；

　　　　　　　　若右子树不空则右子树上所有结点的值均大于根结点的值；

　　　　　　　　左、右子树均为二叉排序树。

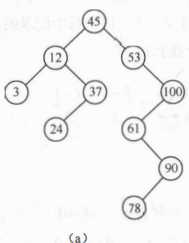
 二叉排序树的递归查找：

 # 树的深度为n， 则平均查找长度为n+1/2

二叉排序树的插入：

 二叉排序树的创建：

3-2 平衡二叉树：左子树和右子树深度之差绝对值不超过1，左右子树也是平衡二叉树。

3-3 B-树：多叉树，一层有多个关键字。可减小高度，避免内外存反复的交换。

3-4 B+树：类似B-树，可实现区间查找。

4. 散列表的查找

4-1 构造方法：

①数字分析法：仅适用于事先知道关键字集合。

②平方取中法：适用于不能事先了解关键字的所有情况，或难于直接从关键字中找到取值较分散的几位。

③折叠法：适用于散列地址的位数较少，而关键字的位数较多。

④除留余数法：最常用的构造散列函数的方法，选p为小于表长的最大质数。

4-2 处理冲突的方法

①开放地址法：

a) 线性探测法：从冲突地址的下一单元顺序寻找空单元，如果最后一个位置也没找到空单元，则回到表头开始继续查找。如果找不到空位，说明散列表已满，需要进行溢出处理。

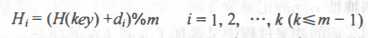
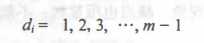
b) 二次探测法：正增量为往后查找，负增量为往前查找

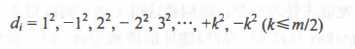
c) 伪随机探测法

②链地址法：类似邻接表，将所有冲突的地址以链式存储的形式放在相应位置的后面。

数据结构第七章学习总结

标签：二次   info   排列   分析   情况   所有结点   顺序表   顺序查找   二分查找算法   

原文地址：https://www.cnblogs.com/cbs-2397812053/p/13196309.html