标签：ati 入门 exp 就是 阈值 图片 维数 lse 保存
，函数图像如下：
# 用python画阶跃函数图 import numpy as np import matplotlib.pylab as plt def step_function(x): """ =============step.1============ if x > 0: return 1 else: return 0 这段代码可以简化为 y = x > 0 =============step.2============ return y 若是这样，参数x只能接受实数（浮点数），即只允许形如 step_function(3.0)的调用，而不允许参数取NumPy数组。 修改为支持NumPy数组的实现的代码为：return y.astype(np.int)， 如step_function(np.array([1.0, 2.0]) y.astype(np.int)使y从布尔型数组转换为int型数组 return y.astype(np.int) =============step.3============ step.1和step.2可以简化为return np.array(x > 0, dtype = np.int) """ return np.array(x > 0, dtype=np.int) # 在-5.0到5.0的范围内，以0.1为单位，生成NumPy数组 # ([-5.0, -4.9, ..., 4.9])，注意：右端点不是5.0而是4.9 x = np.arange(-5.0, 5.0, 0.1) y = step_function(x) plt.plot(x, y) plt.ylim(-0.1, 1.1) # 指定y轴的范围 plt.show()
运行结果：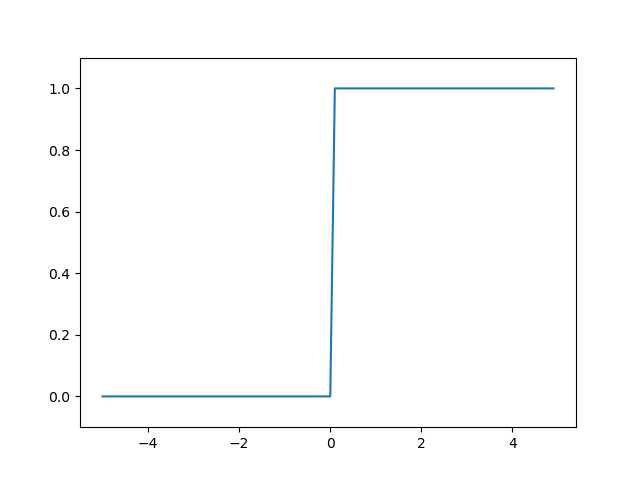
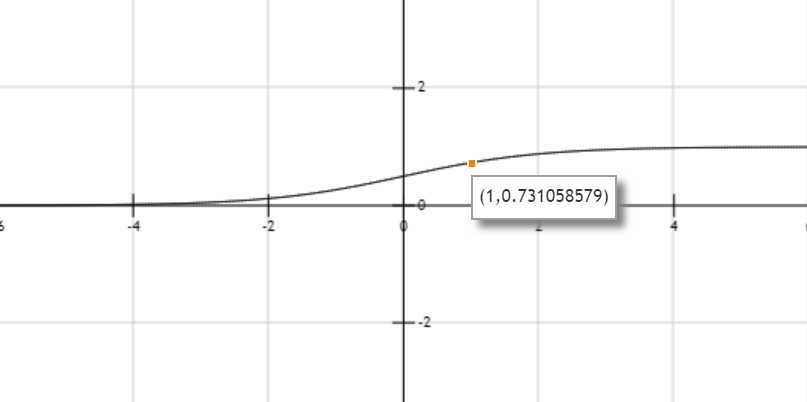
import numpy as np import matplotlib.pylab as plt def sigmoid(x): return 1 / (1 + np.exp(-x)) x = np.arange(-5.0, 5.0, 0.1) y = sigmoid(x) plt.plot(x, y) plt.ylim(-0.1, 1.1) # 指定y轴的范围 plt.show()
运行结果：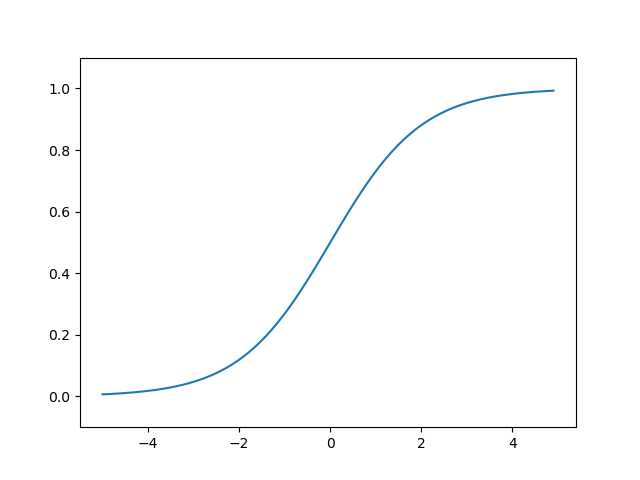
阶跃函数与sigmoid函数均为非线性函数，前者为曲线，后者为折线。
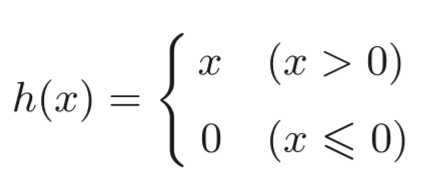，ReLU函数在输入大于0时，直接输出该值，否则输出0import numpy as np import matplotlib.pylab as plt def relu(x): return np.maximum(0, x) # x大于0时输出x, x小于等于0（0大于x）时输出0 x = np.arange(-5.0, 5.0, 0.1) y = relu(x) plt.plot(x, y) plt.ylim(-1.0, 5.1) # 指定y轴的范围 plt.show()
运行结果：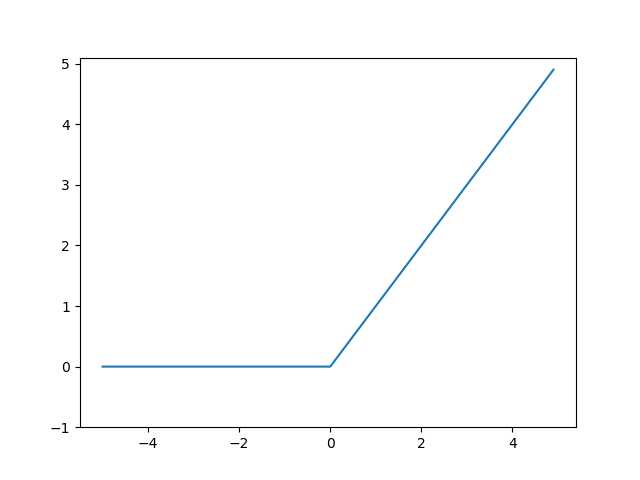
import numpy as np def sigmoid(x): return 1 / (1 + np.exp(-x)) X = np.array([1.0, 0.5]) # 第一层 W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]]) B1 = np.array([0.1, 0.2, 0.3]) A1 = np.dot(X, W1) + B1 Z1 = sigmoid(A1) # 第二层 W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]]) B2 = np.array([0.1, 0.2]) A2 = np.dot(A1, W2) + B2 Z2 = sigmoid(A2) # 输出 # 定义恒等函数identity_function()作为输出层的激活函数 """ 输出层所用的激活函数要根据求解问题的性质来决定。 一般而言，回归问题可以使用恒等函数，二元分类问题可以使用sigmoid函数， 多元分类问题可以使用softmax函数 """ def identity_function(x): return x W3 = np.array([[0.1, 0.3], [0.2, 0.4]]) B3 = np.array([0.1, 0.2]) A3 = np.dot(Z2, W3) + B3 Y = identity_function(A3)
代码整理如下：
import numpy as np def sigmoid(x): return 1 / (1 + np.exp(-x)) def identity_function(x): return x def init_network(): network = {} network[‘W1‘] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]]) network[‘b1‘] = np.array([0.1, 0.2, 0.3]) network[‘W2‘] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]]) network[‘b2‘] = np.array([0.1, 0.2]) network[‘W3‘] = np.array([[0.1, 0.3], [0.2, 0.4]]) network[‘b3‘] = np.array([0.1, 0.2]) return network def forward(network, x): W1, W2, W3 = network[‘W1‘], network[‘W2‘], network[‘W3‘] b1, b2, b3 = network[‘b1‘], network[‘b2‘], network[‘b3‘] a1 = np.dot(x, W1) + b1 z1 = sigmoid(a1) a2 = np.dot(z1, W2) + b2 z2 = sigmoid(a2) a3 = np.dot(z2, W3) + b3 y = identity_function(a3) return y network = init_network() x = np.array([1.0, 0.5]) y = forward(network, x) print(y) # [0.31682708 0.69627909]
init_network()进行权重和偏置初始化，并将它们保存在字典变量network中，forward()函数则封装了将输入信号转换为输出信号的处理过程
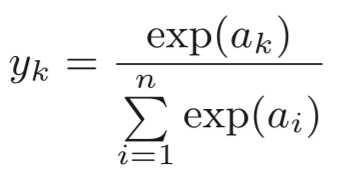
import numpy as np # 完全根据公式来实现的softmax函数具有一定缺陷 def softmax_tmp(a): exp_a = np.exp(a) sum_exp_a = np.sum(exp_a) y = exp_a / sum_exp_a return y """ 上面的softmax_tmp()函数虽然正确描述了softmax函数的公式，但存在溢出问题。 softmax函数中的指数运算会得到非常大的值，如e^1000会返回一个表示无穷大的inf。 在这些超大值之间进行除法运算会使结果出现”不确定“的情况 计算机处理“数”时，数值必须在4字节或8字节的有限数据宽度内，这意味着数存在有效位数， 因此会出现超大值无法表示的问题，即溢出问题 在进行softmax的指数函数的运算时，加上或减去某个常数并不会改变运算结果 """ # 修改后的softmax函数如下： def softmax(a): c = np.max(a) exp_a = np.exp(a - c) # 溢出对策 sum_exp_a = np.sum(exp_a) y = exp_a / sum_exp_a return y
标签：ati 入门 exp 就是 阈值 图片 维数 lse 保存
原文地址：https://www.cnblogs.com/s-zhou/p/13200460.html
