leetcode题解之37. 解数独

时间：2020-06-28 00:13:01 阅读：71 评论：0 收藏：0 [点我收藏+]

标签：算法 tin adc 次数 ber ISE elements 程序提示

编写一个程序，通过已填充的空格来解决数独问题。

一个数独的解法需遵循如下规则：

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

空白格用 ‘.‘ 表示。

一个数独。

答案被标成红色。

Note:

给定的数独序列只包含数字 1-9 和字符 ‘.‘ 。
你可以假设给定的数独只有唯一解。
给定数独永远是 9x9 形式的。

方法 0：蛮力法

首先的想法是通过蛮力法来生成所有可能用1 到 9填充空白格的解，
并且检查合法从而保留解。这意味着共有 $9^{81}$ 个操作需要进行。
其中 $9$ 是可行的数字个数， $81$ 是需要填充的格子数目。
因此我们必须考虑进一步优化。

方法 1：回溯法

使用的概念

了解两个编程概念会对接下来的分析有帮助。

第一个叫做 约束编程。

基本的意思是在放置每个数字时都设置约束。在数独上放置一个数字后立即
排除当前行，列和 子方块 对该数字的使用。这会传播 约束条件 并有利于减少需要考虑组合的个数。

技术图片

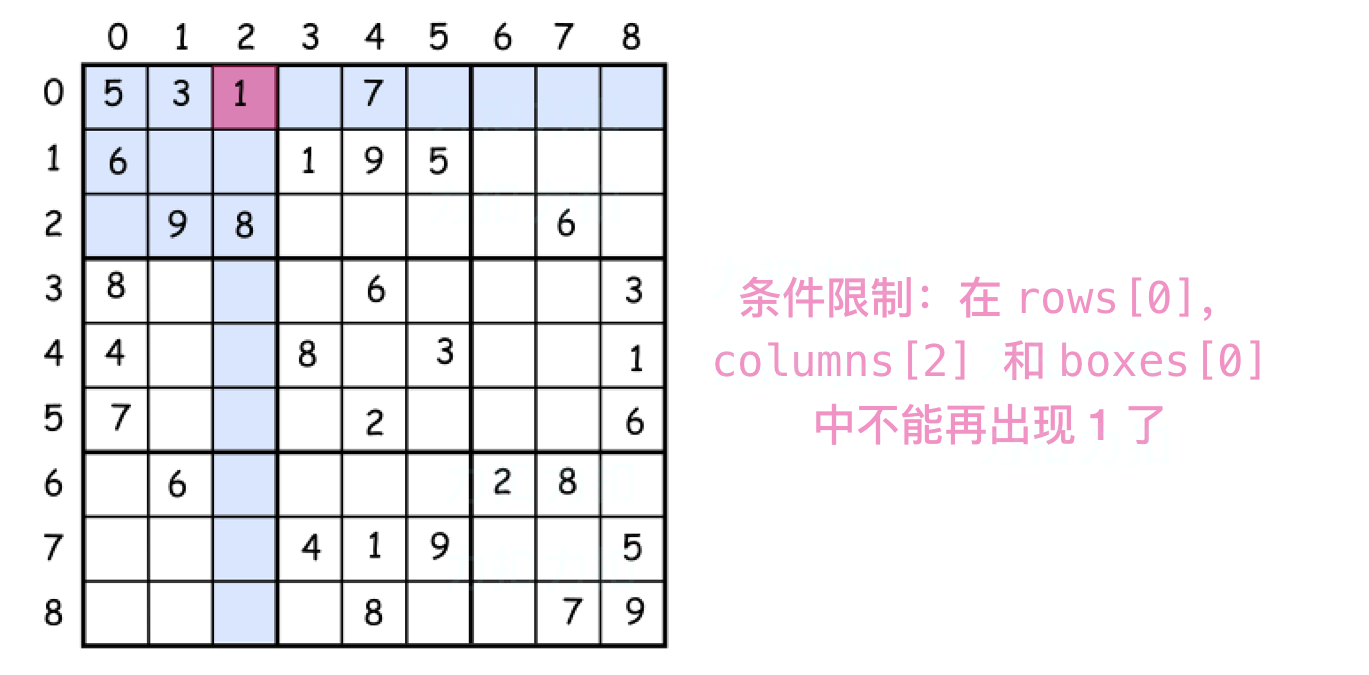
第二个叫做回溯。

让我们想象一下已经成功放置了几个数字
在数独上。
但是该组合不是最优的并且不能继续放置数字了。该怎么办？回溯。
意思是回退，来改变之前放置的数字并且继续尝试。如果还是不行，再次回溯。

技术图片

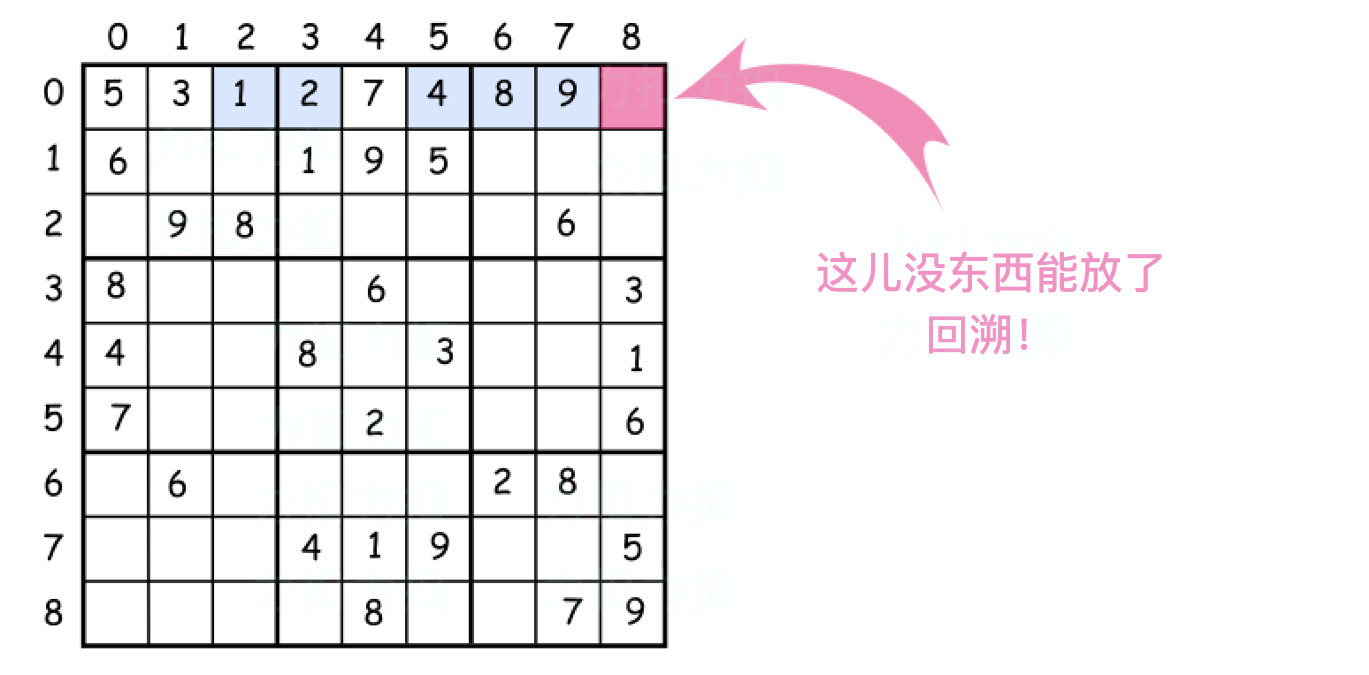
如何枚举子方块

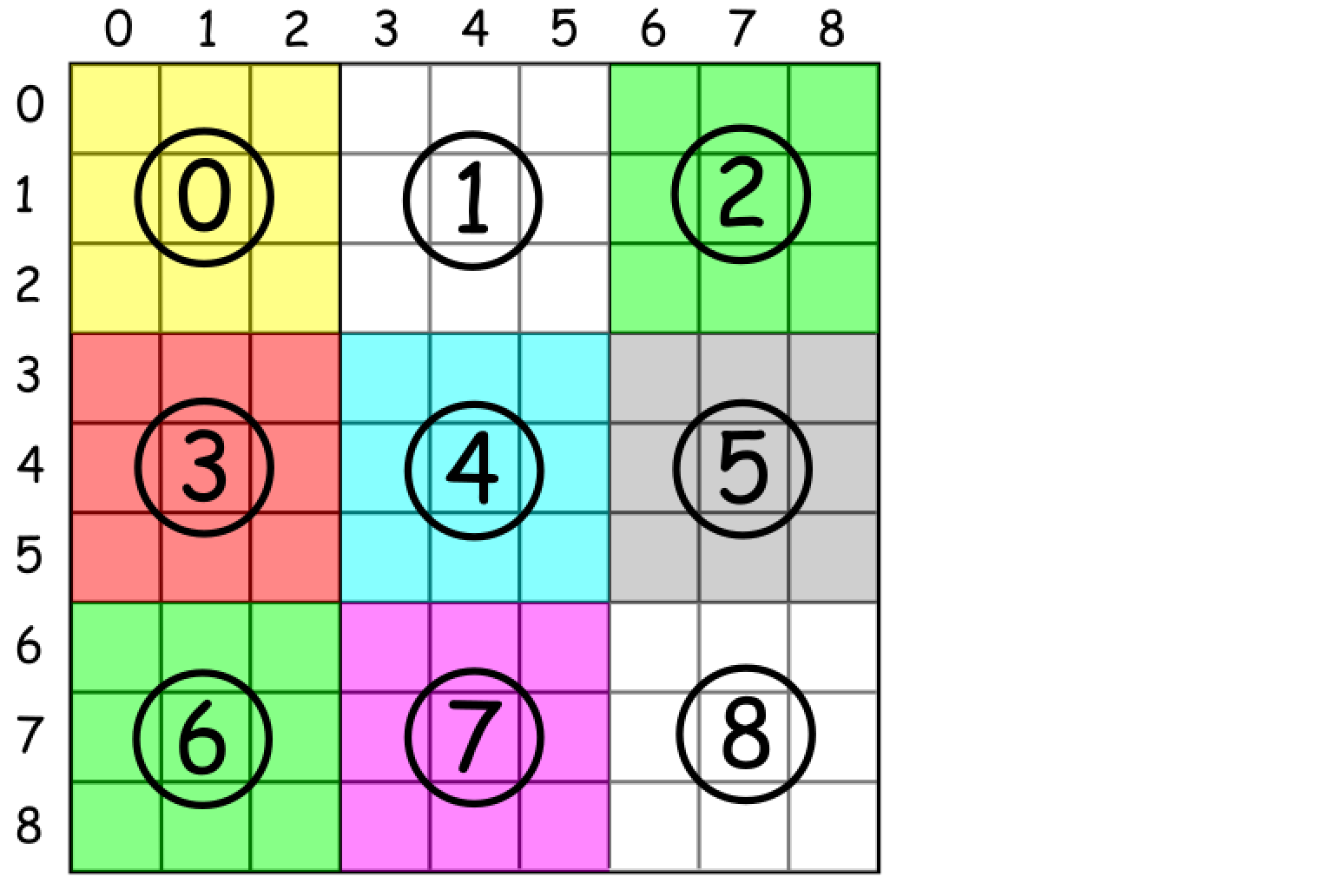
一种枚举子方块的提示是：

使用 方块索引= (行 / 3) * 3 + 列 / 3
其中 / 表示整数除法。

技术图片

算法

现在准备好写回溯函数了
backtrack(row = 0, col = 0)。

从最左上角的方格开始 row = 0, col = 0。直到到达一个空方格。
从1 到 9 迭代循环数组，尝试放置数字 d 进入 (row, col) 的格子。
- 如果数字 d 还没有出现在当前行，列和子方块中：
  - 将 d 放入 (row, col) 格子中。
  - 记录下 d 已经出现在当前行，列和子方块中。
  - 如果这是最后一个格子row == 8, col == 8 ：
    - 意味着已经找出了数独的解。
  - 否则
    - 放置接下来的数字。
  - 如果数独的解还没找到：
    将最后的数从 (row, col) 移除。

代码

Java
Python

class Solution {
  // box size
  int n = 3;
  // row size
  int N = n * n;
int [][] rows = new int[N][N + 1];

int [][] columns = new int[N][N + 1];

int [][] boxes = new int[N][N + 1];
char[][] board;
boolean sudokuSolved = false;
public boolean couldPlace(int d, int row, int col) {

/*

Check if one could place a number d in (row, col) cell

*/

int idx = (row / n ) * n + col / n;

return rows[row][d] + columns[col][d] + boxes[idx][d] == 0;

}
public void placeNumber(int d, int row, int col) {

/*

Place a number d in (row, col) cell

*/

int idx = (row / n ) * n + col / n;
rows[row][d]++;
columns[col][d]++;
boxes[idx][d]++;
board[row][col] = (<span class="hljs-keyword">char</span>)(d + <span class="hljs-string">‘0‘</span>);

}
public void removeNumber(int d, int row, int col) {

/*

Remove a number which didn‘t lead to a solution

*/

int idx = (row / n ) * n + col / n;

rows[row][d]--;

columns[col][d]--;

boxes[idx][d]--;

board[row][col] = ‘.‘;

}
public void placeNextNumbers(int row, int col) {

/*

Call backtrack function in recursion

to continue to place numbers

till the moment we have a solution

*/

// if we‘re in the last cell

// that means we have the solution

if ((col == N - 1) && (row == N - 1)) {

sudokuSolved = true;

}

// if not yet

else {

// if we‘re in the end of the row

// go to the next row

if (col == N - 1) backtrack(row + 1, 0);

// go to the next column

else backtrack(row, col + 1);

}

}
public void backtrack(int row, int col) {

/*

Backtracking

*/

// if the cell is empty

if (board[row][col] == ‘.‘) {

// iterate over all numbers from 1 to 9

for (int d = 1; d < 10; d++) {

if (couldPlace(d, row, col)) {

placeNumber(d, row, col);

placeNextNumbers(row, col);

// if sudoku is solved, there is no need to backtrack

// since the single unique solution is promised

if (!sudokuSolved) removeNumber(d, row, col);

}

}

}

else placeNextNumbers(row, col);

}
public void solveSudoku(char[][] board) {

this.board = board;
<span class="hljs-comment">// init rows, columns and boxes</span>
<span class="hljs-keyword">for</span> (<span class="hljs-keyword">int</span> i = <span class="hljs-number">0</span>; i &lt; N; i++) {
  <span class="hljs-keyword">for</span> (<span class="hljs-keyword">int</span> j = <span class="hljs-number">0</span>; j &lt; N; j++) {
    <span class="hljs-keyword">char</span> num = board[i][j];
    <span class="hljs-keyword">if</span> (num != <span class="hljs-string">‘.‘</span>) {
      <span class="hljs-keyword">int</span> d = Character.getNumericValue(num);
      placeNumber(d, i, j);
    }
  }
}
backtrack(<span class="hljs-number">0</span>, <span class="hljs-number">0</span>);

}

}

from collections import defaultdict

class Solution:

def solveSudoku(self, board):

"""

:type board: List[List[str]]

:rtype: void Do not return anything, modify board in-place instead.

"""

def could_place(d, row, col):

"""

Check if one could place a number d in (row, col) cell

"""

return not (d in rows[row] or d in columns[col] or 

d in boxes[box_index(row, col)])
    <span class="hljs-function"><span class="hljs-keyword">def</span> <span class="hljs-title">place_number</span><span class="hljs-params">(d, row, col)</span>:</span>
        <span class="hljs-string">"""
        Place a number d in (row, col) cell
        """</span>
        rows[row][d] += <span class="hljs-number">1</span>
        columns[col][d] += <span class="hljs-number">1</span>
        boxes[box_index(row, col)][d] += <span class="hljs-number">1</span>
        board[row][col] = str(d)
        
    <span class="hljs-function"><span class="hljs-keyword">def</span> <span class="hljs-title">remove_number</span><span class="hljs-params">(d, row, col)</span>:</span>
        <span class="hljs-string">"""
        Remove a number which didn‘t lead 
        to a solution
        """</span>
        <span class="hljs-keyword">del</span> rows[row][d]
        <span class="hljs-keyword">del</span> columns[col][d]
        <span class="hljs-keyword">del</span> boxes[box_index(row, col)][d]
        board[row][col] = <span class="hljs-string">‘.‘</span>    
        
    <span class="hljs-function"><span class="hljs-keyword">def</span> <span class="hljs-title">place_next_numbers</span><span class="hljs-params">(row, col)</span>:</span>
        <span class="hljs-string">"""
        Call backtrack function in recursion
        to continue to place numbers
        till the moment we have a solution
        """</span>
        <span class="hljs-comment"># if we‘re in the last cell</span>
        <span class="hljs-comment"># that means we have the solution</span>
        <span class="hljs-keyword">if</span> col == N - <span class="hljs-number">1</span> <span class="hljs-keyword">and</span> row == N - <span class="hljs-number">1</span>:
            <span class="hljs-keyword">nonlocal</span> sudoku_solved
            sudoku_solved = <span class="hljs-literal">True</span>
        <span class="hljs-comment">#if not yet    </span>
        <span class="hljs-keyword">else</span>:
            <span class="hljs-comment"># if we‘re in the end of the row</span>
            <span class="hljs-comment"># go to the next row</span>
            <span class="hljs-keyword">if</span> col == N - <span class="hljs-number">1</span>:
                backtrack(row + <span class="hljs-number">1</span>, <span class="hljs-number">0</span>)
            <span class="hljs-comment"># go to the next column</span>
            <span class="hljs-keyword">else</span>:
                backtrack(row, col + <span class="hljs-number">1</span>)
            
            
    <span class="hljs-function"><span class="hljs-keyword">def</span> <span class="hljs-title">backtrack</span><span class="hljs-params">(row = <span class="hljs-number">0</span>, col = <span class="hljs-number">0</span>)</span>:</span>
        <span class="hljs-string">"""
        Backtracking
        """</span>
        <span class="hljs-comment"># if the cell is empty</span>
        <span class="hljs-keyword">if</span> board[row][col] == <span class="hljs-string">‘.‘</span>:
            <span class="hljs-comment"># iterate over all numbers from 1 to 9</span>
            <span class="hljs-keyword">for</span> d <span class="hljs-keyword">in</span> range(<span class="hljs-number">1</span>, <span class="hljs-number">10</span>):
                <span class="hljs-keyword">if</span> could_place(d, row, col):
                    place_number(d, row, col)
                    place_next_numbers(row, col)
                    <span class="hljs-comment"># if sudoku is solved, there is no need to backtrack</span>
                    <span class="hljs-comment"># since the single unique solution is promised</span>
                    <span class="hljs-keyword">if</span> <span class="hljs-keyword">not</span> sudoku_solved:
                        remove_number(d, row, col)
        <span class="hljs-keyword">else</span>:
            place_next_numbers(row, col)
                
    <span class="hljs-comment"># box size</span>
    n = <span class="hljs-number">3</span>
    <span class="hljs-comment"># row size</span>
    N = n * n
    <span class="hljs-comment"># lambda function to compute box index</span>
    box_index = <span class="hljs-keyword">lambda</span> row, col: (row // n ) * n + col // n
    
    <span class="hljs-comment"># init rows, columns and boxes</span>
    rows = [defaultdict(int) <span class="hljs-keyword">for</span> i <span class="hljs-keyword">in</span> range(N)]
    columns = [defaultdict(int) <span class="hljs-keyword">for</span> i <span class="hljs-keyword">in</span> range(N)]
    boxes = [defaultdict(int) <span class="hljs-keyword">for</span> i <span class="hljs-keyword">in</span> range(N)]
    <span class="hljs-keyword">for</span> i <span class="hljs-keyword">in</span> range(N):
        <span class="hljs-keyword">for</span> j <span class="hljs-keyword">in</span> range(N):
            <span class="hljs-keyword">if</span> board[i][j] != <span class="hljs-string">‘.‘</span>: 
                d = int(board[i][j])
                place_number(d, i, j)
    
    sudoku_solved = <span class="hljs-literal">False</span>
    backtrack()

复杂性分析

这里的时间复杂性是常数由于数独的大小是固定的，因此没有 N 变量来衡量。
但是我们可以计算需要操作的次数： $(9!)^9$ 。
我们考虑一行，即不多于 $9$ 个格子需要填。
第一个格子的数字不会多于 $9$ 种情况，
两个格子不会多于 $9 \times 8$ 种情况，
三个格子不会多于 $9 \times 8 \times 7$ 种情况等等。
总之一行可能的情况不会多于 $9!$ 种可能，
所有行不会多于 $(9!)^9$ 种情况。比较一下：
- $9^{81}$ = 196627050475552913618075908526912116283103450944214766927315415537966391196809
  为蛮力法，
- 而 $(9!)^{9}$ = 109110688415571316480344899355894085582848000000000
  为回溯法，
  即数字的操作次数减少了 $10^{27}$ 倍！
空间复杂性：数独大小固定，空间用来存储数独，行，列和子方块的结构，每个有 81 个元素。

https://www.jianshu.com/p/c6d055a2ab64

leetcode题解之37. 解数独

标签：算法 tin adc 次数 ber ISE elements 程序提示

原文地址：https://www.cnblogs.com/leetcodetijie/p/13200373.html

踩

(0)

评论一句话评论（0）