标签:基础 题目 维数 递归调用 简单 查找树 通过 哈希树 编码
背景
如果前人认为这个一种学习提高或者检验能力的成功实践。而自己目前又没有更好的方法,那就不妨试一试。
而不管作为面试官还是被面试者,编码题最近越来越流行。而两种角色都需要思考的问题是希望考察什么能力,通过什么题目,需要达到怎样的程度可以说明面试者具有了这样的能力。
而要找到上面这些问题的答案,比较好的方式除了看一些理论性文章和接受培训之外,自己动手刷一刷leetcode切身实践一下不失为一个不错的方式。而既然要花精力去做这件事情,那就需要解决一个问题:我从中可以获得什么提高。以下是个人的一些经验和感受。
收益
对底层有了更深入的了解和思考
leetcode一些常见题也是平时工作中常用的一些底层数据结构的实现方法。
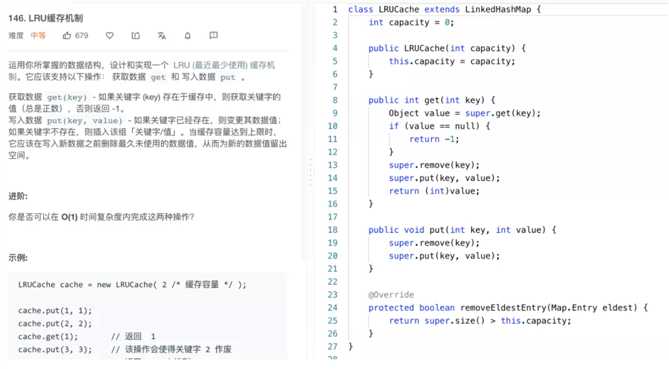
先举个大家使用比较多的算法:LRU(最近最少使用),在Java的实现中实现特别简单。只是使用了LinkedHashMap这种数据结构。而如果看一些开源包里LRU的实现,发现也是这样实现的。实际上动手实现一遍,LRU就再也不会忘了。
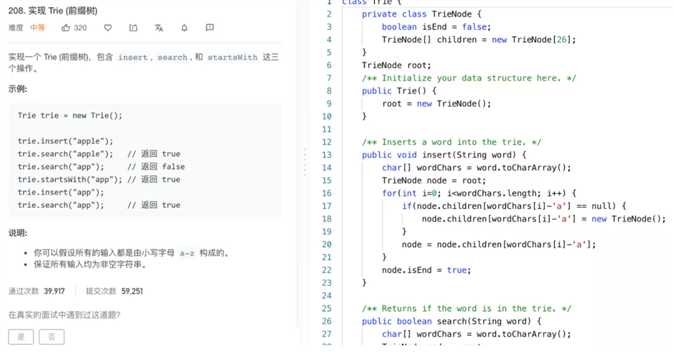
再举个数据结构的例子:字典树又叫前缀树。它是搜索和推荐的基础。标准点的定义是:
字典树又称单词查找树,Tire树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希树高。
因为之前做过搜索引擎,一直也对这块很有兴趣,所以对它底层知识的补充对个人而言,感觉深度有增加。
养成评估时空开销的习惯
我刷leetcode必看官方解答里估算的时间和空间复杂度。这也是作为一个架构师的必备基本能力。
数组、哈希这些因为数据的位置不需要进行查找,只需要算数计算就可以得到,所以它们的时间复杂度是O(1)。
链表如果直接在头部或者尾部插入,因为不需要查找,所以时间复杂度也是O(1),但是定位的话因为涉及查找,按遍历查找来算是log(n)。所以对于jdk1.7之前,hashmap底层采用的是数组+链表的数据结构。所以如果不算哈希冲突和扩容的话,获取和插入数据的时间复杂度是O(1);如果出现了哈希冲突,则插入因为是头部插入,时间复杂度还是O(1);获取时间复杂度因为涉及先查找,所以是O(n),这个n代表冲突的数量。
对于在有序数据中进行查找,因为可采用二分查找等优化,时间复杂度可降到log(n).
对于递归调用,如果递归方法内进行2次调用。对于层数n来说,时间复杂度是2的n次方。举个例子就是一个数等于前面两个数之和。当然,如果是前面3个数之和,不进行优化的情况下时间复杂度就是3的n次方。
对于一个n*m的二维数组等需要进行嵌套循环遍历的,时间复杂度是O(n*m),有个特殊情况是n*m,这时候时间复杂度是n的平方。
对于全排列的情况,时间复杂度是O(n!)。
代码简化的方法
我习惯的一种学习方法是先做题,有了一定自己的总结和思考之后,再看书学习别人的总结思考方法。对于刷leetcode相关性高,也比较受认可的书是《Cracking the Coding interview(6th)》,中文版翻译是《程序员面试金典》。这本书对于面试官和面试者来说读了都会有一定的收获。
我读了这本书,对我印象最深的是介绍了两种代码优化的方法:BUD和BCR。
BUD
BUD是瓶颈、不必要工作、重复工作 三个词组首字母的缩写。

作者提出拿到一道编程题,可先尝试用暴力解法将题目写出来,之后找到解法的性能瓶颈,针对瓶颈进行优化,之后在去掉不必要的工作,最后去掉重复的工作。
这个经典的编程优化方法不只可应用于编程,还可应用于整个程序的优化,也是最常规的优化方法。
BCR
BCR是Best Conceivable Runtime的缩写,意思是想知道自己可以优化到什么程度,先估算可达到的最优情况。
比如:在一个无序数组中,查找两个两个相同的数。直觉来说如果找到这两个数,最起码需要将每个数都遍历一遍,所以可达到的最优情况是O(n),无论怎么优化,都不可能比这个更好。所以这就是优化的上限。
这本书里还介绍了其他的优化方法如:使用额外数据结构、通过构建测试用例、根据题目的限制和提示来寻找线索,大家看这本书的时候可以了解下。
标签:基础 题目 维数 递归调用 简单 查找树 通过 哈希树 编码
原文地址:https://www.cnblogs.com/xiexj/p/13200128.html