P1186 玛丽卡

标签：起点   情况下   name   第一个   图片   const   枚举   ems   while   

题目非常得不简洁，所以这里还是做一下翻译吧

总的来说，就是给你一个图，有一些无向边，然后有一条边可能会堵车（可以理解为这条路不能走），这条边是任意的。求一个时间，这个时间满足在任意一条路堵车的时候，玛丽卡都可以从起点走到终点

那其实不难发现，这道题的答案就是在少一条边的情况下，求出所有最短路中最长的一条，这其实很好实现，枚举每一条边，使这一条边拥堵，其他边仍然联通，跑最短路，存储答案后再从所有最短路中选一条最大的就行了。到此就可以写出第一个程序（emmm..我这个FW连这个暴力都只有30，他们都有50...）

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e7+50;
const int INF=20040915;
int n,m;
struct node{
	int x,y,z;
}a[MAXN];
int head[MAXN],tot;
struct edge{
	int net,to,w;
}e[MAXN];
void add(int u,int v,int w){
	e[++tot].net=head[u];
	e[tot].to=v;
	e[tot].w=w;
	head[u]=tot;
}
bool v[MAXN];
int d[MAXN],sum,ans[MAXN];
void dij(int s){
	priority_queue<pair<int,int> > q;
	for(register int i=1;i<=n;i++){
		d[i]=INF;
		v[i]=false;
	} 
	d[s]=0;
	q.push(make_pair(0,s));
	while(!q.empty()){
		int x=q.top().second;
		q.pop();
		if(v[x]==true) continue;
		v[x]=true;
		for(register int i=head[x];i;i=e[i].net){
			int y=e[i].to,z=e[i].w;
			if(d[y]>d[x]+z){
				d[y]=d[x]+z;
				q.push(make_pair(-d[y],y));
			}
		}
	}
}
int main(){
	scanf("%d%d",&n,&m);
	for(register int i=1;i<=m;i++) scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].z);
	for(register int i=1;i<=m;i++){ //枚举任意一条边拥堵的情况 
		memset(e,0,sizeof e); //记得清零 
		for(register int j=1;j<=m;j++){ //让其他边正常连通 
			if(i!=j){
				add(a[j].x,a[j].y,a[j].z);
				add(a[j].y,a[j].x,a[j].z); //双向边 
			}
		}
		dij(1);
		ans[++sum]=d[n]; //记录答案 
	}
	int res=-INF;
	for(register int i=1;i<=sum;i++){
		res=max(res,ans[i]);
	}
	cout<<res;
	return 0;
}

好了，意料之中的超时了。如果要优化，肯定是因为有些边没啥用，所以我们看一看样例的情况，如图（粉色的表示在所有边连通时的最短路），然后我们再来手模一下上面的程序：

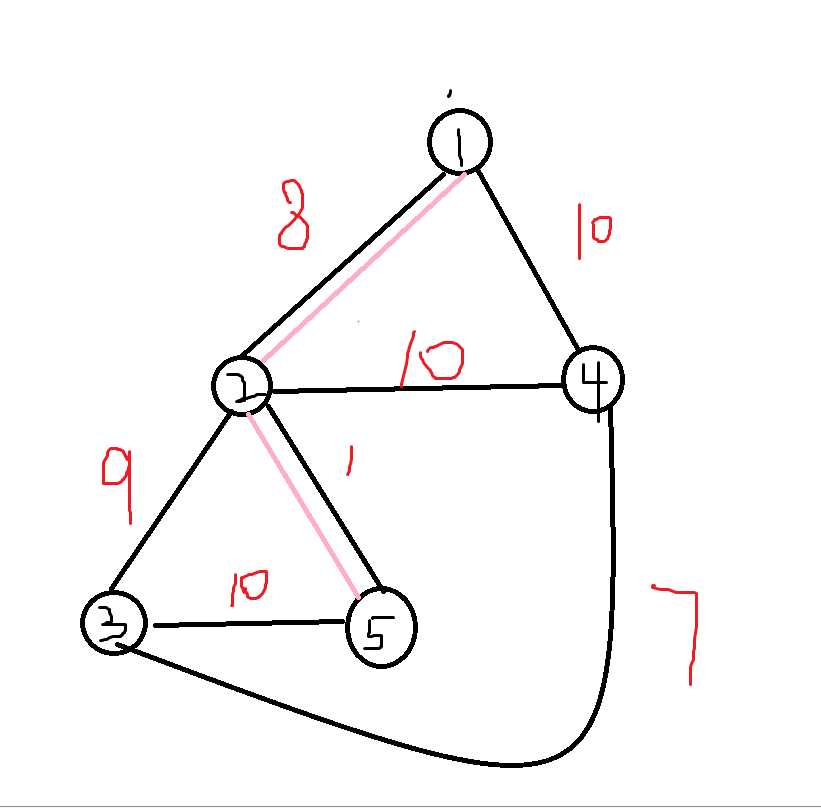
1 -> 2 (8) : 21 //改变 
1 -> 4 (10) : 9
2 -> 4 (10) : 9
2 -> 5 (1) : 27 //改变 
2 -> 3 (9) : 9
3 -> 5 (10) : 9
3 -> 4 (7) : 9

//表示在该边拥堵之后的最短路 

这么看来，答案就很显然了。当我们在改变原最短路上的任意边之后，最短路就会改变，这是很显然的，其他边的拥堵完全不会影响到原最短路。我们就可以先跑一遍最短路记录路径，然后让路径拥堵，再跑最短路就可以了

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e7+50;  //边要开两倍数组，在保证不会超出限制的情况下，多开也没什么吧 
int n,m;
struct node {
	int net,to,w,from;
} e[MAXN];
int head[MAXN],tot;
int d[MAXN],v[MAXN];
int bian[MAXN];//记录边 
void add(int u,int v,int w) {
	e[++tot].net=head[u];
	e[tot].to=v;
	e[tot].from=u;//这个用来表示前驱节点 
	e[tot].w=w;
	head[u]=tot;
}//链式前向星建边 
void dij(int s,int p) {//第一个参数表示起点，第二个参数表示哪一条边拥堵 
	priority_queue<pair<int,int> >q;
	for(register int i=1; i<=n; i++) d[i]=20040915,v[i]=false; //初始化，memset谨慎使用 
	d[s]=0;
	q.push(make_pair(0,s));
	while(!q.empty()) {
		int x=q.top().second;
		q.pop();
		if(v[x]==true) continue;
		v[x]=true;
		for(register int i=head[x]; i; i=e[i].net) {
			if(i!=p) { //如果该边没有拥堵 
				int y=e[i].to,z=e[i].w;
				if(d[y]>d[x]+z) {
					if(p==-1) bian[y]=i; //第一次跑最短路的时候用来记录路径 
					d[y]=d[x]+z;
					q.push(make_pair(-d[y],y));
				}
			}

		}
	}
}
int Max(int x,int y){
	if(x>=y) return x;
	return y;
}//手打max有些时候会快些（亲身经历） 
int main() {
	scanf("%d%d",&n,&m);
	for(register int i=1; i<=m; i++) {
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		add(u,v,w);
		add(v,u,w);
	}//输入，建双向边 
	dij(1,-1);//第一次跑最短路没有边拥堵 
	int ans=d[n],t=n; 
	while(t){ //枚举最短路上的每一条边，然后更新答案 
		dij(1,bian[t]); 
		ans=Max(ans,d[n]);
		t=e[bian[t]].from;
	}
	printf("%d",ans);
	return 0;
}

P1186 玛丽卡

标签：起点   情况下   name   第一个   图片   const   枚举   ems   while   

原文地址：https://www.cnblogs.com/Poetic-Rain/p/13207864.html