7.1集训模拟赛5（......）

时间：2020-07-01 22:30:56 阅读：65 评论：0 收藏：0 [点我收藏+]

标签：time 面积 ace scan 取数答案 block 表示最小

输入二个正整数x0,y0(2<=x0<100000,2<=y0<=1000000),求出满足下列条件的P,Q的个数

条件:

P,Q是正整数
要求P,Q以x0为最大公约数,以y0为最小公倍数.

试求:满足条件的所有可能的两个正整数的个数.

一行，二个正整数x0,y0。

一行，即满足条件的所有可能的两个正整数的个数。保证答案不需要高精度。

样例输入：

3 60

样例输出：

设有N*N的方格图(N<=20,我们将其中的某些方格中填入正整数,而其他的方格中则放入数字0。如下图所示(见样例)：

技术图片

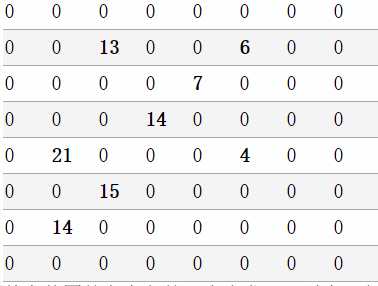
某人从图的左上角的A(1,1) 点出发，可以向下行走，也可以向右走，直到到达右下角的B(n,n)点。在走过的路上（包括起点在内），他可以取走方格中的数(取走后的方格中将变为数字0)。此人从A点到B 点共走两次，试找出2条这样的路径，使得取得的数之和为最大。

输入的第一行为一个整数N(表示N*N的方格图)

接下来的每行有三个整数，前两个表示位置，第三个数为该位置上所放的数。一行单独的0表示输入结束。

只需输出一个整数，表示2条路径上取得的最大的和。

样例输入：

样例输出：

#include<bits/stdc++.h>
using namespace std;
const int N=25;
int f[N][N][N][N],a[N][N];
int n,x,y,w;
int main(){
    scanf("%d",&n);
    while(scanf("%d%d%d",&x,&y,&w)){
        if(x==0)break;
        a[x][y]=w;
    }
    f[1][1][1][1]=a[1][1];
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            for(int k=1;k<=n;k++){
                for(int l=1;l<=n;l++){
                    if(i==k&&j==l){
                        f[i][j][k][l]=max(max(f[i-1][j][k-1][l],f[i][j-1][k-1][l]),max(f[i][j-1][k][l-1],f[i-1][j][k][l-1]))+a[k][l];
                    } else {
                        f[i][j][k][l]=max(max(f[i-1][j][k-1][l],f[i][j-1][k-1][l]),max(f[i][j-1][k][l-1],f[i-1][j][k][l-1]))+a[i][j]+a[k][l];
                    }
                }
            }
        }
    }
    printf("%d",f[n][n][n][n]);
    return 0;
}

WYT有一把巨大的刷子，刷子的宽度为M米，现在WYT要使用这把大刷子去粉刷有N列的栅栏（每列宽度都为1米；每列的高度单位也为米，由输入数据给出）。

使用刷子的规则是：

与地面垂直，从栅栏的底部向上刷
每次刷的宽度为M米（当剩余栅栏宽度不够M米的话，刷子也可以使用，具体看样例2）
对于连续的M列栅栏，刷子从底向上，刷到的高度只能到这M列栅栏的最低高度。

WYT请你回答两个问题：

最少有多少个单位面积不能刷到（单位面积为1平米）
在满足第一问的条件下，最少刷几次？

输入格式：

共两行：

第一行两个整数N和M。

第二行共N个整数，表示N列栅栏的高度。

一行，两个整数，分别为最少剩余的单位面积数量和最少刷的次数。

样例输入1：

5 3
5 3 4 4 5

样例输出1:

3
2

样例输入2:

10 3
3 3 3 3 3 3 3 3 3 3

样例输出2:

0
4

样例输入3:

7 4
1 2 3 4 3 2 1

样例输出3:

4
4

样例1的解释：

技术图片

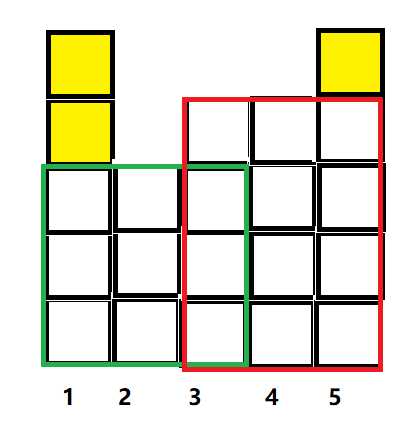
高度分别为 5 3 4 4 5 如上：

黄色的方块表示共有3个单位面积没刷上

绿色的框和红色的框表示一共刷了两次。

30%的数据：N<=10^3

50%的数据：N<=10^5

100%的数据：1<=N<=10^6, 1<=M<=10^6,N>=M, 每列栅栏的高度<=10^6.

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
typedef long long ll;
ll n,m;
ll a[N];
ll q[N];
ll j[N];
ll maxh[N],l[N],r[N];
ll sum;
int main(){
    scanf("%lld%lld",&n,&m);
    for(int i=1;i<=n;i++){
        scanf("%lld",&a[i]);
        sum+=a[i];
    }
    int head=0,tail=-1;
    for(int i=1;i<=n+1;i++){
        while(head<=tail&&a[i]<a[q[tail]]){
            r[q[tail]]=i-q[tail];
            tail--;
        }
        q[++tail]=i;
    }
    head=0;tail=-1;
    for(int i=n;i>=0;i--){
        while(head<=tail&&a[i]<a[q[tail]]){
            l[q[tail]]=q[tail]-i;
            tail--;
        }
        q[++tail]=i;
    }
    for(int i=1;i<=n;i++){
        if(l[i]+r[i]-1>=m)j[i]=1;
    }
    for(int i=1;i<=n;i++){
        if(j[i]==1){
            maxh[i]=a[i];
        } else {
            maxh[i]=maxh[i-1];
        }
    }
    for(int i=n;i>=1;i--){
        if(!j[i]){
            maxh[i]=max(maxh[i],maxh[i+1]);
        }
        sum-=maxh[i];
    }
    ll k=2,ans=0;
    while(k<=n+1){
        int cnt=1;
        while(k<=n+1&&maxh[k]==maxh[k-1]){
            cnt++;
            k++;
        }
        ans+=cnt/m;
        if(cnt%m!=0)ans++;
        k++;
    }
    printf("%lld\n%lld",sum,ans);
    return 0;
}

2017共有N棵树从0到N-1标号。现要把这些树种在一条直线上，第i棵树的种植位置X[i]如下确定：

X[0] = X[0] MOD L；

X[i] = (X[i-1]*A+B) MOD L。

每棵树种植的费用，是所有标号比它小的树与它的距离之和。2017请你计算各棵树的费用之积，最后对1000000007取余。

共五行：

第一行为N

第二行为L

第三行为X[0]

第四行为A

第五行为B

总费用

样例输入：

样例输出：

样例解释：

5棵树的位置分别为: 3, 4, 5, 6, 7.

费用分别为: 1, 3, 6, 10. （从第一棵树开始）

总费用为： 1 × 3 × 6 × 10 = 180.

10%的数据：N<=10;

60%的数据：N<=2×10^5;

100%的数据：N,L<=200000; X[0] ,A, B<=10^9.

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=200010;
ll n,l,x,a,b;
ll c1,c2,s1,s2;
ll cost,ans = 1;
struct edge{
    ll cnt;
    ll val;
}tree[N<<2];



void updata(int rt,int l,int r,int x,int val){
    if (l > x || r < x) return;
    if(l==r){
        tree[rt].val+=val;
        tree[rt].cnt++;
        return ;
    }
    ll mid = (l+r)>>1;
    if(x<=mid){
        updata(rt*2,l,mid,x,val);
    } else {
        updata(rt*2+1,mid+1,r,x,val);
    }
    tree[rt].cnt=tree[rt*2].cnt+tree[rt*2+1].cnt;
    tree[rt].val=tree[rt*2].val+tree[rt*2+1].val;
    //return ;
}

ll getval(int rt,int l,int r,int x,int y){
    if(y<l||x>r)return 0;
    if(x<=l&&y>=r)return tree[rt].val;
    ll mid = (l+r)>>1;
    ll sum=0;
    if(x<=mid){
        sum+=getval(rt*2,l,mid,x,y);
    }if(y>mid){
        sum+=getval(rt*2+1,mid+1,r,x,y);
    }
    return sum;
}

ll getcnt(int rt,int l,int r,int x,int y){
    if(y<l||x>r)return 0;
    if(x<=l&&y>=r)return tree[rt].cnt;
    ll mid = (l+r)>>1;
    ll sum=0;
    if(x<=mid){
        sum+=getcnt(rt*2,l,mid,x,y);
    }if(y>mid){
        sum+=getcnt(rt*2+1,mid+1,r,x,y);
    }
    return sum;
}


int main(){
    scanf("%lld%lld%lld%lld%lld",&n,&l,&x,&a,&b);
    x=x%l;
    //updata(1,1,l,x+1,x);
    for(int i=1;i<n;i++){
        updata(1,1,l,x+1,x+1);
        x=(x*a+b)%l;
        c1=getcnt(1,1,l,1,x+1);
        c2=i-c1;
        s1=getval(1,1,l,1,x+1);
        s2=tree[1].val-s1;
        cost = (c1*(x+1)-s1+s2-c2*(x+1))%1000000007;
        //printf("%lld  %lld  %lld  %lld\n",c1,c2,s1,s2);
        //printf("%lld\n",cost);
        ans = (ans*cost)%1000000007;
        //updata(1,1,l,x+1,x);
    }
    printf("%lld",ans);
    return 0;
}

#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;
typedef long long ll;
#define lson (rt << 1)
#define rson (rt << 1 | 1)
#define MAXTREE 200001

const int N = 200000 + 10;
const int MOD = 1000000007;

struct SegTree {
    ll sum;
    int cnt;
} tree[N << 2];

int n, L, a, b;
int x;
ll ans = 1;
int tot;

void pushup(int rt) {
tree[rt].sum = (tree[lson].sum + tree[rson].sum);
tree[rt].cnt = tree[lson].cnt + tree[rson].cnt;
}

void update(int rt, int L, int R, int pos, int val) {
    if (L > pos || R < pos) return;
    if (L == R) {
        tree[rt].sum = (tree[rt].sum + val);
        ++tree[rt].cnt;
        return;
    }
    int mid = (L + R) >> 1;
    if (mid < pos) update(rson, mid+1, R, pos, val);
    else update(lson, L, mid, pos, val);
    pushup(rt);
}

int qeurycnt(int rt, int L, int R, int l, int r) {
    if (L > r || R < l) return 0;
    if (l <= L && r >= R) return tree[rt].cnt;
    int mid = (L + R) >> 1;
    return qeurycnt(lson, L, mid, l, r) + qeurycnt(rson, mid + 1, R, l, r);
}

ll qeurysum(int rt, int L, int R, int l, int r) {
    if (L > r || R < l) return 0;
    if (l <= L && r >= R) return tree[rt].sum;
    int mid = (L + R) >> 1;
    return (qeurysum(lson, L, mid, l, r) + qeurysum(rson, mid + 1, R, l, r));
}

int main() {
    scanf("%d%d%d%d%d", &n, &L, &x, &a, &b);
    x = x % L;
    int c1, c2;
    ll s1, s2, sum = 0;
    for (int i = 1; i < n; ++i) {
    update(1, 1, L, x+1, x+1); // 从 1 开始
    //sum = (sum + x + 1) % MOD;
    x = ((ll)x * a % L + b) % L;
    //printf("x = %lld\n", x);

    c1 = qeurycnt(1, 1, L, 1, x+1);
    //c2 = qeurycnt(1, 1, MAXTREE, x+1, MAXTREE);
    c2 = i - c1;
    s1 = qeurysum(1, 1, L, 1, x+1);
    //s2 = qeurysum(1, 1, MAXTREE, x+1, MAXTREE);
    s2 = tree[1].sum - s1;
    printf("%d  %d  %lld  %lld\n",c1,c2,s1,s2);
    //printf("c1 = %d c2 = %d s1 = %lld s2 = %lld\n", c1, c2, s1, s2);

    ll cost = (((ll)c1 * (x+1) % MOD - s1 + s2 - (ll)c2 * (x+1) %MOD)%MOD+MOD)%MOD;
    //printf("cost = %lld\n", cost);
    ans = ans * cost % MOD;
    
    //update(1, 1, MAXTREE, x, x);
}
printf("%lld\n", ans);
return 0;
}

7.1集训模拟赛5（......）

标签：time 面积 ace scan 取数答案 block 表示最小

原文地址：https://www.cnblogs.com/LightyaChoo/p/13220898.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行

7.1集训模拟赛5（......）

A. 最大公约数和最小公倍数问题：

题目描述：

输入格式：

输出格式：

样例

样例输入：

样例输出：

B. 方格取数：

题目描述：

输入格式：

输出格式：

样例：

样例输入：

样例输出：

C. WYT的刷子：

题目描述：

输入格式：

输出格式：

样例

样例输入1：

样例输出1:

样例输入2:

样例输出2:

样例输入3:

样例输出3:

样例1的解释：

数据范围与提示：

D. 2017种树：

题目描述：

输入格式：

输出格式：

样例：

样例输入：

样例输出：

样例解释：

数据范围与提示：