标签:play int cli ++i 入门 style 情况 define color

#include<bits/stdc++.h> using namespace std; #define N 200000 + 5 #define M 1000000 + 5 #define rep(i, l, r) for(int i = l; i <= r; ++i) struct node{ int l, r, id; }q[N]; int n, l, r, ql, qr, Q, ans, size, a[N], Ans[N], cnt[M], block[N]; int read(){ char c; int x = 0, f = 1; c = getchar(); while(c > ‘9‘ || c < ‘0‘){ if(c == ‘-‘) f = -1; c = getchar();} while(c >= ‘0‘ && c <= ‘9‘) x = x * 10 + c - ‘0‘, c = getchar(); return x * f; } bool cmp(node a, node b){ return (block[a.l] ^ block[b.l]) ? a.l < b.l : ((a.l & 1) ? a.r < b.r : a.r > b.r); //奇数块右端点从小到大排序,偶数块从大到小排序,这样扫完奇数块刚好可以回来。 } int main(){ n = read(), size = sqrt(n); rep(i, 1, n) a[i] = read(), block[i] = ceil(1.0 * i / size); Q = read(); rep(i, 1, Q) q[i].l = read(), q[i].r = read(), q[i].id = i; sort(q + 1, q + Q + 1, cmp); l = 1, r = 0; rep(i, 1, Q){ ql = q[i].l, qr = q[i].r; while(l < ql) ans -= !--cnt[a[l++]]; while(l > ql) ans += !cnt[a[--l]]++; while(r > qr) ans -= !--cnt[a[r--]]; while(r < qr) ans += !cnt[a[++r]]++; //卡常写法。 Ans[q[i].id] = ans; } rep(i, 1, Q) printf("%d ", Ans[i]); return 0; }

#include<bits/stdc++.h> using namespace std; #define N 1000000 + 5 #define K 5 #define rep(i, l, r) for(int i = l; i <= r; ++i) struct R{ int pos, col; }c[N]; struct Q{ int l, r, t, id; }q[N]; char opt[K]; int n, m, l, r, t, ql, qr, qt, ans, tot1, tot2, size, a[N], cnt[N], Ans[N], block[N]; int read(){ char c; int x = 0, f = 1; c = getchar(); while(c > ‘9‘ || c < ‘0‘){ if(c == ‘-‘) f = -1; c = getchar();} while(c >= ‘0‘ && c <= ‘9‘) x = x * 10 + c - ‘0‘, c = getchar(); return x * f; } bool cmp(Q a, Q b){ return (block[a.l] ^ block[b.l]) ? a.l < b.l : ((block[a.r] ^ block[b.r]) ? a.r < b.r : a.t < b.t); } int main(){ n = read(), m = read(), size = pow(n, 1.0 * 2 / 3); rep(i, 1, n) block[i] = ceil(1.0 * i / size); rep(i, 1, n) a[i] = read(); rep(i, 1, m){ scanf("%s", opt + 1), l = read(), r = read(); if(opt[1] == ‘Q‘){ if(l > r) swap(l, r); q[++tot1].l = l, q[tot1].r = r, q[tot1].t = tot2, q[tot1].id = tot1; } else c[++tot2].pos = l, c[tot2].col = r; } sort(q + 1, q + tot1 + 1, cmp); l = 1, r = 0, t = 0; rep(i, 1, tot1){ ql = q[i].l, qr = q[i].r, qt = q[i].t; while(l < ql) ans -= !--cnt[a[l++]]; while(l > ql) ans += !cnt[a[--l]]++; while(r < qr) ans += !cnt[a[++r]]++; while(r > qr) ans -= !--cnt[a[r--]]; while(t < qt){ ++t; if(c[t].pos >= ql && c[t].pos <= qr) ans -= !--cnt[a[c[t].pos]] - !cnt[c[t].col]++; //注意这里一定要边删边统计答案,否则当前的状态不知道统计的答案是错的。 swap(a[c[t].pos], c[t].col); //这里是一种取巧的写法,这样就可以不记录每个位置应该的颜色,因为每次我们修改过去会swap一遍,修改回来也会swap一遍两次swap相当于没有修改。下同 } while(t > qt){ if(c[t].pos >= ql && c[t].pos <= qr) ans -= !--cnt[a[c[t].pos]] - !cnt[c[t].col]++; swap(a[c[t].pos], c[t].col); --t; } Ans[q[i].id] = ans; } rep(i, 1, tot1) printf("%d\n", Ans[i]); return 0; }
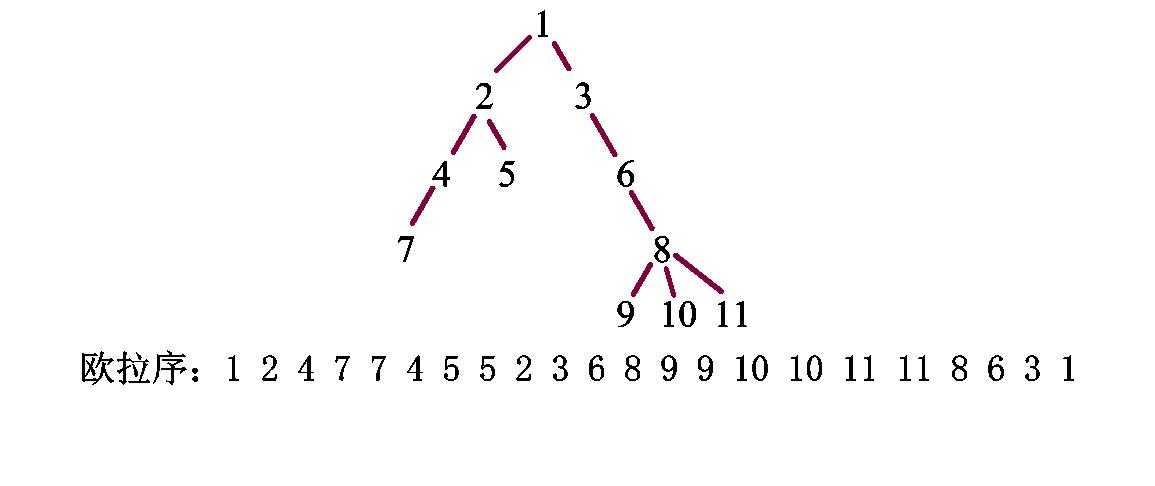
那么莫队能否像树剖那样上树呢?事实上是可以的,和树剖一样我们把树上的问题转化到序列上来。树剖使用的是 $dfs$ 序,但 $dfs$ 序不能直接表达出一段区间,于是我们考虑使用欧拉序。比如下面这张图

#include<bits/stdc++.h> using namespace std; #define N 1000000 + 5 #define rep(i, l, r) for(int i = l; i <= r; ++i) #define Next(i, u) for(int i = h[u]; i; i = e[i].next) struct node{ int l, r, lca, id; }q[N]; struct edge{ int v, next; }e[N << 1]; bool book[N]; int n, m, l, r, u, v, ql, qr, ans, tot, num, now, Lca, size; int a[N], s[N], d[N], h[N], fa[N], top[N], Ans[N], dep[N], son[N], ord[N], cnt[N], fir[N], sec[N], block[N]; int read(){ char c; int x = 0, f = 1; c = getchar(); while(c > ‘9‘ || c < ‘0‘){ if(c == ‘-‘) f = -1; c = getchar();} while(c >= ‘0‘ && c <= ‘9‘) x = x * 10 + c - ‘0‘, c = getchar(); return x * f; } bool cmp(node a, node b){ return (block[a.l] ^ block[b.l]) ? a.l < b.l : ((block[a.l] & 1) ? a.r < b.r : a.r > b.r); } void add(int u, int v){ e[++tot].v = v, e[tot].next = h[u], h[u] = tot; } void dfs1(int u, int Fa){ ord[++now] = u, fir[u] = now; fa[u] = Fa, dep[u] = dep[Fa] + 1, s[u] = 1; int Max = -1; Next(i, u){ int v = e[i].v; if(v == Fa) continue; dfs1(v, u), s[u] += s[v]; if(s[v] > Max) Max = s[v], son[u] = v; } ord[++now] = u, sec[u] = now; } void dfs2(int u, int topf){ top[u] = topf; if(!son[u]) return; dfs2(son[u], topf); Next(i, u){ int v = e[i].v; if(v == fa[u] || v == son[u]) continue; dfs2(v, v); } } int LCA(int x, int y){ while(top[x] != top[y]){ if(dep[top[x]] < dep[top[y]]) swap(x, y); x = fa[top[x]]; } return dep[x] < dep[y] ? x : y; } void solve(int pos){ book[pos] ? ans -= !--cnt[a[pos]] : ans += !cnt[a[pos]]++; book[pos] ^= 1; // book表示当前是否要对答案产生贡献,因为只有出现一次才对答案有贡献 } int main(){ n = read(), m = read(), size = sqrt(n); rep(i, 1, n) block[i] = ceil(1.0 * i / size); rep(i, 1, n) a[i] = d[i] = read(); rep(i, 1, n - 1) u = read(), v = read(), add(u, v), add(v, u); dfs1(1, 0), dfs2(1, 1); rep(i, 1, m){ u = read(), v = read(), Lca = LCA(u, v); if(fir[u] > fir[v]) swap(u, v); if(u == Lca) q[i].l = fir[u], q[i].r = fir[v], q[i].id = i; else q[i].l = sec[u], q[i].r = fir[v], q[i].lca = Lca, q[i].id = i; } sort(d + 1, d + n + 1), sort(q + 1, q + m + 1, cmp); num = unique(d + 1, d + n + 1) - d - 1; rep(i, 1, n) a[i] = lower_bound(d + 1, d + num + 1, a[i]) - d; l = 1, r = 0; rep(i, 1, m){ ql = q[i].l, qr = q[i].r, Lca = q[i].lca; while(l < ql) solve(ord[l++]); while(l > ql) solve(ord[--l]); while(r > qr) solve(ord[r--]); while(r < qr) solve(ord[++r]); if(Lca) solve(Lca); Ans[q[i].id] = ans; if(Lca) solve(Lca); } rep(i, 1, m) printf("%d\n", Ans[i]); return 0; }

#include<bits/stdc++.h> using namespace std; #define N 100000 + 5 #define rep(i, l, r) for(int i = l; i <= r; ++i) typedef long long ll; struct node{ int l, r, id; }q[N]; ll ans, Ans[N]; int n, m, l, r, j, ql, qr, tot, num, siz; int a[N], b[N], d[N], cnt[N], en[N], rcnt[N], block[N]; int read(){ char c; int x = 0, f = 1; c = getchar(); while(c > ‘9‘ || c < ‘0‘){ if(c == ‘-‘) f = -1; c = getchar();} while(c >= ‘0‘ && c <= ‘9‘) x = x * 10 + c - ‘0‘, c = getchar(); return x * f; } bool cmp(node a, node b){ return (block[a.l] ^ block[b.l]) ? a.l < b.l : a.r < b.r; } int main(){ n = read(), m = read(), siz = sqrt(n); rep(i, 1, n){ block[i] = ceil(1.0 * i / siz); if(block[i] != block[i - 1] && i != 1) en[(int)ceil(1.0 * (i - 1) / siz)] = i - 1; } tot = ceil(1.0 * n / siz), en[tot] = n; rep(i, 1, n) a[i] = b[i] = d[i] = read(); sort(d + 1, d + n + 1); num = unique(d + 1, d + n + 1) - d - 1; rep(i, 1, n) a[i] = lower_bound(d + 1, d + num + 1, a[i]) - d; rep(i, 1, m) q[i].l = read(), q[i].r = read(), q[i].id = i; sort(q + 1, q + m + 1, cmp); j = 1; rep(i, 1, tot){ l = en[i] + 1, r = en[i], ans = 0; memset(cnt, 0, sizeof(cnt)); // 记得清空数组。 for(; block[q[j].l] == i; ++j){ ql = q[j].l, qr = q[j].r; if(block[ql] == block[qr]){ rep(k, ql, qr) ++rcnt[a[k]], ans = max(ans, 1ll * b[k] * rcnt[a[k]]); Ans[q[j].id] = ans; ans = 0; rep(k, ql, qr) --rcnt[a[k]]; } else{ ll tmp; //右端点能到达的最大答案 while(r < qr) ++cnt[a[++r]], ans = max(ans, 1ll * b[r] * cnt[a[r]]); tmp = ans; while(l > ql) ++cnt[a[--l]], ans = max(ans, 1ll * b[l] * cnt[a[l]]); while(l <= en[i]) --cnt[a[l++]]; Ans[q[j].id] = ans, ans = tmp; } } } rep(i, 1, m) printf("%lld\n", Ans[i]); return 0; }
标签:play int cli ++i 入门 style 情况 define color
原文地址:https://www.cnblogs.com/Go7338395/p/13223944.html