二叉树的基本操作实现

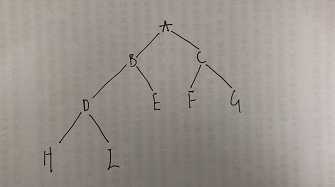
#include <iostream>
#include<string.h>
#include <stdio.h>
#include<stack>
#include<queue>
using namespace std;
typedef char ElemType;
typedef struct BiNode//二叉树结点结构定义
{
    ElemType data;//结点元素值
    struct BiNode* lchild, * rchild;//结点元素的左右孩子指针
}BiNode,*BiTree;

// 通过前序遍历法创建一棵二叉树，其形参使用结点的二级指针。当每个叶结点的左右孩子是‘#’时表示二叉树创建完成
void CreateTree(BiTree* T)
{
    char word;
    cin >> word;
    if (word == ‘#‘)
        *T = NULL;//表示结点孩子不存在
    else
    {
        *T = new BiNode();//将新创建的结点添加到树结点中
        if (!*T)
            exit(-1);
        (*T)->data = word;
        CreateTree(&(*T)->lchild);//创建结点的左子树
        CreateTree(&(*T)->rchild);//创建结点的右子树
    }
   
}

//释放二叉树空间
void DestroyTree(BiTree* T)
{
    if (*T == nullptr)
        return;
    DestroyTree(&(*T)->lchild);
    DestroyTree(&(*T)->rchild);
    delete T;
}

//递归前序遍历法：思想先根结点，在左子树最后右子树；（每个非叶子结点都可以看作临时根结点）根-左-右；
void PreOrderTarverse(BiTree T)
{
    if (T == NULL)
        return;
    cout << T->data << " ";
    PreOrderTarverse(T->lchild);
    PreOrderTarverse(T->rchild);
}
//非递归前序遍历法：思想：通过栈的先进后出属性，边进栈边打印结点数据。先将根结点及左孩子都进栈，直到左孩子为空，进栈结束
//当栈不空时，出栈，并访问出栈结点的右孩子。若右孩子不为空则继续进栈操作。
void PreOrderTarverse1(BiTree T)
{
    if (T == NULL)
        return;
    stack< BiTree>s;//栈用来存放结点指针
    BiTree p = T;
    while (p || !s.empty())
    {
        while (p)//进栈操作直到左孩子为空进栈结束
        {
            s.push(p);
            cout << p->data << " ";
            p = p->lchild;
        }
        if (!s.empty())//出栈操作
        {
            p = s.top();
            s.pop();
            p = p->rchild;
        }
    }
}

//递归中序遍历法：思想先左子树，在根结点最后右子树；（每个非叶子结点都可以看作临时根结点）左-根-右；
void InOrderTarverse(BiTree T)
{

    if (T == NULL)
        return; 
    InOrderTarverse(T->lchild);
    cout << T->data << " ";
    InOrderTarverse(T->rchild);
}
//非递归中序遍历法：思想：通过栈的先进后出属性，出栈时打印结点数据。先将根结点及左孩子都进栈，直到左孩子为空，进栈结束
//当栈不空时，出栈，并打印出栈结点数据，访问出栈结点的右孩子。若右孩子不为空则继续进栈操作。
void InOrderTarverse2(BiTree T)
{
    if (T == NULL)
        return;
    BiTree p = T;  
    stack<BiTree>s;//栈用来存放结点指针
    while (p || !s.empty())
    {
        while (p)
        {
            s.push(p);          
            p = p->lchild;
        }
        if (!s.empty())
        {
            p = s.top();
            cout << p->data << " ";
            s.pop();
            p = p->rchild;
        }
    }
}

//递归后序遍历法：思想先左子树，在右子树，最后根结点；（每个非叶子结点都可以看作临时根结点）左-右-根；
void PostOrderTarverse(BiTree T)
{
    if (T == NULL)
        return;
    PostOrderTarverse(T->lchild);
    PostOrderTarverse(T->rchild);
    cout << T->data << " ";
}
//非递归后序遍历法：思想通过双栈法实现，先根结点进栈，在右结点进栈，直到右节点为空。然后出栈并访问出栈结点的左孩子。
//若左孩子不为空继续执行进栈操作。最后将其中一个栈的元素全部出栈打印。
void PostOrderTarverse3(BiTree T)
{
    BiTree p = T;
    stack<BiTree>s1;//栈1
    stack<BiTree>s2;//栈2最后通过出栈打印结点数据
    while (p || !s1.empty())
    {
        while (p)//结点进栈操作
        {
            s1.push(p);
            s2.push(p);
            p = p->rchild;
        }
        if (!s1.empty())//结点出栈操作
        {
            p = s1.top();
            s1.pop();
            p = p->lchild;
        }
    }
    while (!s2.empty())//打印结点操作
    {
        cout << s2.top()->data << " ";
        s2.pop();
    }
}

//层序队列遍历法：通过队列的先进先出属性父类结点出队其左右孩子进队，先将根结点进队，然后出队，若出队结点的左孩子存在则左孩子进队，
//若右孩子存在则右孩子进队。然后继续出队循环执行。
void OrderTraverse(BiTree T)
{
    if (T == NULL)
        return;
    BiTree p = T;
    queue<BiTree>q;//队列
    q.push(T);//根结点入队
    while (!q.empty())
    {
        p = q.front();
        q.pop();//出队
        cout << p->data << " ";
        if (p->lchild)//左孩子入队
            q.push(p->lchild);
        if (p->rchild)//右孩子入队
            q.push(p->rchild);
    }
}

//叶子结点数
int leafTree(BiTree T)
{
    if (T == nullptr)
        return 0;
    else if (T->lchild == NULL && T->rchild == NULL)
        return 1;
    else
    {
        return (leafTree(T->lchild) + leafTree(T->rchild));
    }
}

//结点个数
int numTree(BiTree T)
{
    if (!T)
        return 0;
    else
        return 1 + numTree(T->lchild) + numTree(T->rchild);
}

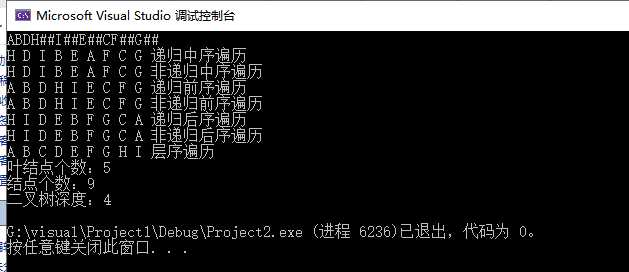
//二叉树深度
int DepthTree(BiTree T)
{
    if (!T)
        return 0;
    else
        return DepthTree(T->lchild) > DepthTree(T->rchild)
        ? DepthTree(T->lchild) + 1 : DepthTree(T->rchild) + 1;
}
int main()
{
    BiTree P = NULL;
    CreateTree(&P);
    InOrderTarverse(P);
    cout << "递归中序遍历" << endl;
    InOrderTarverse2(P);
    cout << "非递归中序遍历" << endl;
    PreOrderTarverse(P);
    cout << "递归前序遍历" << endl;
    PreOrderTarverse1(P);
    cout << "非递归前序遍历" << endl;
    PostOrderTarverse(P);
    cout << "递归后序遍历" << endl;
    PostOrderTarverse3(P);  
    cout << "非递归后序遍历" << endl;
    OrderTraverse(P);
    cout << "层序遍历" << endl;
    cout << "叶结点个数：" << leafTree(P)<< endl;
    cout << "结点个数：" << numTree(P) << endl;
    cout << "二叉树深度：" << DepthTree(P) << endl;
    return 0;
}