循环序列模型-week1编程题1（一步步搭建循环神经网络）

 1 import numpy as np
 2 from rnn_utils import *
 3 
 4 #单步前向传播
 5 def rnn_cell_forward(xt, a_prev, parameters):
 6     """
 7     Implements a single forward step of the RNN-cell as described in Figure (2)
 8 
 9     Arguments:
10     xt -- your input data at timestep "t", numpy array of shape (n_x, m).
11     a_prev -- Hidden state at timestep "t-1", numpy array of shape (n_a, m)
12     parameters -- python dictionary containing:
13                         Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
14                         Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
15                         Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
16                         ba --  Bias, numpy array of shape (n_a, 1)
17                         by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
18     Returns:
19     a_next -- next hidden state, of shape (n_a, m)
20     yt_pred -- prediction at timestep "t", numpy array of shape (n_y, m)
21     cache -- tuple of values needed for the backward pass, contains (a_next, a_prev, xt, parameters)
22     """
23     # Retrieve parameters from "parameters"
24     Wax = parameters["Wax"]
25     Waa = parameters["Waa"]
26     Wya = parameters["Wya"]
27     ba = parameters["ba"]
28     by = parameters["by"]
29     
30     ### START CODE HERE ### (≈2 lines)
31     # compute next activation state using the formula given above
32     a_next = np.tanh(np.dot(Waa, a_prev) + np.dot(Wax, xt) + ba)
33     # compute output of the current cell using the formula given above
34     yt_pred = softmax(np.dot(Wya, a_next) + by)
35     ### END CODE HERE ###
36     
37     # store values you need for backward propagation in cache
38     cache = (a_next, a_prev, xt, parameters)   
39     return a_next, yt_pred, cache

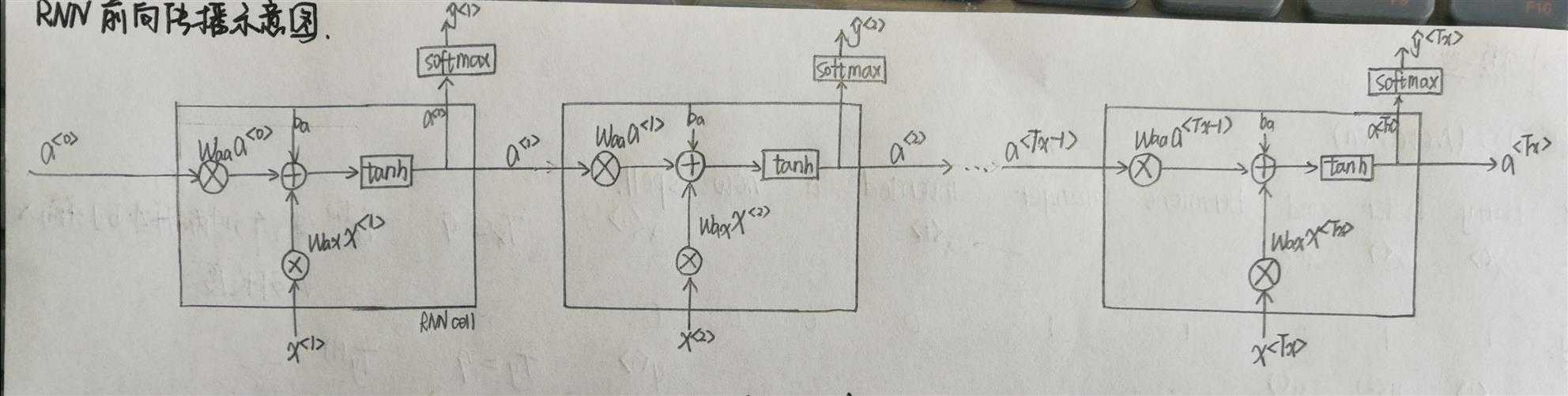
 1 def rnn_forward(x, a0, parameters):
 2     """
 3     Implement the forward propagation of the recurrent neural network described in Figure (3).
 4 
 5     Arguments:
 6     x -- Input data for every time-step, of shape (n_x, m, T_x).
 7     a0 -- Initial hidden state, of shape (n_a, m)
 8     parameters -- python dictionary containing:
 9                         Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
10                         Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
11                         Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
12                         ba --  Bias numpy array of shape (n_a, 1)
13                         by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
14 
15     Returns:
16     a -- Hidden states for every time-step, numpy array of shape (n_a, m, T_x)
17     y_pred -- Predictions for every time-step, numpy array of shape (n_y, m, T_x)
18     caches -- tuple of values needed for the backward pass, contains (list of caches, x)
19     """
20     # Initialize "caches" which will contain the list of all caches
21     caches = []
22     
23     # Retrieve dimensions from shapes of x and Wy
24     n_x, m, T_x = x.shape
25     n_y, n_a = parameters["Wya"].shape
26     
27     ### START CODE HERE ### 
28     # initialize "a" and "y" with zeros (≈2 lines)
29     a=np.zeros((n_a,m,T_x))
30     y_pred=np.zeros((n_y,m,T_x))
31     
32     # Initialize a_next (≈1 line)
33     a_next=a0 
34     
35     # loop over all time-steps
36     for t in range(T_x):
37         # Update next hidden state, compute the prediction, get the cache (≈1 line)
38         a_next, yt_pred, cache=rnn_cell_forward(x[:,:,t], a_next, parameters)
39         # Save the value of the new "next" hidden state in a (≈1 line)
40         a[:,:,t]=a_next
41         # Save the value of the prediction in y (≈1 line)
42         y_pred[:,:,t]=yt_pred
43         # Append "cache" to "caches" (≈1 line)
44         caches.append(cache)        
45     ### END CODE HERE ###
46         
47     # store values needed for backward propagation in cache
48     caches = (caches, x)
49     return a, y_pred, caches

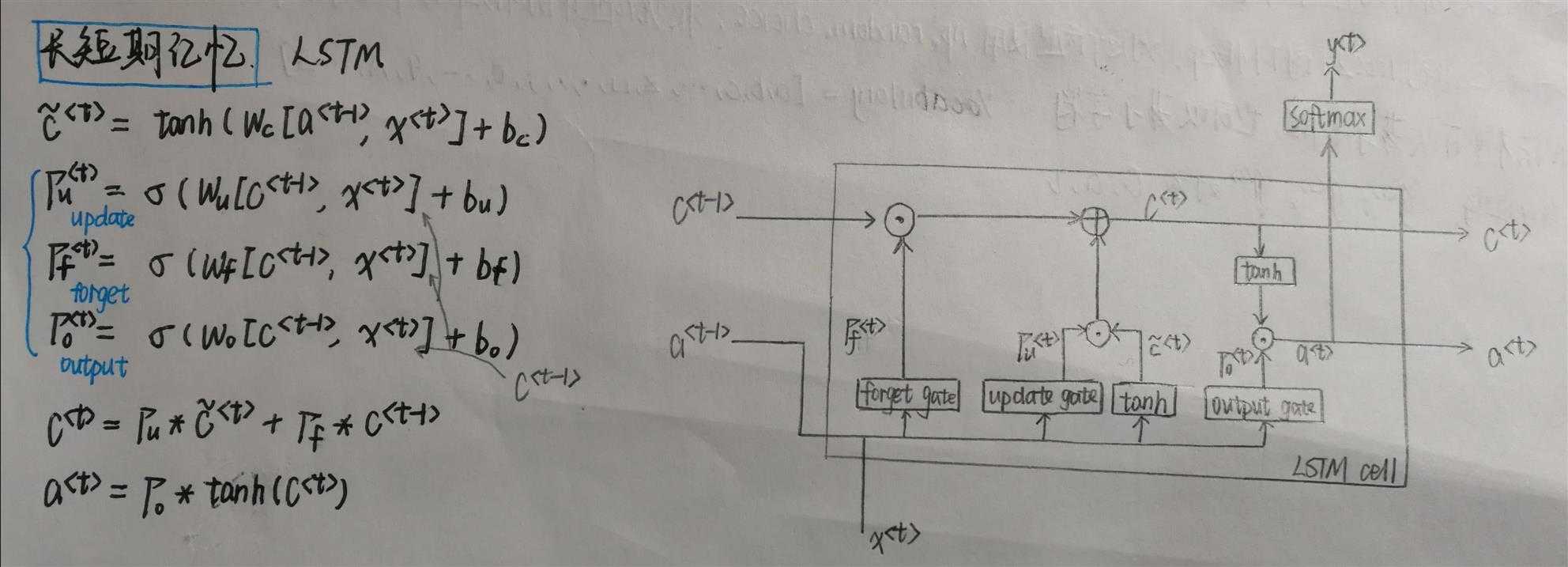
 1 def lstm_cell_forward(xt, a_prev, c_prev, parameters):
 2     """
 3     Implement a single forward step of the LSTM-cell as described in Figure (4)
 4 
 5     Arguments:
 6     xt -- your input data at timestep "t", numpy array of shape (n_x, m).
 7     a_prev -- Hidden state at timestep "t-1", numpy array of shape (n_a, m)
 8     c_prev -- Memory state at timestep "t-1", numpy array of shape (n_a, m)
 9     parameters -- python dictionary containing:
10                         Wf -- Weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
11                         bf -- Bias of the forget gate, numpy array of shape (n_a, 1)
12                         Wi -- Weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)
13                         bi -- Bias of the update gate, numpy array of shape (n_a, 1)
14                         Wc -- Weight matrix of the first "tanh", numpy array of shape (n_a, n_a + n_x)
15                         bc --  Bias of the first "tanh", numpy array of shape (n_a, 1)
16                         Wo -- Weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x)
17                         bo --  Bias of the output gate, numpy array of shape (n_a, 1)
18                         Wy -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
19                         by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
20                         
21     Returns:
22     a_next -- next hidden state, of shape (n_a, m)
23     c_next -- next memory state, of shape (n_a, m)
24     yt_pred -- prediction at timestep "t", numpy array of shape (n_y, m)
25     cache -- tuple of values needed for the backward pass, contains (a_next, c_next, a_prev, c_prev, xt, parameters)
26     
27     Note: ft/it/ot stand for the forget/update/output gates, cct stands for the candidate value (c tilde),
28           c stands for the memory value
29     """
30     # Retrieve parameters from "parameters"
31     Wf = parameters["Wf"]
32     bf = parameters["bf"]
33     Wi = parameters["Wi"]
34     bi = parameters["bi"]
35     Wc = parameters["Wc"]
36     bc = parameters["bc"]
37     Wo = parameters["Wo"]
38     bo = parameters["bo"]
39     Wy = parameters["Wy"]
40     by = parameters["by"]
41     
42     # Retrieve dimensions from shapes of xt and Wy
43     n_x, m = xt.shape
44     n_y, n_a = Wy.shape
45 
46     ### START CODE HERE ###
47     # Concatenate a_prev and xt (≈3 lines)
48     contact=np.zeros((n_a+n_x,m))
49     contact[:n_a,:] = a_prev
50     contact[n_a:,:] = xt
51     
52     # Compute values for ft, it, cct, c_next, ot, a_next using the formulas given figure (4) (≈6 lines)
53     ft = sigmoid(np.dot(Wf, contact) + bf)                           
54     it = sigmoid(np.dot(Wi,contact) + bi)
55     cct = np.tanh(np.dot(Wc,contact) + bc)
56     c_next = it * cct + ft * c_prev
57     ot = sigmoid(np.dot(Wo,contact) + bo)
58     a_next = ot * np.tanh(c_next)    
59     
60     # Compute prediction of the LSTM cell (≈1 line)
61     yt_pred = softmax(np.dot(Wy, a_next) + by)
62     ### END CODE HERE ###
63                         
64     # store values needed for backward propagation in cache
65     cache = (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters)
66     return a_next, c_next, yt_pred, cache

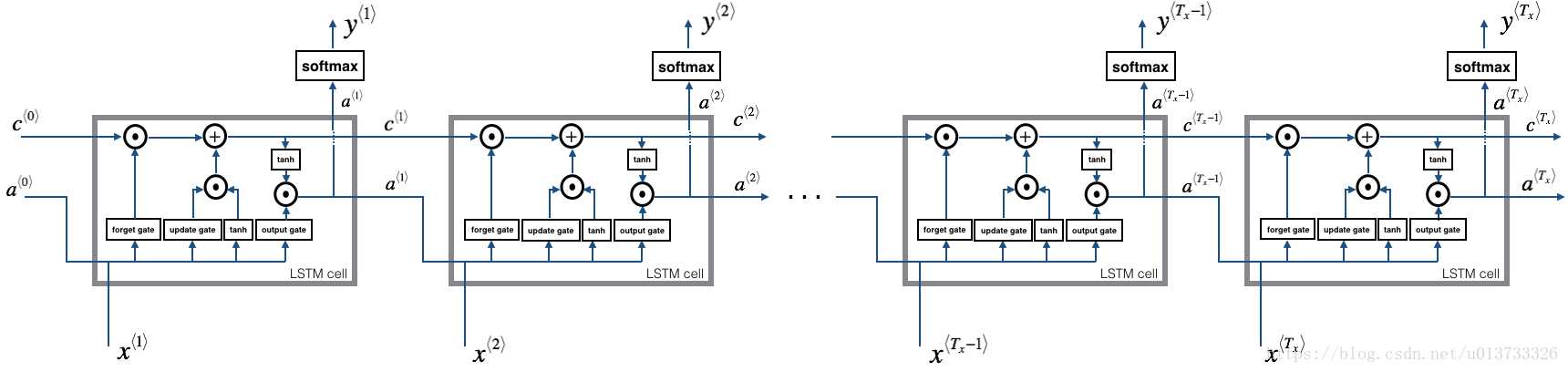
 1 def lstm_forward(x, a0, parameters):
 2     """
 3     Implement the forward propagation of the recurrent neural network using an LSTM-cell described in Figure (3).
 4 
 5     Arguments:
 6     x -- Input data for every time-step, of shape (n_x, m, T_x).
 7     a0 -- Initial hidden state, of shape (n_a, m)
 8     parameters -- python dictionary containing:
 9                         Wf -- Weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
10                         bf -- Bias of the forget gate, numpy array of shape (n_a, 1)
11                         Wi -- Weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)
12                         bi -- Bias of the update gate, numpy array of shape (n_a, 1)
13                         Wc -- Weight matrix of the first "tanh", numpy array of shape (n_a, n_a + n_x)
14                         bc -- Bias of the first "tanh", numpy array of shape (n_a, 1)
15                         Wo -- Weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x)
16                         bo -- Bias of the output gate, numpy array of shape (n_a, 1)
17                         Wy -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
18                         by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
19                         
20     Returns:
21     a -- Hidden states for every time-step, numpy array of shape (n_a, m, T_x)
22     y -- Predictions for every time-step, numpy array of shape (n_y, m, T_x)
23     caches -- tuple of values needed for the backward pass, contains (list of all the caches, x)
24     """
25     # Initialize "caches", which will track the list of all the caches
26     caches = []
27     
28     ### START CODE HERE ###
29     # Retrieve dimensions from shapes of x and Wy (≈2 lines)
30     n_x,m,T_x = x.shape
31     n_y,n_a = parameters[‘Wy‘].shape
32     
33     # initialize "a", "c" and "y" with zeros (≈3 lines)
34     a = np.zeros((n_a, m, T_x))
35     c = np.zeros((n_a, m, T_x))
36     y = np.zeros((n_y, m, T_x))
37     
38     # Initialize a_next and c_next (≈2 lines)
39     a_next = a0
40     c_next = np.zeros((n_a, m))
41     
42     # loop over all time-steps
43     for t in range(T_x):
44         # Update next hidden state, next memory state, compute the prediction, get the cache (≈1 line)
45         a_next, c_next, yt_pred, cache = lstm_cell_forward(x[:,:,t], a_next, c_next, parameters)
46         # Save the value of the new "next" hidden state in a (≈1 line)
47         a[:,:,t] = a_next
48         # Save the value of the prediction in y (≈1 line)
49         y[:,:,t] = yt_pred
50         # Save the value of the next cell state (≈1 line)
51         c[:,:,t] = c_next
52         # Append the cache into caches (≈1 line)
53         caches.append(cache)
54     ### END CODE HERE ###
55     
56     # store values needed for backward propagation in cache
57     caches = (caches, x)
58     return a, y, c, caches

 1 def rnn_cell_backward(da_next, cache):
 2     """
 3     Implements the backward pass for the RNN-cell (single time-step).
 4 
 5     Arguments:
 6     da_next -- Gradient of loss with respect to next hidden state
 7     cache -- python dictionary containing useful values (output of rnn_cell_forward())
 8 
 9     Returns:
10     gradients -- python dictionary containing:
11                         dx -- Gradients of input data, of shape (n_x, m)
12                         da_prev -- Gradients of previous hidden state, of shape (n_a, m)
13                         dWax -- Gradients of input-to-hidden weights, of shape (n_a, n_x)
14                         dWaa -- Gradients of hidden-to-hidden weights, of shape (n_a, n_a)
15                         dba -- Gradients of bias vector, of shape (n_a, 1)
16     """
17     # Retrieve values from cache
18     (a_next, a_prev, xt, parameters) = cache
19     
20     # Retrieve values from parameters
21     Wax = parameters["Wax"]
22     Waa = parameters["Waa"]
23     Wya = parameters["Wya"]
24     ba = parameters["ba"]
25     by = parameters["by"]
26 
27     ### START CODE HERE ###
28     # compute the gradient of tanh with respect to a_next (≈1 line)
29     dtanh = (1 - np.square(a_next)) * da_next
30     
31     # compute the gradient of the loss with respect to Wax (≈2 lines)
32     dxt = np.dot(Wax.T, dtanh)
33     dWax= np.dot(dtanh, xt.T)
34 
35     # compute the gradient with respect to Waa (≈2 lines)
36     da_prev = np.dot(Waa.T, dtanh)
37     dWaa = np.dot(dtanh, a_prev.T)
38 
39     # compute the gradient with respect to b (≈1 line)
40     dba = np.sum(dtanh, keepdims=True, axis=-1)
41     ### END CODE HERE ###
42     
43     # Store the gradients in a python dictionary
44     gradients = {"dxt": dxt, "da_prev": da_prev, "dWax": dWax, "dWaa": dWaa, "dba": dba}    
45     return gradients

 1 def rnn_backward(da, caches):
 2     """
 3     Implement the backward pass for a RNN over an entire sequence of input data.
 4 
 5     Arguments:
 6     da -- Upstream gradients of all hidden states, of shape (n_a, m, T_x)
 7     caches -- tuple containing information from the forward pass (rnn_forward)
 8     
 9     Returns:
10     gradients -- python dictionary containing:
11                         dx -- Gradient w.r.t. the input data, numpy-array of shape (n_x, m, T_x)
12                         da0 -- Gradient w.r.t the initial hidden state, numpy-array of shape (n_a, m)
13                         dWax -- Gradient w.r.t the input‘s weight matrix, numpy-array of shape (n_a, n_x)
14                         dWaa -- Gradient w.r.t the hidden state‘s weight matrix, numpy-arrayof shape (n_a, n_a)
15                         dba -- Gradient w.r.t the bias, of shape (n_a, 1)
16     """     
17     ### START CODE HERE ###
18     # Retrieve values from the first cache (t=1) of caches (≈2 lines)
19     caches, x = caches
20     a1, a0, x1, parameters = caches[0]    
21    
22     # Retrieve dimensions from da‘s and x1‘s shapes (≈2 lines)
23     n_a, m, T_x = da.shape
24     n_x, m = x1.shape
25     
26     # initialize the gradients with the right sizes (≈6 lines)
27     dx = np.zeros([n_x, m, T_x])
28     da0 = np.zeros([n_a, m])
29     dWax = np.zeros([n_a, n_x])
30     dWaa = np.zeros([n_a, n_a])
31     dba = np.zeros([n_a, 1])
32     da_prevt = np.zeros([n_a, m])    
33     
34     # Loop through all the time steps
35     for t in reversed(range(T_x)):
36         # Compute gradients at time step t. Choose wisely the "da_next" and the "cache" to use in the backward propagation step. (≈1 line)
37         gradients = rnn_cell_backward(da[:,:,t] + da_prevt, caches[t])
38         # Retrieve derivatives from gradients (≈ 1 line)
39         dxt, da_prevt, dWaxt, dWaat, dbat = gradients["dxt"], gradients["da_prev"], gradients["dWax"], gradients["dWaa"], gradients["dba"]
40         # Increment global derivatives w.r.t parameters by adding their derivative at time-step t (≈4 lines)
41         dx[:, :, t] = dxt
42         dWax += dWaxt
43         dWaa += dWaat
44         dba += dbat     
45         
46     # Set da0 to the gradient of a which has been backpropagated through all time-steps (≈1 line) 
47     da0 = da_prevt
48     ### END CODE HERE ###
49 
50     # Store the gradients in a python dictionary
51     gradients = {"dx": dx, "da0": da0, "dWax": dWax, "dWaa": dWaa,"dba": dba}    
52     return gradients

 1 def lstm_cell_backward(da_next, dc_next, cache):
 2     """
 3     Implement the backward pass for the LSTM-cell (single time-step).
 4 
 5     Arguments:
 6     da_next -- Gradients of next hidden state, of shape (n_a, m)
 7     dc_next -- Gradients of next cell state, of shape (n_a, m)
 8     cache -- cache storing information from the forward pass
 9 
10     Returns:
11     gradients -- python dictionary containing:
12                         dxt -- Gradient of input data at time-step t, of shape (n_x, m)
13                         da_prev -- Gradient w.r.t. the previous hidden state, numpy array of shape (n_a, m)
14                         dc_prev -- Gradient w.r.t. the previous memory state, of shape (n_a, m, T_x)
15                         dWf -- Gradient w.r.t. the weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
16                         dWi -- Gradient w.r.t. the weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)
17                         dWc -- Gradient w.r.t. the weight matrix of the memory gate, numpy array of shape (n_a, n_a + n_x)
18                         dWo -- Gradient w.r.t. the weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x)
19                         dbf -- Gradient w.r.t. biases of the forget gate, of shape (n_a, 1)
20                         dbi -- Gradient w.r.t. biases of the update gate, of shape (n_a, 1)
21                         dbc -- Gradient w.r.t. biases of the memory gate, of shape (n_a, 1)
22                         dbo -- Gradient w.r.t. biases of the output gate, of shape (n_a, 1)
23     """
24     # Retrieve information from "cache"
25     (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters) = cache
26     
27     ### START CODE HERE ###
28     # Retrieve dimensions from xt‘s and a_next‘s shape (≈2 lines)
29     n_x,m = xt.shape
30     n_a, m = a_next.shape
31     
32     # Compute gates related derivatives, you can find their values can be found by looking carefully at equations (7) to (10) (≈4 lines)
33     dot = da_next * np.tanh(c_next) * ot * (1-ot)
34     dcct = (dc_next * it + ot * (1 - np.square(np.tanh(c_next))) * it * da_next) * (1 - np.square(cct))
35     dit = (dc_next * cct + ot * (1 - np.square(np.tanh(c_next))) * cct * da_next) * it * (1 - it)
36     dft = (dc_next * c_prev + ot * (1 - np.square(np.tanh(c_next))) * c_prev * da_next) * ft * (1 - ft)
37 
38     # Compute parameters related derivatives. Use equations (11)-(14) (≈8 lines)
39     concat = np.concatenate((a_prev, xt), axis=0).T
40     dWf = np.dot(dft, concat)
41     dWi = np.dot(dit, concat)
42     dWc = np.dot(dcct, concat)
43     dWo = np.dot(dot, concat)
44     dbf = np.sum(dft, axis=1, keepdims=True)
45     dbi = np.sum(dit, axis=1, keepdims=True)
46     dbc = np.sum(dcct, axis=1, keepdims=True)
47     dbo = np.sum(dot, axis=1, keepdims=True)
48     
49     # Compute derivatives w.r.t previous hidden state, previous memory state and input. Use equations (15)-(17). (≈3 lines)
50     da_prev = np.dot(parameters[‘Wf‘][:,:n_a].T, dft) +  np.dot(parameters["Wi"][:, :n_a].T, dit) + np.dot(parameters[‘Wc‘][:,:n_a].T, dcct) + np.dot(parameters[‘Wo‘][:,:n_a].T, dot)
51     dc_prev = dc_next * ft + ot * (1-np.square(np.tanh(c_next))) * ft * da_next
52     dxt = np.dot(parameters[‘Wf‘][:, n_a:].T, dft) + np.dot(parameters["Wi"][:, n_a:].T, dit)+ np.dot(parameters[‘Wc‘][:,n_a:].T,dcct) + np.dot(parameters[‘Wo‘][:,n_a:].T, dot)
53     ### END CODE HERE ###
54     
55     # Save gradients in dictionary
56     gradients = {"dxt": dxt, "da_prev": da_prev, "dc_prev": dc_prev, "dWf": dWf,"dbf": dbf, "dWi": dWi,"dbi": dbi,
57                 "dWc": dWc,"dbc": dbc, "dWo": dWo,"dbo": dbo}
58     return gradients

 1 def lstm_backward(da, caches):
 2     """
 3     Implement the backward pass for the RNN with LSTM-cell (over a whole sequence).
 4 
 5     Arguments:
 6     da -- Gradients w.r.t the hidden states, numpy-array of shape (n_a, m, T_x)
 7     dc -- Gradients w.r.t the memory states, numpy-array of shape (n_a, m, T_x)
 8     caches -- cache storing information from the forward pass (lstm_forward)
 9 
10     Returns:
11     gradients -- python dictionary containing:
12                         dx -- Gradient of inputs, of shape (n_x, m, T_x)
13                         da0 -- Gradient w.r.t. the previous hidden state, numpy array of shape (n_a, m)
14                         dWf -- Gradient w.r.t. the weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
15                         dWi -- Gradient w.r.t. the weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)
16                         dWc -- Gradient w.r.t. the weight matrix of the memory gate, numpy array of shape (n_a, n_a + n_x)
17                         dWo -- Gradient w.r.t. the weight matrix of the save gate, numpy array of shape (n_a, n_a + n_x)
18                         dbf -- Gradient w.r.t. biases of the forget gate, of shape (n_a, 1)
19                         dbi -- Gradient w.r.t. biases of the update gate, of shape (n_a, 1)
20                         dbc -- Gradient w.r.t. biases of the memory gate, of shape (n_a, 1)
21                         dbo -- Gradient w.r.t. biases of the save gate, of shape (n_a, 1)
22     """
23     # Retrieve values from the first cache (t=1) of caches.
24     (caches, x) = caches
25     (a1, c1, a0, c0, f1, i1, cc1, o1, x1, parameters) = caches[0]
26     
27     ### START CODE HERE ###
28     # Retrieve dimensions from da‘s and x1‘s shapes (≈2 lines)
29     n_a, m, T_x = da.shape
30     n_x, m = x1.shape
31     
32     # initialize the gradients with the right sizes (≈12 lines)
33     dx = np.zeros((n_x, m, T_x))
34     da0 = np.zeros((n_a, m))
35     da_prevt = np.zeros(da0.shape)
36     dc_prevt = np.zeros(da0.shape)
37     dWf = np.zeros((n_a, n_a + n_x))
38     dWi = np.zeros(dWf.shape)
39     dWc = np.zeros(dWf.shape)
40     dWo = np.zeros(dWf.shape)
41     dbf = np.zeros((n_a, 1))
42     dbi = np.zeros(dbf.shape)
43     dbc = np.zeros(dbf.shape)
44     dbo = np.zeros(dbf.shape)
45     
46     # loop back over the whole sequence
47     for t in reversed(range(T_x)):
48         # Compute all gradients using lstm_cell_backward
49         gradients = lstm_cell_backward(da[:, :, t], dc_prevt, caches[t])
50         # Store or add the gradient to the parameters‘ previous step‘s gradient
51         dx[:,:,t] = gradients["dxt"]
52         dWf += gradients["dWf"]
53         dWi += gradients["dWi"]
54         dWc += gradients["dWc"]
55         dWo += gradients["dWo"]
56         dbf += gradients["dbf"]
57         dbi += gradients["dbi"]
58         dbc += gradients["dbc"]
59         dbo += gradients["dbo"]
60     # Set the first activation‘s gradient to the backpropagated gradient da_prev.
61     da0 = gradients["da_prev"]   
62     ### END CODE HERE ###
63 
64     # Store the gradients in a python dictionary
65     gradients = {"dx": dx, "da0": da0, "dWf": dWf,"dbf": dbf, "dWi": dWi,"dbi": dbi,
66                 "dWc": dWc,"dbc": dbc, "dWo": dWo,"dbo": dbo} 
67     return gradients