隐马尔可夫模型(Hidden Markov model, HMM)

标签：条件   sdn   www   html   产生   ansi   最大   算法   hid   

隐马尔可夫模型(Hidden Markov model, HMM)

• 结构最简单的动态贝叶斯网的生成模型
• 著名的有向图模型
• 典型的自然语言中处理标注问题的统计机器学模型

隐马模型发明者：

鲍姆-韦尔奇（美）(Baum-Welch算法)

隐马模型的三个基本问题：

（1）概率计算问题：前向-后向算法—>动态规划

给定模型λ=（A,B,π）和观测序列O={o1,02,…or},计算模型λ下观测序列O出现的概率P(O|λ)

（2）学习问题：Baum-Welch算法（状态未知）—>EM

已知观测序列O={o1,02,…or},估计模型λ=（A,B,π）的参数，使得在该模型下观测序列P(O|λ)最大

（3）预测问题：Viterbi算法—>动态规划

解码问题：已知模型λ=（A,B,π）和观测序列O={o1,02,…or}，求给定观测序列条件概率P（I|O,λ）最大的状态序列I。

REF：

https://www.cnblogs.com/skyme/p/4651331.html 骰子举例，讲的挺好
假设三个不同的骰子。

• 第一个骰子是我们平常见的骰子（称这个骰子为D6），6个面，每个面（1，2，3，4，5，6）出现的概率是1/6。
• 第二个骰子是个四面体（称这个骰子为D4），每个面（1，2，3，4）出现的概率是1/4。
• 第三个骰子有八个面（称这个骰子为D8），每个面（1，2，3，4，5，6，7，8）出现的概率是1/8。
  

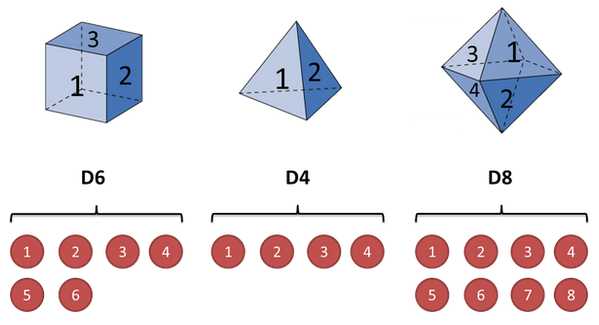
开始掷骰子，先从三个骰子里挑一个，挑到每一个骰子的概率都是1/3。
继续掷骰子，得到一个数字，1，2，3，4，5，6，7，8中的一个。
不停的重复上述过程，我们会得到一串数字，每个数字都是1，2，3，4，5，6，7，8中的一个。
可能得到这么一串数字（掷骰子10次）：1 6 3 5 2 7 3 5 2 4 ，这串数字叫做可见状态链。
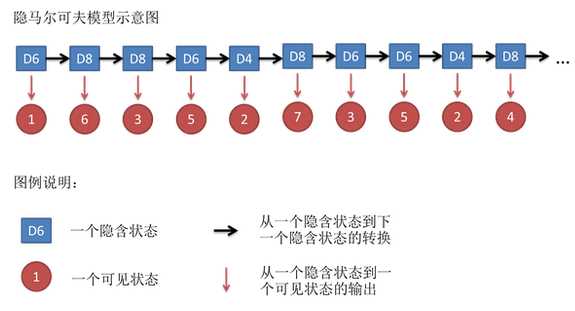
但是在隐马尔可夫模型中，不仅仅有这么一串可见状态链，还有一串隐含状态链。
在这个例子里，这串隐含状态链就是你用的骰子的序列。比如，隐含状态链有可能是：D6 D8 D8 D6 D4 D8 D6 D6 D4 D8 。

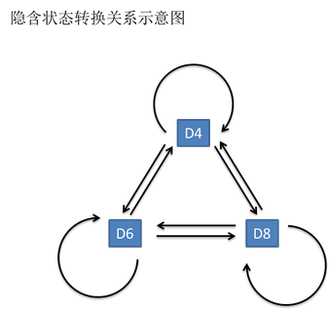
一般来说，HMM中说到的马尔可夫链其实是指隐含状态链，因为隐含状态（骰子）之间存在转换概率（transition probability）。
在我们这个例子里，D6的下一个状态是D4，D6，D8的概率都是1/3。D4，D8的下一个状态是D4，D6，D8的转换概率也都一样是1/3。
这样设定是为了最开始容易说清楚，但是我们其实是可以随意设定转换概率的。
比如，我们可以这样定义，D6后面不能接D4，D6后面是D6的概率是0.9，是D8的概率是0.1。
这样就是一个新的HMM。

同样的，尽管可见状态之间没有转换概率，但是隐含状态和可见状态之间有一个概率叫做输出概率（emission probability）。
就我们的例子来说，六面骰（D6）产生1的输出概率是1/6。产生2，3，4，5，6的概率也都是1/6。
我们同样可以对输出概率进行其他定义。比如，我有一个被赌场动过手脚的六面骰子，掷出来是1的概率更大，是1/2，掷出来是2，3，4，5，6的概率是1/10。

https://blog.csdn.net/z2536083458/article/details/99696875 较为经典的讲解
https://www.jianshu.com/p/ca483c79182e

隐马尔可夫模型(Hidden Markov model, HMM)

标签：条件   sdn   www   html   产生   ansi   最大   算法   hid   

原文地址：https://www.cnblogs.com/hbuwyg/p/13231306.html