标签：有助于 更换 完美解决 effect 问题： 例子 理想 记录 code
这篇cvpr2019的论文主要提出了一个损失函数Class-Balanced Loss用来处理数据长尾问题
长尾问题是由于分类问题中数据集每类的数据量不同，导致分类准确度下降。举个极端点的例子有助于理解：A、B二分类问题，数据集中，A、B数据量比例为999：1，为了减少损失值，网络很自然的将所有图片都分到A类，这样准确率为99.9%，但是明显这个网络不能用。
为了解决长尾问题，前人也提出了不少办法，比如将B图片数据增强，缩放、旋转、平移、裁剪，使得B类别中有999张图片，这样数据就均衡了；或者给A的损失值之前加一个权重系数（1/999）。理想很丰满，现实很骨感。这样做提升效果有限。
为什么呢？打个比方：假设AB两个类别分别是一个圆形，数据集中的数据就是圆形中的点。如果训练时你能把圆中每个点都取到了，测试时网络的准确率一定是100%，毕竟所有点都记录在案了。然而实际上不可能取到圆中每一个点，同样也不能取到类中的每一个数据。我们可以退而求其次，如果能从圆中均匀的取足够多的点，也能反应出这个圆（类别）的特性。然而用上面提到的两种方法做数据增强，相当于在已有点周围取点，很明显这些点不能反映圆（类别）的特性。
那什么样的点能够反映圆的特性呢？换言之，哪些点是有效的，哪些点是无效的呢？
这篇论文一开始就提出一个概念：Effective Number（有效数据，用E来表示），如果知道了每个类别中的有效数据数量，问题似乎就好办多了：CB = 1/E * L 。其中CB是本文提出的Class-Balanced Loss，L是普通损失函数，可以任意更换。
现在要做的就是求有效数据E。先给结论：
，其中
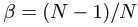，N为有效样本的上限，该类别的采样数（数据集中该类别的图片数量），可以用归纳法证明
当n=1时，E1=1
当n>1时，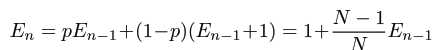
，因为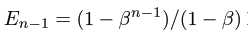
所以，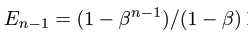
所以最终，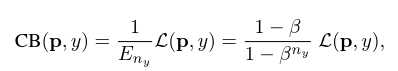
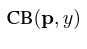是Class-Balanced Loss
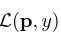是普通损失函数，可以任意更换。
由于现实中，N无法得到，因此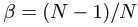无法计算，因为N几近无穷，因此β取一个接近1的数，作者代码里给的是0.9999。
这样，这个问题就完美解决。
作者在论文里还尝试了该算法与一些传统算法结合，效果也不错：
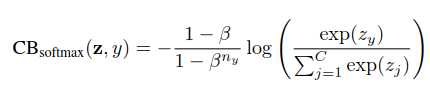
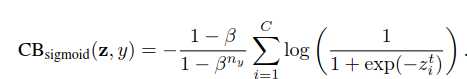
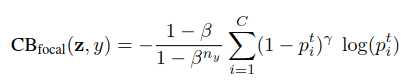
处理长尾问题：Class-Balanced Loss Based on Effective Number of Samples
标签：有助于 更换 完美解决 effect 问题： 例子 理想 记录 code
原文地址：https://www.cnblogs.com/jiangnanyanyuchen/p/13232195.html
