图论 最短路总结

标签：中转   lag   时间复杂度   调试   com   入队   最短路算法   不能   bellman   

写在前面：图论题的调试真感人
让我们进入正题

最短路是啥

emmm 顾名思义最短路就是求一个点到另外一个点的最小距离
一般来说最短路分为：单源最短路和多源最短路
单源最短路就是求一个源点到另外多个点的最短距离
而多源最短路就是求多个点到其他点的最短距离
算法一般有：

• floyd（多源 O(\(n^3\))）
• dijkstra（单源 O(\(n^2\)) 可用堆优化到O(\(n*log_n\))）
• Bellman-Ford(单源 O(\(nE\)))
• SPFA(单源 O(nE 但是比BF强))
  具体的优劣以及使用范围我们会在下面具体讲解

floyd 算法

• 适用范围 ： 多源最短路 可处理负权 但是不能处理负环 运行一次可求得任意两点间最短路
• floyd算法其实很好理解 也很好写（毕竟 O(\(n^3\))）有的时候可以将其当作dp理解
• 先来想这样一个问题 ：
  现在你在老家（B地）自由自在的玩耍着 突然有人告诉你去A地能给你分对象 （咳咳） 然后你就屁颠屁颠的跑去了A地 但是有好多人都要去A地 你希望可以最快到达A地（也就是路径最短）
• 显然你可以直接坐车从B地直接赶往A地 但是这样一定是最短的吗？
  然并卵 毕竟路上你要走山路十八弯 而这时C地出现在你的面前 从B直接到A要走1000km（反正很远很远） 但是从B到C只需要 1 km，从C到B呢也只需要 1 km（反正很短很短）那你肯定会先到C 再到B吧
• 这就是我们的核心思路了
  揪黑板！！
  如果我们已知并记录了从i到j的最短路径 而如果将k作为中转点可以使得我们的最短路径更短 那我们就更新i到j的最短路径 （其他算法也会用到这个思想，即下面的松弛操作）

核心代码实现：

for(int k=1;k<=n;++k)//枚举中转点
    for(int i=1;i<=n;++i)//枚举边的起点
        for(int j=1;j<=n;++j)//枚举边的终点
            if(a[i][j]>a[i][k]+a[k][j])//松弛操作（即利用第三个点来判断是否可以更新目标两个点的最短距离）
                a[i][j]=a[i][k]+a[k][j];//a[i][j]是从i到j的最小值

关于k为什么要枚举在第一层循环:
刚才已经说过floyd类似于dp，而k就是dp的阶段（dp的阶段显然要枚举在第一层的），其实a本来是三维a[k][i][j]表示只经过前k个点从i到j的最短路，而可以将第一维的k舍去（like背包） 所以就成了现在的样子啦

dijkstra 算法

• 适用范围：单源最短路 不能处理带有负权边的图 需要指定起点s
• dij是求最短楼最常用的方法也是最经典的：
  然后维护一个集合S用于存放已经知道对于源点s的最短距离的点
  另外一个集合U用于维护还不知道对于源点s的最短距离的点（但是可以知道当前不完全状态下的最短距离）
• 初始时 S中只有s自己 距离自己的距离是0 而其他点距离s的距离都初始化为正无穷
  然后我们利用这个点来求出对于其他点的最短距离

1. 首先进行一次松弛操作 将s可以直接到达的点的距离dis[i]记录下来 然后更新i点的距离（如果比当前已知的s到i的最短距离更短的话）
2. 从U集合中选出一个距离s最短的点 将其加入到S集合中 然后利用这个点再去更新另外一些点的距离
3. 在新出现的点中选出距离s最短的点 加入到S集合中 然后再利用新点再去更新其他点距离
4. 重复以上步骤知道目标点距离源点s的距离求出或者无法再更新

• 下面是图例演示
  

核心代码实现 ：

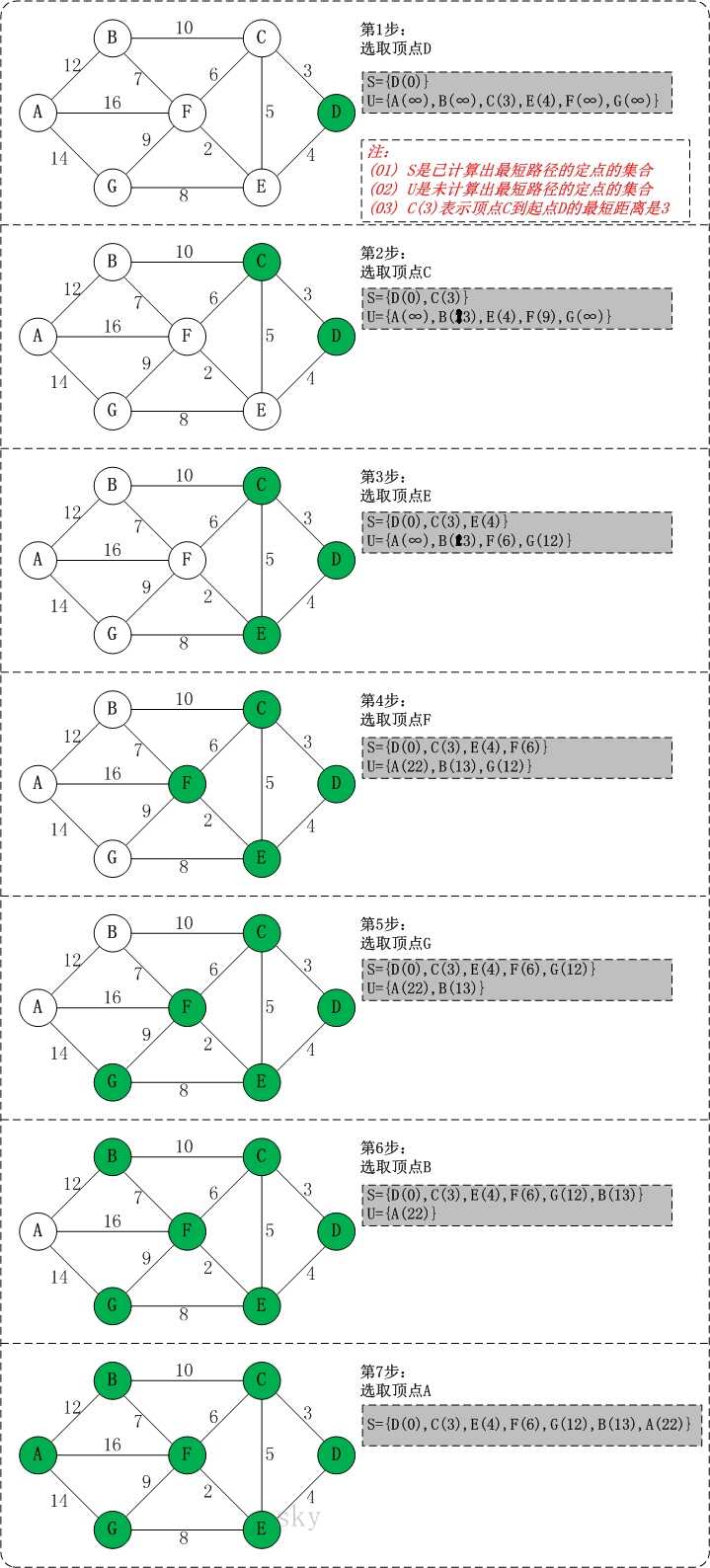
void dij(int s){
	memset(vis,0,sizeof(vis));
	vis[s] = 1;//将s放入S集合
	for(int i = 1;i <= n;++i){
		if(g[s][i]){dis[i] = g[s][i];}//如果从s到i有路的话 就将s到i的距离设置为长度
		else dis[i] = 0x3f3f3f3f;//将其他点设置为正无穷（即目前无法到达）
	}
	dis[s] = 0;//源点s到自己的最短距离是0
	for(int i = 1;i < n;++i){//遍历每一个点以求出每一个点距离源点的最小距离
		int Min = 0x3f3f3f3f,k = 0;//Min维护这一轮维护后要放入S集合的距离最小值，k维护要放入S集合的点
		for(int j = 1;j <= n;++j)
			if(!vis[j] && Min > dis[j]){//如果点j还没有在S集合中并且s到当前节点的距离更小
				Min = dis[j];k = j;
			}
		vis[k] = 1;//k放入S集合
		for(int j = 1;j <= n;++j){
			if(g[k][j] && dis[j] > dis[k] + g[k][j]){//如果可以通过k松弛
				dis[j] = dis[k] + g[k][j];//更新到j的最小值
			}
		}
	}
}

关于优化：

• 上一个只是朴素的最短路算法 有的时候并不能满足我们的要求（和出题人丧心病狂的卡空间时间）
• 我们可以用邻接表去存边 后面遍历的时候就可以用邻接表了 这样的时间复杂度大约是常数 远低于朴素算法的O(n)
• 求集合外的点到源点的最小值我们可以建一个小根堆，这样我们的时间复杂度就是进堆的时间消耗 ， 为O\((Elog_E\)),（E为边数），这里用优先队列进行操作

核心代码实现：

void dij(int x){
	priority_queue<node> q;
	memset(vis,0,sizeof(vis));
	memset(dis,0x3f,sizeof(dis));
	dis[x] = 0;
	q.push(node(x,0));
	while(!q.empty()){
		node t = q.top();q.pop();
		int k = t.num;
		if(vis[k])continue;
		vis[k] = 1;
		for(int i = head[k];i;i = a[i].next){
			int v = a[i].to;
			if(dis[v] > dis[k] + a[i].dis){
				dis[v] = dis[k] + a[i].dis;q.push(node(v,dis[k] + a[i].dis));
			}
		}
	}
}

Bellman-ford算法

• 适用范围 : 基本啥也能用 （前提是不考虑时间复杂度情况下）
• 算法思想：和dij很像 但是这里是沿着边进行松弛操作
• 对于有向带权图， 从源点s开始，利用Bellman-ford，依次求解各顶点的最短距离，
  算法概况：

for(int i = 0;i < n;++i)//枚举顶点
      for each(i,j)//对于每一条边
            song_chi(i,j)//松弛操作

• BF算法对每一条边做松弛操作 ， 并且重复了n次，因此算法的时间复杂度为O(n*E)

核心代码实现：

void BF(int u){
	memset(d,0x3f,sizeof(d));
	d[u] = 0;
	for(int i = 1;i < n;++i){
		for(int j = 1;j <= cnt;++j){//cnt存的是图中共有几个边
			int x = a[j].from,y = a[j].to,z = a[j].dis;
			d[y] = min(d[y],d[x] + z);//松弛操作
		}
	}
}

• 买一送一 BF算法更加实惠 当当当当当
  咳咳 既然dij和BF感觉实现方法差不多 但是BF有一个dij不能企及的地方：判负环
  如果我们通过BF算法求得了各个点到源点s的最短路 然后再进行一次松弛呢？
  如果有负环的话是不是我们会再重新跑一遍负环然后让各个点的值更小？ 所以利用这个性质我们就可以来判断是否有负环啦！

bool check(){
	for(int i = 1;i <= cnt;++i){
		int x = a[i].from,y = a[i].to,z = a[i].dis;
		if(d[y] < d[x] + z)return 1;
	}
	return 0;
}
//主函数中：
if(check()){
	printf("NO\n");return 0;
}

SPFA算法

• 适用范围：反正BF能用的它都能用（文章开头说过它可以看成是BF的优化）
• BF每次都通过所有的边来松弛出一个新点的最短距离 但是这样太浪费了
• 只有那些已经松弛过的点才可能去松弛别的点，所以我们可以用一个队列来记录松弛成功了的点，以此用这些点来松弛邻接点（显然优化不小吧 能写这个就写这个 嘿嘿 如果你刚刚看过BF并且苦思冥想请不要怪罪博主 还能提高代码能力的）

核心代码实现

struct node{
	int to,dis,next;
}a[maxn];

void add(int x,int y,int z){
	a[++cnt].to = y;a[cnt].next = head[x];a[cnt].dis = z;head[x] = cnt;
}

bool spfa(int s){
	memset(dis,0x3f,sizeof(dis));dis[s] = 0;//dis存到源点的最短距离
	queue<int>q;
	q.push(s);flag[s] = 1;//s入队
	while(!q.empty()){
		int u = q.front();q.pop();flag[u] = 0;//因为一个节点u可能多次进队
		for(int i = head[u];i;i = a[i].next){//邻接表存边
			int v = a[i].to;
			if(dis[v] > dis[u] + a[i].dis){//松弛操作：没错，还是我！！！
				dis[v] = dis[u] + a[i].dis;
				if(!flag[v]){//优化
					if(++num[v] >= n)return 0;如果同一个点被多次松弛 那么肯定有负环（这个判断也比刚才的少女口阿  把前辈666扣在公屏上）
					q.push(v);flag[v] = 1;//v进队，标记
				}
			}
		}
	}
	return 1;
}
//主函数中：
if(!spfa(源点))输出NO
else 输出距离

好了 本文阅读到此结束了

码字不易 推荐走起

如果您有不懂的地方 或者 您发现代码有问题可以在下方评论或者给博主留言

感谢观看>_<

图论 最短路总结

标签：中转   lag   时间复杂度   调试   com   入队   最短路算法   不能   bellman   

原文地址：https://www.cnblogs.com/2004-08-20/p/13232330.html