[ML L4] Decision Tress

标签：fir   not   eva   org   tin   sci   blank   table   most   

Decision trees can handle none linear speratable dataset, in the picture, there is none separable dataset

When we use dscision tree, we ask multi linear separable questions:

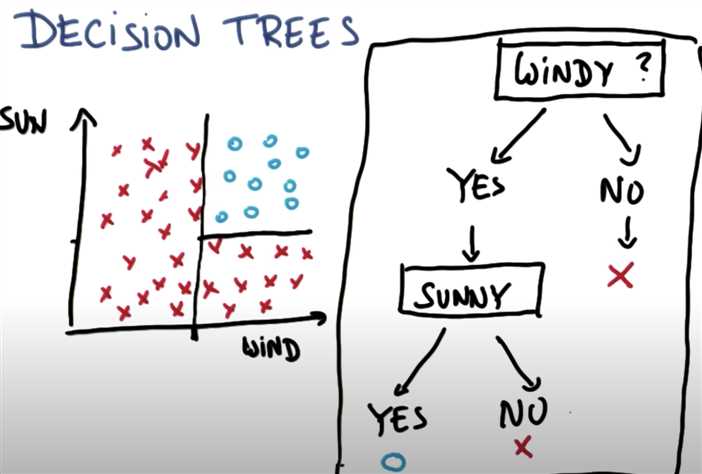
For example, we can ask, 

1. Is windy?

2. Is Sunny?

Then we can reach our correct classified dataset.

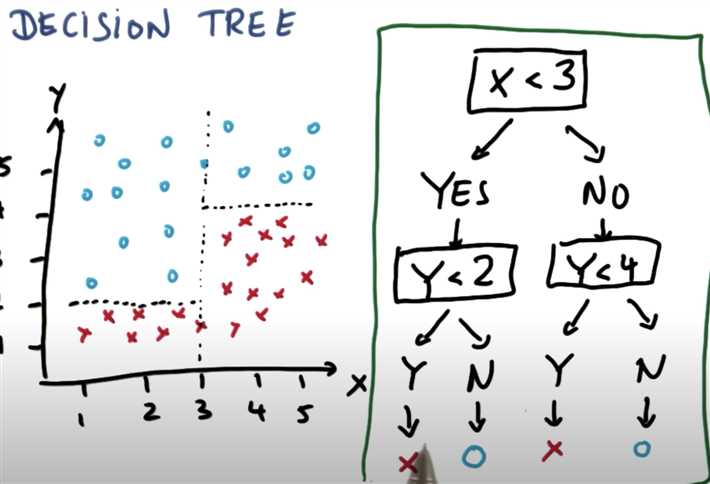
Another Example:

First, on the left hand side: ask ‘x<3‘ then we will got better answer.

Then ask ‘y < 2‘ to separae data.

Second, on the right hand side: 

Code:

>>> from sklearn import tree
>>> X = [[0, 0], [1, 1]]
>>> Y = [0, 1]
>>> clf = tree.DecisionTreeClassifier()
>>> clf = clf.fit(X, Y)

Example of output for DT:

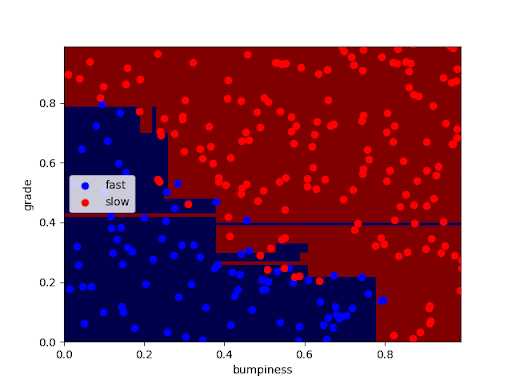
Overfitting:

https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html#sklearn.tree.DecisionTreeClassifier

Sometimes, results migth be overfitting, one params we can modify to solve the problme is ‘min_sample_split‘:

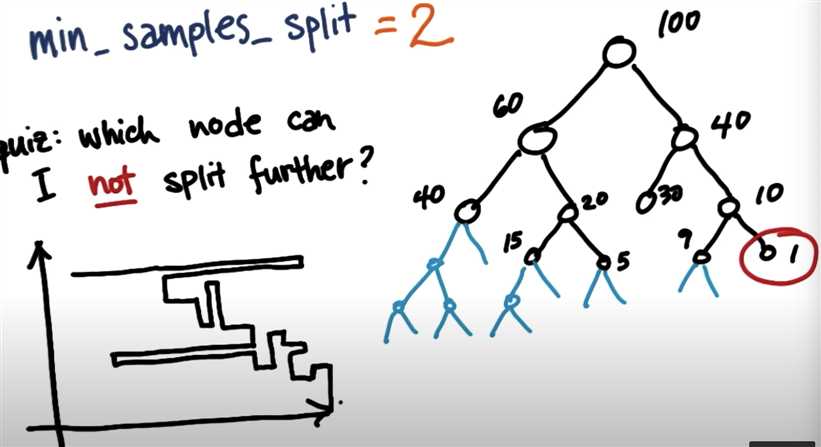
In the picture, right most only contains one dataset, so not able to split further.

Entropy:

Controls how a DT decides where to split the data

definition: measure of impurity in a bunch example:

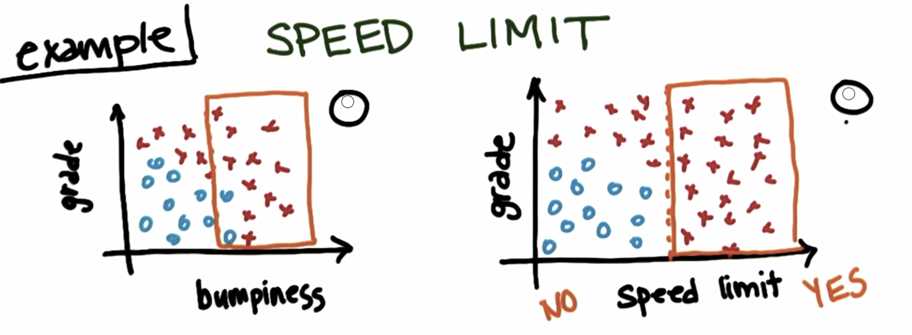
Try to get all dataset classified as correct as possible. In the example, right one is better.

Calculation Entropy:

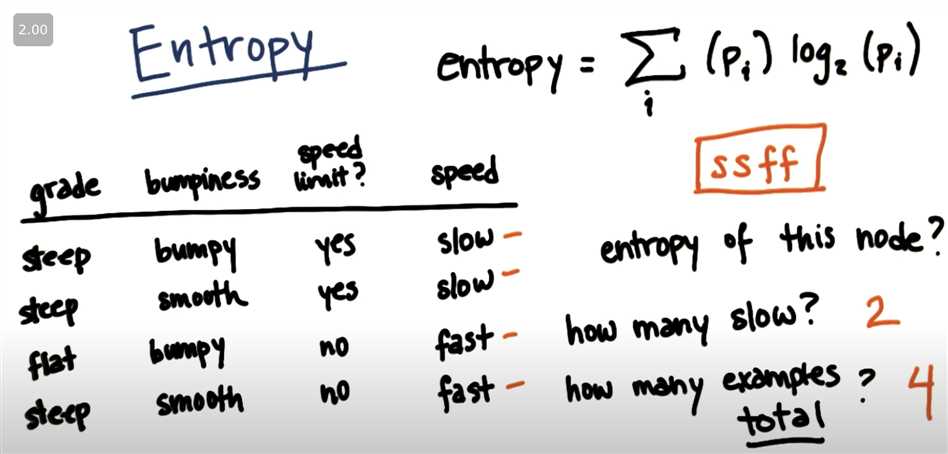
So Pi(slow) should be 2 / 4 = 0.5

Pi(fast) = 1 - 0.5 = 0.5

Entropy:

import math

e = -0.5 * math.log(0.5, 2) - 0.5 * math.log(0.5, 2) // 1

 E(parent) = 1

Information Gain:

Information gain calculates the reduction in entropy or surprise from transforming a dataset in some way.

It is commonly used in the construction of decision trees from a training dataset, by evaluating the information gain for each variable, and selecting the variable that maximizes the information gain, which in turn minimizes the entropy and best splits the dataset into groups for effective classification.

Number is the bigger the better.

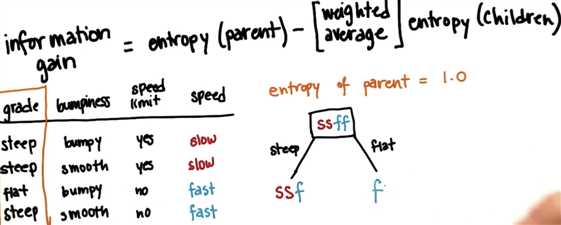
For example, we use ‘grade‘ as chid entropy, as we can see, there are two categories:

• steep
• flat

Based on partent: ‘ssff‘

     for ‘steep: we got 2 slow + 1 fast

     for ‘flat‘: we got 1 fast.

For the Node one the right (F): 

　　entropy for this should be 0. because it only contains one category

For the Node one the left (SSF):

　　P(slow) = 2/3

　　P(fast) = 1/3

　　E(left) = -2/3 * Log(2/3) - 1/3 * Log(1/3) = 0.9184

import math

p_slow = 2 / float(3)
p_fast = 1/float(3)

e = -1 * p_slow * math.log(p_slow, 2) - p_fast * math.log(p_fast ,2)

To calculate entropy(children) = 3/4*0.9184 + 1/4*0 = 0.6889

entropy(parent) = 1

Information Gain = E(parnet) - E(Children) = 1 - 0.6888 = 0.3112

The best separation would be ‘speed limit‘:

[ML L4] Decision Tress

标签：fir   not   eva   org   tin   sci   blank   table   most   

原文地址：https://www.cnblogs.com/Answer1215/p/13222050.html