标签:存储 n+1 基础 param 数字 mamicode 方法 一点 下标
对于一个问题的算法来说,之所以称之为算法,首先它必须能够解决这个问题(称为准确性)。其次,通过这个算法编写的程序要求在任何情况下不能崩溃(称为健壮性)。
如果准确性和健壮性都满足,接下来,就要考虑最重要的一点:通过算法编写的程序,运行的效率怎么样。
运行效率体现在两方面:
好算法的标准就是:在符合算法本身的要求的基础上,使用算法编写的程序运行的时间短,运行过程中占用的内存空间少,就可以称这个算法是“好算法”。
调查表明,人们对于软件或者 APP 的运行效率有极高的要求,例如对于网页打开的忍耐极限是 6 秒甚至更短,如果你设计的网页打开的时间超过 6 秒,多数人会在 4 秒甚至 3 秒的时候毫不犹豫地关掉而去浏览其他网页。在这个大背景下,一个好的“算法”更注重的是时间复杂度,而空间复杂度只要在一个合理的范围内就可以。
计算一个算法的时间复杂度,不可能把所有的算法都编写出实际的程序出来让计算机跑,这样会做很多无用功,效率太低。实际采用的方法是估算算法的时间复杂度。
之前讲过,程序由三种结构构成:顺序结构、分支结构和循环结构。顺序结构和分支结构中的每段代码只运行一次;循环结构中的代码的运行时间要看循环的次数。
由于是估算算法的时间复杂度,相比而言,循环结构对算法的执行时间影响更大。
所以,
算法的时间复杂度,主要看算法中使用到的循环结构中代码循环的次数(称为“频度”)。次数越少,算法的时间复杂度越低。
例如:(C语言代码)
a) ++x; s=0;
b) for (int i=1; i<=n; i++) { ++x; s+=x; }
c) for (int i=1; i<=n; i++) { for (int j=1; i<=n; j++) { ++x; s+=x; } }
上边这个例子中,a 代码的运行了 1 次,b 代码的运行了 n 次,c 代码运行了 n*n 次。
算法的时间复杂度的表示方式为:
O(频度)
这种表示方式称为大“O”记法。
注意,是大写的字母
O,不是数字0。
对于上边的例子而言,a 的时间复杂度为O(1),b 的时间复杂度为O(n),c 的时间复杂度为为O(n^2)。
如果a、b、c组成一段程序,那么算法的时间复杂度为O(n^2+n+1)。但这么表示是不对的,还需要对n^2+n+1进行简化。
简化的过程总结为3步:
n^2+n+1,直接变为 n^2+n)n^2+n 变成 n^2)1,去掉系数。(n^2 系数为 1)所以,最终a、b和c合并而成的代码的时间复杂度为O(n^2)。
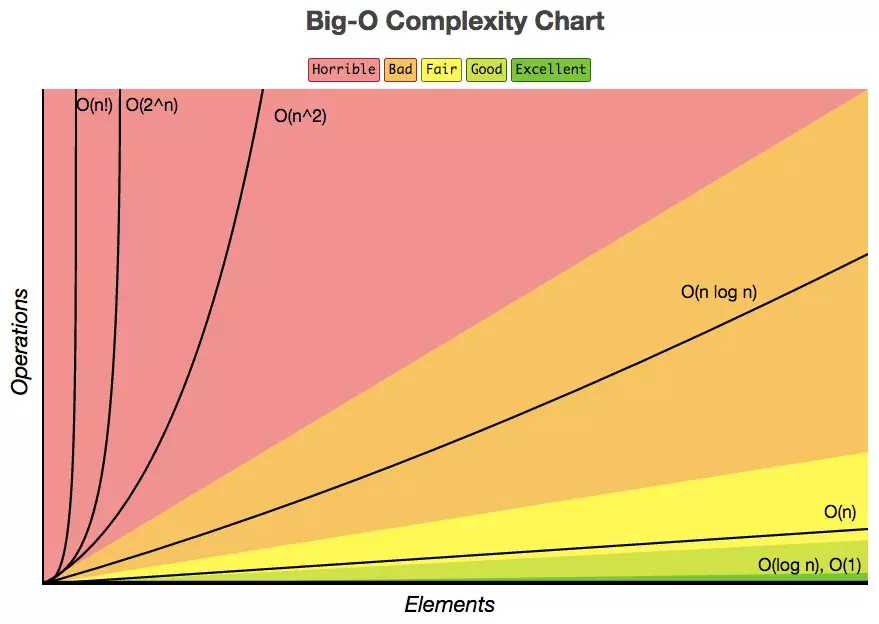
列举了几种常见的算法时间复杂度的比较(又小到大):
O(1)常数阶 < O(logn)对数阶 < O(n)线性阶 < O(n^2)平方阶 < O(n^3)(立方阶) < O(2^n) (指数阶)
算法的时间复杂度和空间复杂度是可以相互转化的。
谷歌浏览器相比于其他的浏览器,运行速度要快。是因为它占用了更多的内存空间,以空间换取了时间。
算法中,例如判断某个年份是否为闰年时,如果想以时间换取空间,算法思路就是:当给定一个年份时,判断该年份是否能被4或者400整除,如果可以,就是闰年。
如果想以空间换时间的话,判断闰年的思路就是:把所有的年份先判断出来,存储在数组中(年份和数组下标对应),如果是闰年,数组值是1,否则是0;当需要判断某年是否为闰年时,直接看对应的数组值是1还是0,不用计算就可以马上知道。
分析算法时,存在几种可能的考虑:
比如:如果要排序一个数组,然后这个数组是已经排序好的数组,那么对这个数组进行排序,速度会非常快。这属于最好情况。
我们主要关注算法的最坏情况,亦即最坏时间复杂度。
def hello():
print(‘hello‘)
这个函数执行了 1 代码。 渐进复杂度:O(1)
def hello1():
print(‘hello‘)
print(‘hello‘)
print(‘hello‘)
这个函数执行的代码次数是 3。复杂度是: O(1)
def hello2():
for _ in range(20):
print(‘hello‘)
这段代码我们就说,这段代码执行了20次语句。
def hello3():
for _ in range(20):
print(‘hello‘)
print(‘hello‘)
print(‘hello‘)
这段代码花费的时间是:60。复杂度是: O(1)
def hello4(n):
for _ in range(n):
print(‘hello‘)
print(‘hello‘)
print(‘hello‘)
这段代码花费的时间是:3n。复杂度是: O(n)
def hello5(n):
for _ in range(n):
print(‘hello‘) # 被执行 n 次
print(‘hello‘) # 被执行 n 次
for _ in range(n):
print(‘hello‘) # 被执行 n * n 次(n的平方)
print(‘hello‘) # 被执行 n * n 次(n的平方)
这段代码花费的时间是:n + n + n^2 + n^2 = 2n + 2n^2 = 2(n^2+n) 。复杂度是:O(n^2)
代码花费的时间主要就是通过代码被执行的次数来判断,有一些复杂的代码是需要很强的数学功底才能算出执行的次数,对于此我们知道常见的即可。
标签:存储 n+1 基础 param 数字 mamicode 方法 一点 下标
原文地址:https://www.cnblogs.com/wy919/p/13234303.html