二进制小数和IEEE浮点标准

标签：博客专栏   details   net   注意   因此   tail   load   --   技术   

二进制小数

首先复习进位计数制的要素：

1. 数码：用来表示进制数的元素。比如

   • 二进制数的数码为：0,1
   • 十进制数的数码为：0,1,2,3,4,5,6,7,8,9
   • 十六进制数的数码为：0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F

2. 基数：数码的个数。比如

   • 二进制数的基数为2
   • 十进制数的基数为10
   • 十六进制数的基数为 16

3. 位权：数制中每一固定位置对应的单位值称为位权。

   • 二进制第2位的位权为\(2^1\)，第3位的位权为\(2^2\)：\((10010.1110)_2 = 1 * 2^4 + 0 * 2^3 + 0 * 2^2 + 1 * 2^1 + 0 * 2^0 + 1 * 2^{-1} + 1 * 2^{-2} + 1 * 2^{-3} + 0 * 2^{-4} = 16 + 2 + 1/2 + 1/4 + 1/8\)
   • 十进制第2位的位权为\(10^1\)，第3位的位权为\(10^2\)：\((123.45)_{10}＝1×10^2+2×10^1+3×10^0+4×10^{-1}+5×10^{-2}\)
   • 十六进制第2位位权为\(16^1\)，第3位的位权为\(16^2\)：\((BAD)_{16} =11× 16^2+10×16^1+13×16^0=(2989)_{10}\)

   总结来说

   • 十进制表示公式为：

     

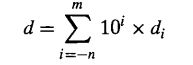
   • 二进制表示公式为：

     

• 注意：二进制小数不像整数一样，只要位数足够，它就可以表示所有整数。假设我们仅考虑有限长度的编码，那么二进制小数无法精确的表示任意小数，比如十进制小数0.2，我们并不能将其准确的表示为一个二进制数，只能增加二进制长度提高表示的精度。如下图所示，二进制表示十进制的0.2只能无限接近，却永远无法精确表示0.2。

IEEE 浮点表示

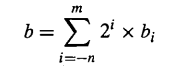
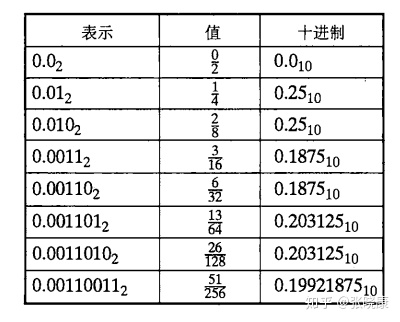
于是为了在计算机中准确表示浮点数，IEEE指定了一条标准来规范表示浮点数，若不对浮点数的表示作出明确的规定，同一个浮点数的表示就不是唯一的。例如\((1.75)_{10}\)可以表示成\(1.11×2^0\)，\(0.111×2^1\)，\(0.0111×2^2\)等多种形式。

IEEE，电气和电子工程师协会( 全称是Institute of Electrical and Electronics Engineers)是一个国际性的电子技术与信息科学工程师的协会，是目前全球最大的非营利性专业技术学会，IEEE 754 标准是IEEE二进位浮点数算术标准（IEEE Standard for Floating-Point Arithmetic）的标准编号。

浮点数的存储格式

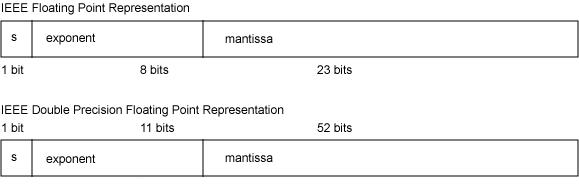
IEEE754 标准中规定：

1. Float 单精度浮点数，用 1 位表示符号，用 8 位表示阶码，用 23 位表示尾数，一共32位。
2. double 双精度浮点数，用 1 位表示符号，用 11 位表示阶码，52 位表示尾数，一共64位。

• 阶码：阶码是整数，阶符和 m 位阶码的数值部分共同反映 浮点数的表示范围及小数点的实际位置 ，常用移码或补码表示。IEEE754标准中采用移码的表示形式。

  • 移码：移码（又叫增码）是对真值补码的符号位取反，一般用作浮点数的阶码，引入的目的是便于浮点数运算时的对阶操作。

  

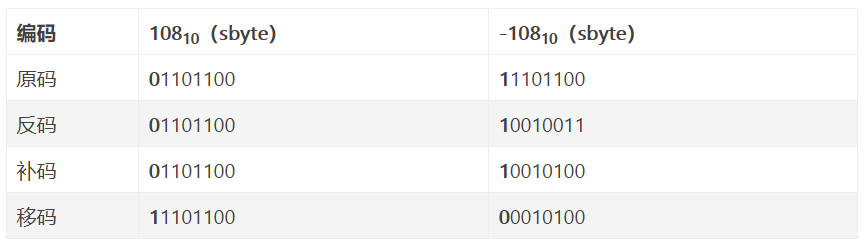
• 尾数：数符表示浮点数的符号，尾数的数值部分的位数 n 反映浮点数的 精度 ，常用原码或补码表示。IEEE754标准中采用原码的表示形式

浮点数的表示格式

浮点数表示法是指以适当的形式将比例因子表示在数据中，让小数点的位置根据需要而浮动。这样，在位数有限的情况下，既扩大了数的表示范围，又保持了数的有效精度。

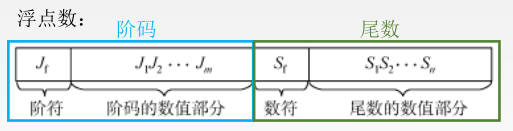
浮点数的真值为：

其中

• S代表符号位，取值为0或1
• e代表指数，E代表阶码
  • \(e=E-127(Float)\)，\(e=E-1023(Double)\)
  • \(E=e_移-1\)
  • 计算指数e时，对阶码E的计算采用原码的计算方式，因此单精度浮点数(Float)的阶码E为8位的取值范围是0到255。根据规定，阶码E既不全为0（数值0），也不全为1。
  • 所以单精度下8位阶码E的规格化的浮点数阶码范围是1至254，因此指数e的范围则为-126至127。
  • 双精度下11位阶码E的规格化的浮点数阶码范围是1至2046，所以指数e范围为-1022至1023。
• M代表尾数，决定浮点数的精度，它是一个二进制小数，表示为\(M=1+f\)
  • 其中\(f\)是n 位的尾数所表示的小数值，满足\(0\le f<1\)，其二进制表示为：\(\small {0.f_{n-1}f_{n-2}\cdot \cdot \cdot f_{1}f_{0}}\) ，也就是二进制小数点在最高有效位的左边。
  • 由于是\(1+f\)，所以我们又可以看成\(\small {1.f_{n-1}f_{n-2}\cdot \cdot \cdot f_{1}f_{0}}\)
  • 所以尾数的范围为\(1 \le M < 2\)

由上面的每个对应位置的范围，我们可以求得

• 单精度最小规格化正数为：\(x=(-1)^0×2^{-126}×1\)
• 单精度最大规格化正数为：\(x=(-1)^0×2^{127}×(2-2^{-23})\)

例题

a：

0,01，其中0代表是正数，所以原码和补码相同，01→\(0*2^1+1*2^0=1\)，所以阶码为+1

1.1001，其中1代表是负数，所以原码为补码末尾减一(1000)，按位取反(0111)，对应真值为-0.0111=\(-(2^{-2}+2^{-3}+2^{-4})=-\frac{7}{16}\)

所以\(a=2^1×(-0.0111)=2^1×(-\frac{7}{16})=-\frac{7}{8}\)

b:

0,01，对应真值为+1

0.01001对应真值为+0.01001=\(+(2^{-2}+2^{-5})=+\frac{9}{32}\)

所以\(b=2^1×(+0.01001)=2^1×\frac{9}{32}=\frac{9}{16}\)

规格化单精度浮点数

为了提高数据的表示精度同时保证数据表示的唯一性，需要对浮点数做规格化处理。

在计算机内，对非0值的浮点数，要求尾数的绝对值必须大于基数R(这里R=2)的倒数，即\(|M|≥1/R\)

0.5规格化

0.5的二进制为0.1

符号位S为0，指数为\(e=-1\)（为啥？我猜是因为0.1中1的最高位是-1），规格化后尾数为1.0（为啥？因为M最小为1.0）。

单精度浮点数尾数域共23位，右侧以0补全，尾数域：

阶码E:

对照单精度浮点数的存储格式，将符号位S，阶码E和尾数域M存放到指定位置，得0.5的机器码：

1.5规格化

1.5的二进制为1.1
符号位为0，指数\(e=0\)（为啥？我猜是因为1.1中1的最高位是0），规格化后尾数为1.1（为啥？因为二进制为1.1，所以M就是1.1，如果二进制是1111，M就是1.111）。

尾数域Ｍ右侧以0补全，得尾数域:

阶码E：

得1.5的机器码：

5规格化

5的二进制为101

符号位为0，指数为\(e=2\)，规格化后尾数为1.01（为啥？因为二进制为101，所以M就是1.01）。

单精度浮点数尾数域共23位，右侧以0补全，尾数域：

阶码E:

得5的机器码：

参考文献

浮点数的表示 -- 基本格式、规格化、表示范围_starter_____的博客-CSDN博客_浮点数规格化表示

详解 浮点数的规格化表示_Hello.Aaric的博客-CSDN博客_浮点数规格化

浮点数表示_shuzfan的专栏-CSDN博客_浮点数

IEEE754 浮点数的表示方法_Dablelv的博客专栏-CSDN博客_ieee 754

二进制小数和IEEE浮点标准

标签：博客专栏   details   net   注意   因此   tail   load   --   技术   

原文地址：https://www.cnblogs.com/harrylyx/p/13234535.html