标签:编号 打开 细节 位置 没有 names break 死循环 超级
今天超级大水题,只是可惜了我之前的关路灯题解,白写了那么详细,结果考试还是没想起来……下边来分析一下今天的一些题目。
身为火影的纲手大人,当然不能眼睁睁地看着斑等一伙人胡作非为,木叶的全体忍者都信任身兼死神与忍者双重身份的你,相信你可以拯救世界,但是作为资深忍者的卡卡西同学向纲手大人提出建议,他想考验你作为忍者的基本能力---侦查。
斑在木叶周围建设了许多聚点,每一个聚点内都会藏有斑的手下。有些聚点是可以连通的。阴险的斑把所有连通的聚点作为他的一个基地,以便发动对木叶的总攻。卡卡西会告诉你每个聚点的藏敌人数和聚点的连通情况,他让你找出包含聚点数最多的基地,与包含敌人数目最多的基地。
\(n,m\)(\(n\) 为据点数,聚点编号为\(1...n,m\)为边数,\(n,m \le 500\));
接下的一行为\(n\)个整数,为每个聚点的藏敌人数,用空格相隔,敌数\(\le 1000\)。
接下来\(m\)行,每行两个数\(u,v\),表示\(u\)和\(v\)有边相连。
第一行为包含聚点数最多的基地内的聚点编号,以升序输出。
第二行为藏敌人数最多的基地内的聚点编号,以升序输出。
注意:若求得的两个基地包含的聚点数相同或藏敌数相同,则输出字典序最小的。
12 11
10 11 2 3 4 5 1 1 1 1 1 1
1 2
2 3
1 3
4 5
5 6
6 7
8 9
9 12
11 12
10 11
8 10
8 9 10 11 12
1 2 3
其实没啥好分析的,直接双向建边\(Tarjan\)求强联通分量,然后记录一下每个分量的人数和大小就行
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e3+10;
int head[maxn];
vector<int>scc[maxn];
struct Node{
int v,next;
}e[maxn<<1];
int c[maxn];
int n,m,val[maxn];
int siz[maxn];
int sum[maxn],jl1[maxn],jl2[maxn];
int dfn[maxn],low[maxn],num,tot,cnt;
int sta[maxn],top;
int vis[maxn];
void Add(int x,int y){
e[++tot].v = y;
e[tot].next = head[x];
head[x] = tot;
}
void Tarjan(int x){
dfn[x] = low[x] = ++num;
vis[x] = 1;
sta[++top] = x;
for(int i=head[x];i;i=e[i].next){
int v = e[i].v;
if(!dfn[v]){
Tarjan(v);
low[x] = min(low[x],low[v]);
}
else if(vis[v]){
low[x] = min(low[x],dfn[v]);
}
}
if(dfn[x] == low[x]){
cnt++;
int y;
while(1){
y = sta[top--];
c[y] = cnt;
siz[cnt]++;
sum[cnt]+=val[y];
vis[y] = 0;
scc[cnt].push_back(y);
if(x == y)break;
}
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i){
scanf("%d",&val[i]);
}
for(int i=1;i<=m;++i){
int x,y;
scanf("%d%d",&x,&y);
Add(x,y);
Add(y,x);
}
for(int i=1;i<=n;++i){
if(!dfn[i])Tarjan(i);
}
int jlsum,jljud;
int maxsum = 0;
int maxjud = 0;
for(int i=1;i<=cnt;++i){
if(maxsum<sum[i]){
jlsum = i;
maxsum = sum[i];
}
if(maxjud<scc[i].size()){
jljud = i;
maxjud = scc[i].size();
}
}
int dd = 0,ff = 0;
for(int i=0;i<scc[jlsum].size();i++){
jl1[++dd] = scc[jlsum][i];
}
for(int i=0;i<scc[jljud].size();i++){
jl2[++ff] = scc[jljud][i];
}
sort(jl1+1,jl1+dd+1);
sort(jl2+1,jl2+ff+1);
for(int i=1;i<=ff;i++){
printf("%d ",jl2[i]);
}
printf("\n");
for(int i=1;i<=dd;++i){
printf("%d ",jl1[i]);
}
printf("\n");
return 0;
}
\(Dilhao\)一共有\(n\)本教科书,每本教科书都有一个难度值,他每次出题的时候都会从其中挑两本教科书作为借鉴,如果这两本书的难度相差越大,\(Dilhao\)出的题就会越复杂,也就是说,一道题的复杂程度等于两本书难度差的绝对值。
这次轮到\(ldxxx\)出题啦,他想要管\(Dilhao\)借\(m\)本书作为参考去出题,\(Dilhao\)想知道,如果\(ldxxx\)在\(Dilhao\)给出的\(m\)本书里挑选难度相差最小的两本书出题,那么\(ldxxx\)出的题复杂程度最大是多少?
第一行是\(n\)和\(m\)。
接下来的\(n\)行,每行一个整数\(a_i\)表示第\(i\)本书的难度。
一个整数为\(ldxxx\)出的题复杂程度的最大值。
6 3
5
7
1
17
13
10
7
\(Dilhao\)给了\(ldxxx\)难度为\(1,10,17\)的三本书,\(ldxxx\)挑选难度为\(10\)和\(17\)的两本书,出题复杂度为\(7\);
如果\(Dilhao\)给出其他任何三本书,其中的两本书难度差的最小值都小于\(7\),所以\(ldxxx\)出题最大的复杂程度为\(7\)。
对于 \(30\%\)的数据: \(2\le n\le 20\);
对于 \(60\%\)的数据: \(2\le n\le 1000\);
对于 \(100\%\)的数据: \(2\le n\le 100000\), \(2 \le m\le n\), \(0\le a_i \le 1000000000\)。
看到标志性的最小中的最大,(有得题是最大中的最小)肯定就是二分答案了,主要就是判断。
因为是要求出差值的最大,所以我们就使用差分数组\(cf\)来记录排序后的两两之间的难度差。然后判断一下能否选出来\(m\)个就好了。下边看代码
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5+10;
int Max,a[maxn];
int n,m;
int cf[maxn];//差分数组
bool check(int x){
int cnt = 0,ch = 0;//cnt为几本书,ch为最大差值
for(int i=1;i<=n;++i){//枚举每一本书
ch += cf[i];//累加差值
if(ch>=x){//差值比当前扫描到的答案大就书加一,差值置为0
cnt++;
ch = 0;
}
}
if(cnt>=m-1)return true;//最终能够选出m个书就为真
return false;
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;++i){
cin>>a[i];
Max = max(Max,a[i]);//记录最大值
}
sort(a+1,a+n+1);//排序
for(int i=1;i<=n;++i){//记录差值
cf[i] = a[i+1]-a[i];
}
int l=0,r=Max;//从0到最大值二分
while(l<=r){
int mid = (l+r)>>1;
if(r-l == 1){//只差一就判断一下,不然会死循环
if(check(r) == true){//r能行就变成把l变成r,因为最后答案为l
l = r;
}
break;
}
if(check(mid) == true){//中间符合要求就向右转移
l = mid;
}
else r=mid;//否则向左
}
printf("%d\n",l);
}
\(zhclk\)已经坚信自己就是传说中的有缘人,于是,带着梦想,带着希冀,带着勇气,来到了神迹,寻找……
如下图,神迹的城堡是一个树形的结构,共有 \(n\)间屋子。每间屋子都有一把锁,并且每间屋子最多可以到另外的两个屋子里(它是一棵二叉树)。在城堡的每个房间都存在着不同的宝藏。现在 \(zhclk\) 站在城堡的大门口(\(1\) 号屋子门口)拥有 \(k\)把万能钥匙,可以打开任意一把锁,但每把钥匙只能用一次,钥匙是拔不出来的。
问题哪有那么简单……,\(Zhclk\)还有一个传送门,可以在任何时候带他去任何一间屋子,但传送门也只能 使用一次。
地图上画出了宝藏的分布,只有获得最大价值的宝藏 \(zhclk\)的目的才能实现。
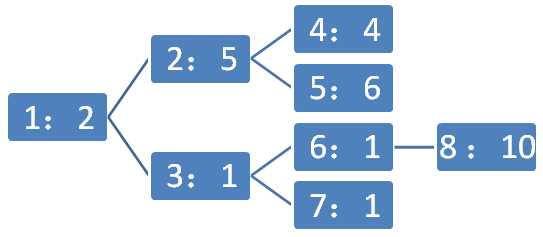
第一行:两个数 \(n\)和\(k\)。为城堡的屋子总数和你拥有的万能钥匙数。
第二行到第 \(n\)行:每行两个数 \(x_1\) 和 \(x_2\),为树上的 \(n?1\) 条边。(树保证以 \(1\)为根节点)。
第 \(n+1\)行:\(n\) 个数,第 \(i\) 个数为房间 \(i\) 的宝藏价值 \(v_i\) 。
一个数,为最大宝藏价值 \(maxv\)。
8 4
1 2
1 3
2 4
2 5
3 6
3 7
6 8
2 5 1 4 6 1 1 10
27
用钥匙依次开\(1,2,4,5\)号房间,再用传送门去 \(8\) 号房间,\(27=2+5+6+4+10\)
题目中u有个传送门,所以裸的树规肯定是要爆掉的。假设使用传送门从 \(x\) 到 \(y\),那么就有下边的结论:
\(y\)仅限于没有访问过的节点,当然更不是 \(x\)的祖先。可以将 \(y\)从整棵树中独立出来求值,并且这样做是正确的。
可以规定传送到 \(y\)之后不能再往祖先方向走,也就是把这部分断开。在 \(x\)节点使用传送门相当于回到 \(x\) 的任意一个祖先之后再使用传送门。因此,可以建立一个虚根\(n+1\)使用传送门,再令\(1\)为 \(n+1\)的左儿子,那么整棵树(除去\(y\))的值就都好计算了。
既然要把 \(y\)独立出去计算其值,那么可以令\(y\) 为 \(n+1\)的右儿子。
有了以上结论,很容易就可以开展树规了。
首先令 \(n+1\)的左儿子为 \(1\),然后从 \(2\) 到 \(n\)枚举 \(y\) (也就是传送到的节点),把 \(y\) 设置为 \(n+1\)的右儿子,对树\(n+1\)进行一次树形\(dp\)。
其中还有许多小细节,代码注释见
#include<bits/stdc++.h>
using namespace std;
const int maxn = 20+5;
int n,k,a[maxn],ans = 0;
int fa[maxn],ls[maxn],rs[maxn];
int dfs(int x,int sum){//树形dp
if(x==0)return 0;//没有点就返回0
if(sum==1)return a[x];//就一个钥匙了就返回权值,因为我们开一个传送门的时候加了一个边,也就是加了一个钥匙。
int now=0;//答案值
for(int i=0;i<sum;++i)
now=max(now,dfs(ls[x],i)+dfs(rs[x],sum-1-i)+a[x]);//从左儿子和右儿子递归
return now;
}
int main(){
scanf("%d%d",&n,&k);
for(int i=1;i<n;++i){
int x,y;
scanf("%d%d",&x,&y);
if(!ls[x])ls[x] = y;//第一个点为左儿子
else rs[x] = y;
fa[y] = x;//记录每个点的父亲节点
}
for(int i=1;i<=n;++i){
scanf("%d",&a[i]);
}
ls[n+1]=1;//虚根n+1
for(int i=2;i<=n;++i){
rs[n+1] = i;//一一枚举传送门到哪个点,让他为右儿子
if(ls[fa[i]] == i){//i父亲的左儿子是i就把左边断开,然后树归
ls[fa[i]] = 0;
ans = max(dfs(n+1,k+2),ans);
ls[fa[i]] = i;//这次递归完以后再连上
}
else {//右儿子跟左儿子一样
rs[fa[i]] = 0;
ans = max(ans,dfs(n+1,k+2));
rs[fa[i]] = i;
}
}
cout<<ans<<endl;//输出最大值
}
这个题的名字真的是没谁了,也不知道谁想的。原题(虽然当时我忘了),具体分析见之前我的博客:关路灯。
在一个数轴上,有 \(n\) 个 \(MM\) 在哭泣(5555~一直哭)。
\(tcboy\)也在这个数轴上,并恰好看到了这一幕,由于每个\(MM\)哭都会让\(tcboy\)损失一定的\(rp\),于是\(tcboy\)有必要去安慰她们(真命苦啊T.T)。
开始时,\(tcboy\)站在 \(k\) 号 \(MM\)的旁边。
现在知道第 \(i\) 个 \(MM\) 哭泣每秒钟会使\(tcboy\) 降低 \(w_i\) 的 \(rp\) (单位 \(rp\)/\(s\))。而 \(tcboy\)的行走速度很慢,只有\(1m\)/\(s\) 。\(tcboy\) 安慰 \(MM\)的方式很特别,不需要花费时间。请计算\(tcboy\)安慰完所有 \(MM\),会消耗掉的 \(rp\)的最小值。
第一行包含一个整数 \(N,2\le N\le 1000\),表示 \(MM\)的数量。
第二行包含一个整数 \(V,1\le V\le N\),表示开始时 \(tcboy\) 站在几号 \(MM\)的旁边。
接下来的 \(N\)行中,每行包含两个用空格隔开的整数 \(D\) 和 \(W\),用来描述每个 \(MM\),其中\(0\le D\le 1000,0\le W\le 1000\)。\(D\) 表示 \(MM\) 在数轴上的位置(单位: \(m\)),\(W\) 表示每秒钟会使 \(tcboy\) 降低\(W\) 的 \(rp\) 。
输出只有一行:一个整数,即消耗 \(rp\)之和的最小值。
结果不超过 \(10^9\) 。
4
3
2 2
5 8
6 1
8 7
56
之前博客链接:https://www.cnblogs.com/Vocanda/p/13184264.html
标签:编号 打开 细节 位置 没有 names break 死循环 超级
原文地址:https://www.cnblogs.com/Vocanda/p/13236199.html