378. 有序矩阵中第K小的元素

标签：vector   结果   简单   计算   img   lazy   答案   alt   初始   

给定一个 n x n 矩阵，其中每行和每列元素均按升序排序，找到矩阵中第 k 小的元素。
请注意，它是排序后的第 k 小元素，而不是第 k 个不同的元素。

示例：

matrix = [
[ 1, 5, 9],
[10, 11, 13],
[12, 13, 15]
],
k = 8,

返回 13。

解:这个题很有意思，找的不是某个数而是第k小的，这就不能简单的定个点周围找了，可以参考二分查找

我们只要沿着这条锯齿线走一遍即可计算出这两个板块的大小，也自然就统计出了这个矩阵中不大于 midmid 的数的个数了。

走法演示如下，取 mid=8mid=8：

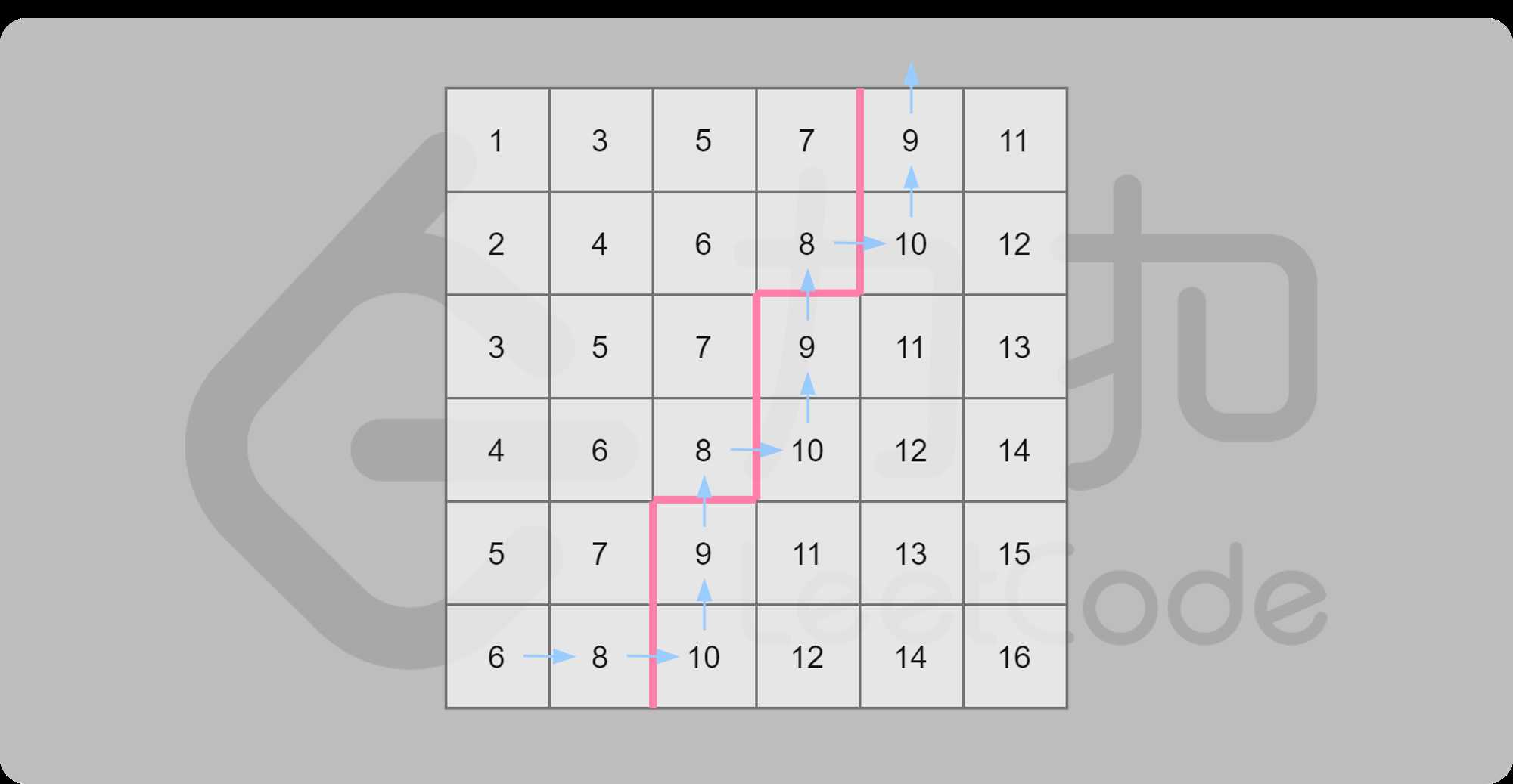
初始位置在 matrix[n - 1][0]matrix[n−1][0]（即左下角）；

设当前位置为 matrix[i][j]matrix[i][j]。若 matrix[i][j] \leq midmatrix[i][j]≤mid，则将当前所在列的不大于 midmid 的数的数量（即 i + 1i+1）累加到答案中，并向右移动，否则向上移动；

不断移动直到走出格子为止。

我们发现这样的走法时间复杂度为 O(n)O(n)，即我们可以线性计算对于任意一个 midmid，矩阵中有多少数不大于它。这满足了二分查找的性质。

不妨假设答案为 xx，那么可以知道 l\leq x\leq rl≤x≤r，这样就确定了二分查找的上下界。

每次对于「猜测」的答案 midmid，计算矩阵中有多少数不大于 midmid ：

如果数量不少于 kk，那么说明最终答案 xx 不大于 midmid；
如果数量少于 kk，那么说明最终答案 xx 大于 midmid。
这样我们就可以计算出最终的结果 xx 了。

class Solution {
   public:
    bool check(vector<vector<int>>& matrix, int mid, int k, int n) {
        int i = n - 1;
        int j = 0;
        int num = 0;
        while (i >= 0 && j < n) {
            if (matrix[i][j] <= mid) {
                num += i + 1;
                j++;
            } else {
                i--;
            }
        }
        return num >= k;
    }

    int kthSmallest(vector<vector<int>>& matrix, int k) {
        int n = matrix.size();
        int left = matrix[0][0];
        int right = matrix[n - 1][n - 1];
        while (left < right) {
            int mid = left + ((right - left) >> 1);
            if (check(matrix, mid, k, n)) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }
};

378. 有序矩阵中第K小的元素

标签：vector   结果   简单   计算   img   lazy   答案   alt   初始   

原文地址：https://www.cnblogs.com/wangshaowei/p/13236383.html