标签:style blog class code c tar
这篇文章是对《算法导论》上Prim算法求无向连通图最小生成树的一个总结,其中有关于我的一点点小看法。
最小生成树的具体问题可以用下面的语言阐述:
输入:一个无向带权图G=(V,E),对于每一条边(u,
v)属于E,都有一个权值w。
输出:这个图的最小生成树,即一棵连接所有顶点的树,且这棵树中的边的权值的和最小。
举例如下,求下图的最小生成树:
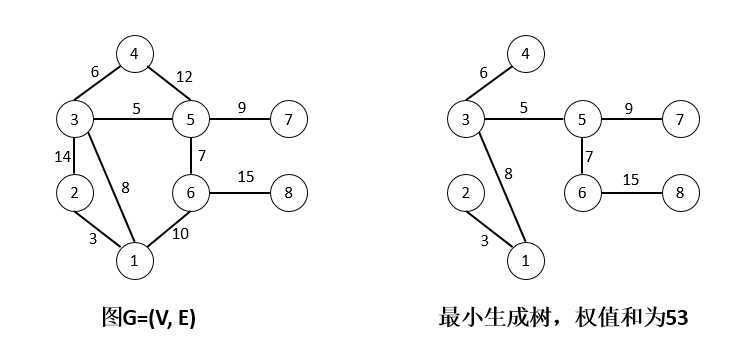
这个问题是求解一个最优解的过程。那么怎样才算最优呢?
首先我们考虑最优子结构:如果一个问题的最优解中包含了子问题的最优解,则该问题具有最优子结构。
最小生成树是满足最优子结构的,下面会给出证明:
最优子结构描述:假设我们已经得到了一个图的最小生成树(MST) T,(u, v)是这棵树中的任意一条边。如图所示:
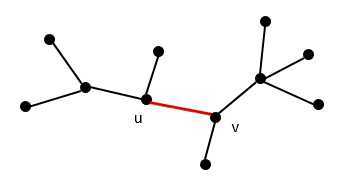
现在我们把这条边移除,就得到了两科子树T1和T2,如图:
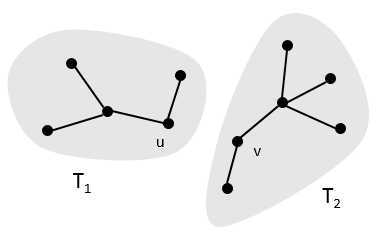
T1是图G1=(V1, E1)的最小生成树,G1是由T1的顶点导出的图G的子图,E1={(x, y)∈E, x, y ∈V1}
同理可得T2是图G2=(V2, E2)的最小生成树,G2是由T2的顶点导出的图G的子图,E2={(x, y)∈E, x, y ∈V2}
现在我们来证明上述结论:使用剪贴法。w(T)表示T树的权值和。
首先权值关系满足:w(T) = w(u, v)+w(T1)+w(T2)
假设存在一棵树T1‘比T1更适合图G1,那么就存在T‘={(u,v)}UT1‘UT2‘,那么T‘就会比T更适合图G,这与T是最优解相矛盾。得证。
因此最小生成树具有最优子结构,那么它是否还具有重叠子问题性质呢?我们可以发现,不管删除那条边,上述的最优子结构性质都满足,都可以同样求解,因此是满足重叠子问题性质的。
考虑到这,我们可能会想:那就说明最小生成树可以用动态规划来做咯?对,可以,但是它的代价是很高的。
我们还能发现,它还有个更强大的性质:贪心选择性质。因而可用贪心算法完成。
贪心算法特点:一个局部最优解也是全局最优解。
最小生成树的贪心选择性质:令T为图G的最小生成树,另A?V,假设边(u, v)∈E是连接着A到A的补集(也就是V-A)的最小权值边,那么(u, v)属于最小生成树。
证明:假设(u, v)?T, 使用剪贴法。现在对下图进行分析,图中A的点用空心点表示,V-A的点用实心点表示:
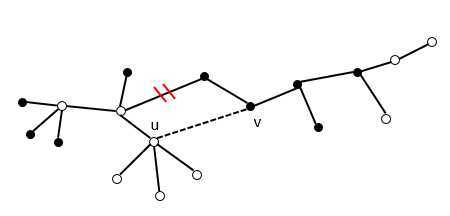
在T树中,考虑从u到v的一条简单路径(注意现在(u, v)不在T中),根据树的性质,它是唯一的。
现在把(u, v)和这条路上中的第一条连接A和V-A的边交换,即画红杠的那条边,边(u, v)是连接A和V-A的权值最小边,那我们就得到了一棵更小的树,这就与T是最小 生成树矛盾。得证。
现在呢,我们来看看Prim的思想:Prim算法的特点是集合E中的边总是形成单棵树。树从任意根顶点s开始,并逐渐形成,直至该树覆盖了V中所有顶点。每次添加到树中的边都是使树的权值尽可能小的边。因而上述策略是“贪心”的。
算法的输入是无向连通图G=(V, E)和待生成的最小生成树的根r。在算法的执行过程中,不在树中的所有顶点都放在一个基于key域的最小优先级队列Q中。对每个顶点v来说,key[v]是所有将v与树中某一顶点相连的边中的最小权值;按规定如果不存在这样的边,则key[v]=∞。
实现Prim算法的伪代码如下所示:
MST-PRIM(G, w, r)
for each u∈V
do key[u] ← ∞
parent[u]← NIL
key[r] ← 0
Q ← V
while Q ≠?
do u ← EXTRACT-MIN(Q)
for each v∈Adj[u]
do if v∈Q and w(u, v) < key[v]
then parent[v] ← u
key[v] ← w(u, v)
其工作流程为:
(1)首先进行初始化操作,将所有顶点入优先队列,队列的优先级为权值越小优先级越高
(2)取队列顶端的点u,找到所有与它相邻且不在树中的顶点v,如果w(u, v) < key[v],说明这条边比之前的更优,加入到树中,即更改父节点和key值。这中间还 隐含着更新Q的操作(降key值)
(3)重复2操作,直至队列空为止。
(4)最后我们就得到了两个数组,key[v]表示树中连接v顶点的最小权值边的权值,parent[v]表示v的父结点。
现在呢,我们发现一个问题,这里要用到优先队列来实现这个算法,而且每次搜索邻接表都要进行队列更新的操作。
不管用什么方法,总共用时为O(V*T(EXTRACTION)+E*T(DECREASE))
(1)如果用数组来实现,总时间复杂度为O(V2)
(2)如果用二叉堆来实现,总时间复杂度为O(ElogV)
(3)如果使用斐波那契堆,总时间复杂度为O(E+VlogV)
上面的三种方法,越往下时间复杂度越好,但是实现难度越高,而且每次对最小优先队列的更新是非常麻烦的,那么,有没有一种方法,可以不更新优先队列也达到同样的 效果呢?
答案是:有。
其实只需要简单的操作就可以达到。首次只将根结点入队列。第一次循环,取出队列顶结点,将其退队列,之后找到队列顶的结点的所有相邻顶点,若有更新,则更新它们的key值后,再将它们压入队列。重复操作直至队列空为止。因为对树的更新是局部的,所以只需将相邻顶点key值更新即可。push操作的复杂度为O(logV),而且省去了之前将所有顶点入队列的时间,因而总复杂度为O(ElogV)。
具体实现代码,优先队列可以用STL实现:

1 #include <iostream> 2 #include <cstdio> 3 #include <vector> 4 #include <queue> 5 using namespace std; 6 7 #define maxn 100 //最大顶点个数 8 int n, m; //顶点数,边数 9 10 struct arcnode //边结点 11 { 12 int vertex; //与表头结点相邻的顶点编号 13 int weight; //连接两顶点的边的权值 14 arcnode * next; //指向下一相邻接点 15 arcnode() {} 16 arcnode(int v,int w):vertex(v),weight(w),next(NULL) {} 17 }; 18 19 struct vernode //顶点结点,为每一条邻接表的表头结点 20 { 21 int vex; //当前定点编号 22 arcnode * firarc; //与该顶点相连的第一个顶点组成的边 23 }Ver[maxn]; 24 25 void Init() //建立图的邻接表需要先初始化,建立顶点结点 26 { 27 for(int i = 1; i <= n; i++) 28 { 29 Ver[i].vex = i; 30 Ver[i].firarc = NULL; 31 } 32 } 33 34 void Insert(int a, int b, int w) //插入以a为起点,b为终点,权为w的边 35 { 36 arcnode * q = new arcnode(b, w); 37 if(Ver[a].firarc == NULL) 38 Ver[a].firarc = q; 39 else 40 { 41 arcnode * p = Ver[a].firarc; 42 q->next = p; 43 Ver[a].firarc = q; 44 } 45 } 46 47 struct node //保存key值的结点 48 { 49 int v; 50 int key; 51 friend bool operator<(node a, node b) //自定义优先级,key小的优先 52 { 53 return a.key > b.key; 54 } 55 }; 56 57 #define INF 9999 //权值上限 58 int parent[maxn]; //每个结点的父节点 59 bool visited[maxn]; //是否已经加入树种 60 node vx[maxn]; //保存每个结点与其父节点连接边的权值 61 priority_queue<node> q; //优先队列stl实现 62 void Prim(int s) //s表示根结点 63 { 64 for(int i = 1; i <= n; i++) //初始化 65 { 66 vx[i].v = i; 67 vx[i].key = INF; 68 parent[i] = -1; 69 visited[i] = false; 70 } 71 vx[s].key = 0; 72 q.push(vx[s]); 73 while(!q.empty()) 74 { 75 node nd = q.top(); //取队首,记得赶紧pop掉 76 visited[nd.v] = true; 77 q.pop(); 78 arcnode * p = Ver[nd.v].firarc; 79 while(p != NULL) //找到所有相邻结点,若未访问,则入队列 80 { 81 if(!visited[p->vertex] && p->weight < vx[p->vertex].key) 82 { 83 parent[p->vertex] = nd.v; 84 vx[p->vertex].key = p->weight; 85 vx[p->vertex].v = p->vertex; 86 q.push(vx[p->vertex]); 87 } 88 p = p->next; 89 } 90 91 } 92 } 93 94 int main() 95 { 96 int a, b ,w; 97 cout << "输入n和m: "; 98 cin >> n >> m; 99 Init(); 100 cout << "输入所有的边:" << endl; 101 while(m--) 102 { 103 cin >> a >> b >> w; 104 Insert(a, b, w); 105 Insert(b, a, w); 106 } 107 Prim(1); 108 cout << "输出所有结点的父结点:" << endl; 109 for(int i = 1; i <= n; i++) 110 cout << parent[i] << " "; 111 cout << endl; 112 cout << "最小生成树权值为:"; 113 int cnt = 0; 114 for(int i = 1; i <= n; i++) 115 cnt += vx[i].key; 116 cout << cnt << endl; 117 return 0; 118 }
运行结果如下(基于第一个例子):
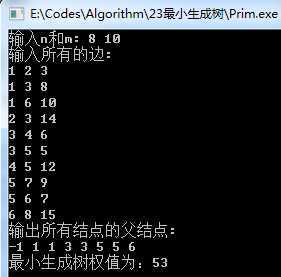
望支持,谢谢。
图基本算法 最小生成树 Prim算法(邻接表+优先队列STL),布布扣,bubuko.com
图基本算法 最小生成树 Prim算法(邻接表+优先队列STL)
标签:style blog class code c tar
原文地址:http://www.cnblogs.com/dzkang2011/p/prim_1.html