奇怪|说好的求最大值变成了求最小值

标签：doc   mbed   math   img   tps   mos   题目   最大   idt   

前言

大千世界，无奇不有，明明题目说好的求最大值，到最后却变成了求最小值。看来凡事，总有个例外，不能太绝对了。

探究案例

例1【2020北京人大附中高一试题】如图所示，一条直角走廊宽为\(a(a>0)\)，

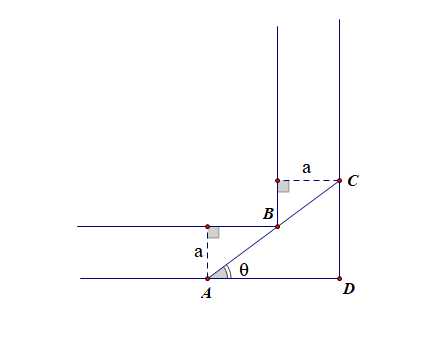
(1).若位于水平地面上的一根铁棒在此直角走廊内，且\(\angle BAD=\theta\)，试求铁棒的长\(l\)；

分析：\(l=AB+BC=\cfrac{a}{\sin\theta}+\cfrac{a}{\cos\theta}\)，\(\theta\in [0,\cfrac{\pi}{2}]\)；

(2).若一根铁棒能水平地通过此直角走廊，求此铁棒的最大长度；

分析：由(1).可知，即求\(l=l(\theta)=\cfrac{a}{\sin\theta}+\cfrac{a}{\cos\theta}\)，\(\theta\in [0,\cfrac{\pi}{2}]\)的最大值[一般都这样理解，不过此处有坑]；

则\(l=a\times \cfrac{\sin\theta+\cos\theta}{\sin\theta\cdot\cos\theta}\)，\(\theta\in [0,\cfrac{\pi}{2}]\)

令\(t=\sin\theta+\cos\theta=\sqrt{2}\sin(\theta+\cfrac{\pi}{4})\in[1, \sqrt{2}]\)，

则由\((\sin\theta+\cos\theta)^2=t^2\)，解得\(\sin\theta\cdot\cos\theta=\cfrac{t^2-1}{2}\)，

故\(l(\theta)=a\times \cfrac{t}{\frac{t^2-1}{2}}=a\times \cfrac{2t}{t^2-1}=2a\times \cfrac{1}{t-\frac{1}{t}}=f(t)\)，\(t\in[1, \sqrt{2}]\)

则转化为求\(f(t)\)的最大值，令\(g(t)=t-\cfrac{1}{t}\)，\(g‘(t)=1+\cfrac{1}{t^2}>0\)在\(t\in[1, \sqrt{2}]\)上恒成立，

故\(f(t)_{max}=f(1)\rightarrow +\infty\)，显然不合适了，出了问题；

那么我们结合实际问题想，其实本问题所求的最大值应该转换为函数\(f(t)\)的最小值；

[备注：从铁棒的长度为无穷长逐步缩小，当缩小到一个合适的长度时，此时刚好刚刚水平通过，再从另一个角度，让铁棒的长度从零开始逐步增大，当增大到一个合适的长度时，此时刚好刚刚水平通过，到此，我们艰难的迈过了此题目中的坑]；

这样\(f(t)_{min}=f(\sqrt{2})=2a\times \cfrac{1}{\sqrt{2}-\frac{1}{\sqrt{2}}}=2\sqrt{2}a\)；

故铁棒能水平地通过此直角走廊的最大长度为\(2\sqrt{2}a\)；

引申：或从形上思考，结合给定的直角走廊的对称性，当\(\theta=\cfrac{\pi}{4}\)时，此时的铁棒的长度即为所求的能顺利通过直角走廊的最大值，也可以计算得到\(l_{max}=2\sqrt{2}a\)；

数学游戏

气氛太沉闷严谨，做个数学实验小游戏看看。

(3).如图所示，现有一辆转动灵活的平板车，其平板面是矩形，它的宽\(AD=b(0<b<a)\)，平板车若想顺利通过直角走廊，其长度\(l\)不能超过多少米？

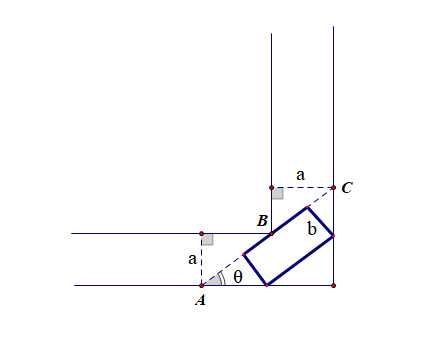
分析：平板车的长度为\(l=\cfrac{a}{\sin\theta}+\cfrac{a}{\cos\theta}-\cfrac{b}{\tan\theta}-b\times \tan\theta\)

\(=a\times \cfrac{\sin\theta+\cos\theta}{\sin\theta\cdot\cos\theta}-b\times \cfrac{\sin^2\theta+\cos^2\theta}{\sin\theta\cdot\cos\theta}\)

\(=\cfrac{a(\sin\theta+\cos\theta)-b}{\sin\theta\cdot\cos\theta}\)，\(\theta\in [0,\cfrac{\pi}{2}]\)

令\(t=\sin\theta+\cos\theta=\sqrt{2}\sin(\theta+\cfrac{\pi}{4})\in[1, \sqrt{2}]\)，

则由\((\sin\theta+\cos\theta)^2=t^2\)，解得\(\sin\theta\cdot\cos\theta=\cfrac{t^2-1}{2}\)，

则\(l=\cfrac{at-b}{\frac{t^2-1}{2}}=\cfrac{2at-2b}{t^2-1}=h(t)\)， \(t\in[1, \sqrt{2}]\)，\(0<b<a\)，

则\(l=h(t)=\cfrac{2at-2a+2a-2b}{t^2-1}=\cfrac{2a}{t+1}+\cfrac{2a-2b}{t^2-1}\) ^[1]

由于\(y=\cfrac{2a}{t+1}\)在\(t\in[1, \sqrt{2}]\)单调递减，\(y=\cfrac{2a-2b}{t^2-1}\)在\(t\in[1, \sqrt{2}]\)单调递减，

故\(l_{min}=h(t)_{min}=h(\sqrt{2})=2\sqrt{2}a-2b\)，[此问同样存在最大值与最小值的转化]

故平板车若想顺利通过直角走廊，长度\(l\)不能超过\(2\sqrt{2}a-2b\)米.

奇怪|说好的求最大值变成了求最小值

标签：doc   mbed   math   img   tps   mos   题目   最大   idt   

原文地址：https://www.cnblogs.com/wanghai0666/p/13253416.html