84. 柱状图中最大的矩形（Largest Rectangle in Histogram）

标签：提交   rectangle   rect   mic   最大的   暴力   面积   class   span   

题目描述：

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

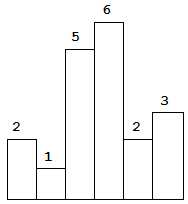
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

示例:

输入: [2,1,5,6,2,3]
输出: 10

解题思路：

　　这道题暴力解法就是依次遍历每根柱子，以这根柱子的高度为最小值，向左和向右寻找边界，即寻找第一个比该柱子低的柱子。这时左边界和右边界围起来的宽度乘以该柱子的高度就等于以这根柱子的高度为最小值的矩形的面积。依次枚举所有的柱子就可以得到面积的最大值，时间复杂度为O(n2)，提交暴力解法会超时。

　　这道题有O(n)的解法，就是使用单调栈。总的思路是遍历三次数组，第一次遍历得到每根柱子对应矩形的左边界，第二次遍历得到每根柱子对应矩形的右边界，第三次遍历得到最后的答案。左右边界的定义和暴力解法中的相同。那么如何用单调栈完成这个过程呢？

　　比如第一次遍历中，从左到右开始遍历，假设此时遍历的下标为i。寻找i的左边界，就是寻找第一个小于heights[i]且位于i的左边的柱子。注意到我们遍历到i时，其实i左边的所有柱子都是遍历过的，那么就可以想到在遍历时就要记录下有用的信息，当遍历到i时可以直接使用该信息。想象一下，当从0开始遍历到i的过程，如果左边的柱子比右边的柱子高，那么左边的这根柱子一定是没用的。如果右边的柱子小于heights[i]，那此时就已经终止了，所以不会考虑左边的柱子；当右边的柱子大于等于heights[i]时，那么左边的柱子一定也大于等于heights[i]，所以第一个小于heights[i]的柱子（左边界）一定也不是它。综合下来就是只用保存左边的柱子比右边柱子小的情况。再接着往下思考，新加入一个柱子时，按照同样的思路，应该把栈中所有比它高的柱子都pop出来，因为那些柱子已经没用了。而这时栈顶的元素就刚好是第一个小于新加入柱子的柱子，也就是要寻找的左边界。至此找到左边界的过程就结束了，因为每次加入新柱子，在保存信息的同时（入栈）也可以得到左边界，所以顺序遍历一遍heights数组，就可以得到每根柱子对应的左边界。

　　右边界同理可得，主要要从右往左遍历。最后只需要再遍历一次每根柱子，更新最大面积即可。当然也可以在遍历右边界时直接计算，不过这样的可读性稍微差一点。

　　注意当栈为空时，保存的下标应该是-1或者heights的尾后下标，这样在计算面积时可以使用同一个面积计算公式。

　　代码如下：

class Solution
{
public:
    int largestRectangleArea(vector<int>& heights)
    {
        stack<int> s;
        vector<int> left_bound(heights.size());
        for (int i = 0; i != heights.size(); ++i)
        {
            while (!s.empty() && heights[s.top()] >= heights[i])
                s.pop();
            left_bound[i] = s.empty() ? -1 : s.top();
            s.push(i);
        }

        s = stack<int>();
        vector<int> right_bound(heights.size());
        for (int i = heights.size() - 1; i >= 0; --i)
        {
            while (!s.empty() && heights[s.top()] >= heights[i])
                s.pop();
            right_bound[i] = s.empty() ? heights.size() : s.top();
            s.push(i);
        }

        int res = 0;
        for (int i = 0; i != heights.size(); ++i)
        {
            res = max(res, heights[i] * (right_bound[i] - left_bound[i] - 1));
        }
        return res;
    }
};

84. 柱状图中最大的矩形（Largest Rectangle in Histogram）

标签：提交   rectangle   rect   mic   最大的   暴力   面积   class   span   

原文地址：https://www.cnblogs.com/yxsrt/p/13254140.html