【生物信息】RPKM, FPKM和TPM

时间：2020-07-06 16:08:29 阅读：273 评论：0 收藏：0 [点我收藏+]

注：这几个名词是RNA-Seq数据分析中的基础，在此小结一下。

在RNA-Seq的分析中，对基因或转录本的read counts数目进行标准化（normalization）是一个极其重要的步骤，因为落在一个基因区域內的read counts数目取决于基因长度和测序深度。很容易理解：一个基因越长、测序深度越深，落在（比对到）该基因所在区域的read counts数目就会相对越多。当我们进行基因差异表达的分析时，往往是在多个样本中比较不同基因的表达量，如果不进行数据标准化，比较结果是没有意义的（因为差异可能是由于测序深度导致的，而不是本身表达上的差异）。因此，我们需要标准化的两个关键因素就是基因长度和测序深度，常常用RPKM (Reads Per Kilobase Million), FPKM (Fragments Per Kilobase Million) 和 TPM (Transcripts Per Million)作为标准化数值。

RPKM和FPKM

计算RPKM主要包括以下三步：

计算与测序深度有关的系数：计算每个样本中reads的总数并除以$10^6$——此时就可以得到"per million"的缩放系数；
去除测序深度的影响：每个reads数除以上面得到的"per million"缩放系数，得到对应基因在每百万reads中所占比例，即reads per million (RPM)；
去除基因长度的影响：用上一步的结果再除以对应基因的长度（通常是所有外显子长度的总和，以kb为单位），得到每百万reads每一千碱基对中包含的reads数，即RPKM。

计算RPKM的公式可以表示如下（如图1中的示例）：

$$RPKM(x)=\frac{Reads \ per \ transcript}{\frac{total \ reads}{10^6} \times \frac{transcript \ length}{1000}} = \frac{Reads \ per \ transcript}{million \ reads \times transcript \ length (kb)} = \frac{10^9 \times C_x}{R \times L_x} \quad \cdots (1)$$

其中：

x可以表示一个基因或转录本，或基因组上一段特定的区域（下面统一当做基因）；
$C_x$表示比对到基因x外显子区域的reads数；
R表示当前样本中包含的全部reads数，$R = \sum_{i=1}^{N} C_i$，其中N表示该样本中的基因总数；
$L_x$表示基因x外显子区域包含的碱基数（bp）.

技术图片

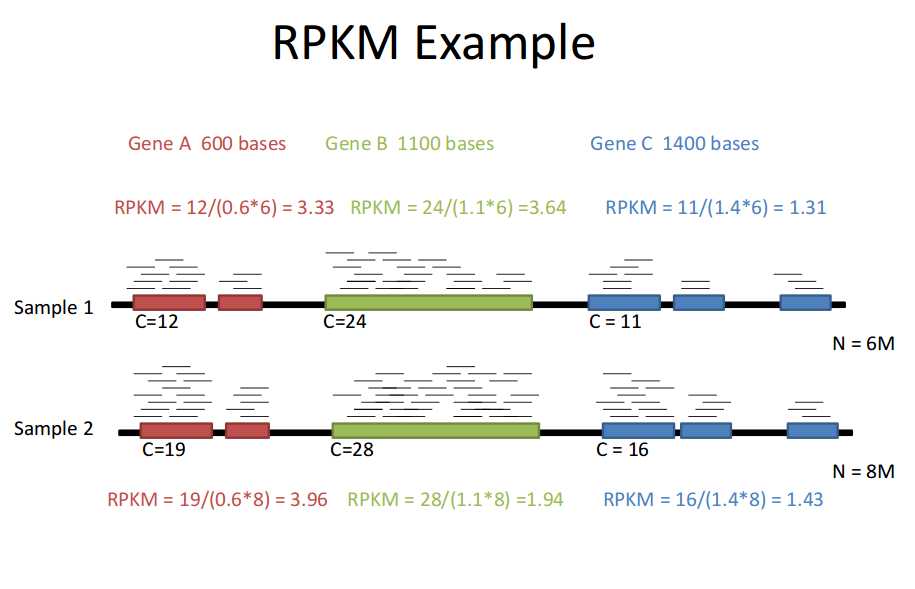
图1：RPKM的计算

FPKM与RPKM的计算过程相同，它们的区别是：RPKM用于单端测序结果，FPKM用于双端测序结果（如图2所示）。因为双端测序中，每一个fragment会包含两个reads，使用FPKM来计算基因的表达丰度时，可以避免把同一个fragment的两个reads计算两次（实际上只需要计算一次）。

技术图片

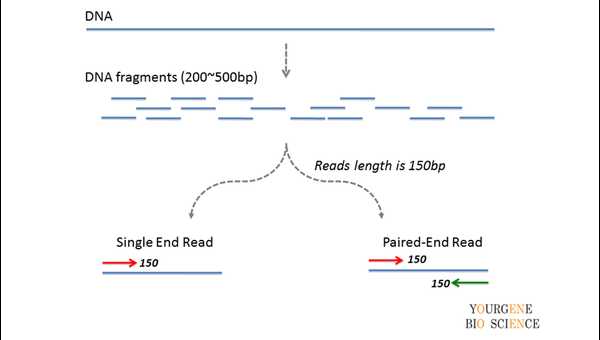
图2：单端测序read与双端测序read

单端read与双端read比对到基因组的示意图如图3所示：

技术图片

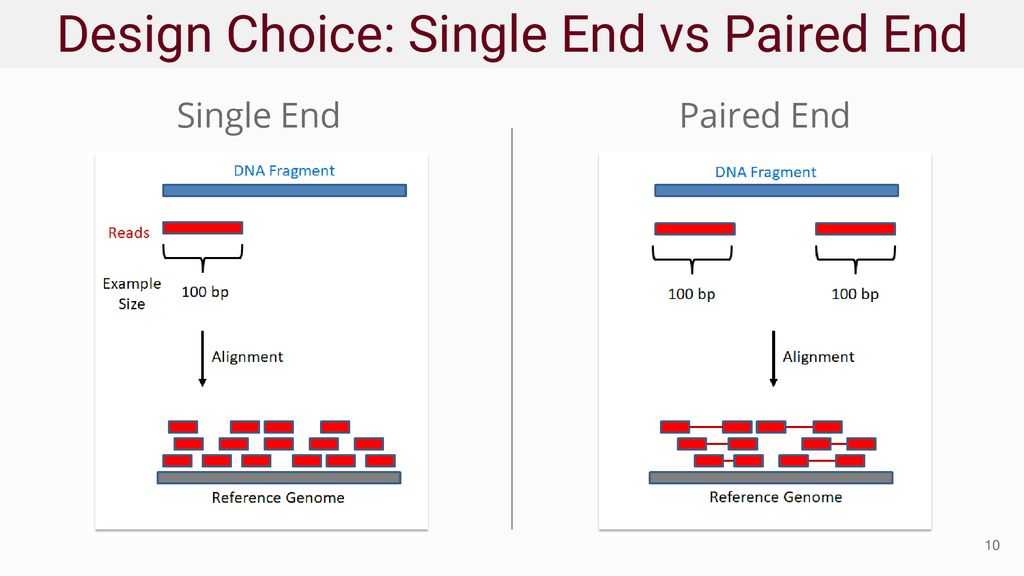
图3：单端测序read与双端测序read比对到参考基因组

TPM

TPM与RPKM最大的区别在于消除两种影响的次序：在TPM中先消除基因长度的影响，再消除测序深度的影响。计算TPM的过程也可以分为三个步骤：

将每个read counts除以对应基因的长度（外显子区域的长度，单位为kb），此时得到每千个碱基包含的reads数，即（reads per kilobase, RPK）；
将一个样本中的RPK加起来的总数除以$10^6$，得到"per million"缩放系数（这是两种方法计算结果不同的主要来源，因为这里的总数是消除了基因长度的影响之后得到的RPK，而不是原始read counts之和）；
用RPK除以"per million"缩放系数，得到TPM。

计算公式表示如下：

$$TPM(x) = \frac{C_x \times r \times 10^6}{L_x \times T} = \frac{C_x / L_x \times 10^6}{\sum_{i=1}^{N} C_i / L_i} \quad \cdots (2)$$

其中：

x可以表示一个基因或转录本，或基因组上一段特定的区域（下面统一当做基因）；
r表示reads的长度（例如所有reads包含的平均碱基数），一般为常数；
$C_x$表示比对到基因x外显子区域的reads数；
T表示当前样本中所有基因除以自身长度（kb）后求和的结果，$T = \sum_{i=1}^{N} r \times C_i / L_i$，其中N表示该样本中的基因总数；
$L_x$表示基因x外显子区域包含的碱基数（kp）.

因为交换了两次计算的次序，TPM最终得到的结果中，每个样本总的TPM值是相同的，这样的结果便于样本间差异的比较。

RPKM与TPM的比较

根据提出TPM的论文（Günter P. Wagner et al., 2012）中的介绍：从理论上来说，任意基因的表达量（$mRNA_x$）占样本中所有基因总的表达量（$mRNA_T$）比值（文中提到的相对摩尔浓度，$rmc$）的均值应该是一个固定的值。用公式可表示如下：

$$rmc_x = \frac{mRNA_x}{mRNA_T}$$

$$E[rmc] = \frac{1}{N} \sum_{i=1}^{N} \frac{mRNA_i}{mRNA_T} = \frac{1}{N} \frac{\sum_{i=1}^{N} mRNA_i}{mRNA_T} = \frac{1}{N}$$

其中：

x可以表示一个基因或转录本，或基因组上一段特定的区域（下面统一当做基因）；
$mRNA_x$表示基因x的表达量（丰度）；
$mRNA_T$表示所有基因在该样本中总的表达量；
N表示样本中包含的基因总数；
$E[rmc]$表示相对摩尔浓度的均值。

这里的均值与下面例子中的均值的含义相同：假设现在有100万元，20个人分，无论这些人怎么分，最终人均都是5万元，即$100/20$；人均占比都是$\frac{5}{100} = \frac{1}{20}$。上述相对摩尔浓度的均值就相当于这里的人均占比，只与人数有关。

由于以上的约束条件，我们在构造统计量对任意基因在某个样本中的相对表达丰度进行估计时，该估计量的均值也应该是一个只与基因总数相关的值。于是就有了对RPKM的反对以及TPM的提出。因为任意一个样本中所有基因的TPM之和都等于$10^6$，因此其均值都等于$\frac{10^6}{N}$。

计算RPKM和TPM的代码示例

下面展示Python代码：

 1 import pandas as pd
 2 import numpy as np
 3 
 4 
 5 def read_counts2tpm(df, sample_name):
 6     """
 7     convert read counts to TPM (transcripts per million)
 8     :param df: a dataFrame contains the result coming from featureCounts
 9     :param sample_name: a list, all sample names, same as the result of featureCounts
10     :return: TPM
11     """
12     result = df
13     sample_reads = result.loc[:, sample_name].copy()
14     gene_len = result.loc[:, [‘Length‘]]
15     rate = sample_reads.values / gene_len.values
16     tpm = rate / np.sum(rate, axis=0).reshape(1, -1) * 1e6
17     return pd.DataFrame(data=tpm, columns=sample_name, index=df[‘Gene‘])
18 
19 def read_counts2rpkm(df, sample_name):
20     result = df
21     sample_reads = result.loc[:, sample_name].copy()
22     gene_len = result.loc[:, [‘Length‘]]
23     total_reads = np.sum(sample_reads.values, axis=0).reshape(1, -1)
24     rate = sample_reads.values / gene_len.values
25     tpm = rate / total_reads * 1e6
26     return pd.DataFrame(data=tpm, columns=sample_name, index=df[‘Gene‘])

从代码上可以看到，计算RPMK与计算TPM的差别有两点，在RPKM中计算total_reads用的是原始reads数（第23行），且用该值来消除测序深度对结果的影响（第25行）；在TPM中，使用的是消除基因长度的影响之后的值来求和（第16行）。

下面通过示例数据来计算结果：

# raw data
a = pd.DataFrame(data = {
    ‘Gene‘: ("A","B","C","D","E"),
    ‘Length‘: (100, 50, 25, 5, 1),
     ‘S1‘: (80, 10,  6,  3,   1),
     ‘S2‘: (20, 20, 10, 50, 400)
})

tpm = read_counts2tpm(a, [‘S1‘, ‘S2‘])

rpkm = read_counts2rpkm(df=a, sample_name=[‘S1‘, ‘S2‘])

构造的示例数据包括基因名称、长度、样本1和样本2的read counts，该结果可以通过featureCounts等上游工具得到。

结果如下：

# TPM
Gene    S1              S2	
A	281690.140845	486.618005
B	70422.535211	973.236010
C	84507.042254	973.236010
D	211267.605634	24330.900243
E	352112.676056	973236.009732

# RPKM
Gene	S1	S2
A	8000.0	400.0
B	2000.0	800.0
C	2400.0	800.0
D	6000.0	20000.0
E	10000.0	800000.0

可以验证得到，在两个样本中TPM之和都等于$10^6$，且均值都等于200000。