标签:问题 查找 并且 inf 地球仪 hashmap 记忆 说明 ash
一、开门见山
1,二叉树是“平衡”的,查找效率才最高;也正是需要强大的约束,才方便二叉树后面的操作。
2,当二叉树不平衡时,就需要通过“树的旋转”让树恢复平衡,旋转两个字不知道是不是官方的说法,方便大家交流?以下的说明将不会从“旋转”入手,因为我觉得旋转只会把人转晕;下面将会从“拎起来某个节点”的角度说明问题,很多同学也是这么解释的。
3,树的旋转实在是很难记忆也很难使用语言使别人明白的事情(或者我缺乏这样的能力),所以下面的介绍适合想整明白“树的旋转”,但并不钻墙角的同学。
二、说明
1,LL型
即某个节点的左节点的左节点上再挂上一个节点,使树失去平衡,如下图:
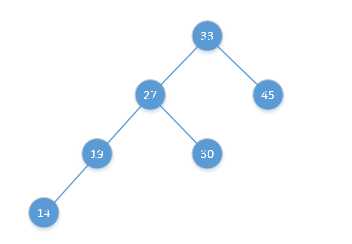
如果上面的图是真实的,节点都是一个一个标着数字的球,每个球之间都使用线连着,并且他们都放在桌子上;不,挂在墙上是做好的,既保证了竖直,又保证了不会像地球仪一样绕着某个柱子转;因为当你把这个东西想象成立体的时候,就容易引起误会!一定要把它们放在二维平面上!为了使树恢复平衡,稍微有点经验的都会像下面展示的那么做,至于问为什么会这么做,只能说是直觉:
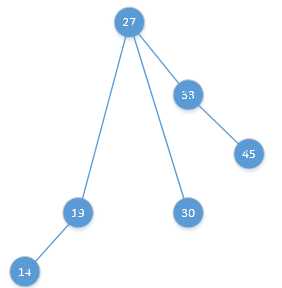
将27那个球竖直的向上拎起来,然后27 - 19、27 - 30的两根线会受力,也会向上移动,如下:
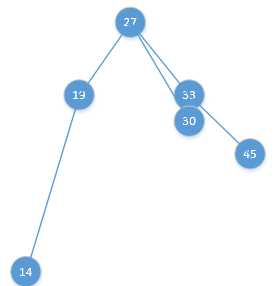
当30的那个球渐渐靠近33那个球的时候,会发生碰撞,30的球被33捕获,然后反弹,变成如下图所示的样子:
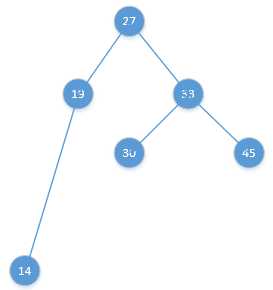
总结一下,这套东西的渐变图:




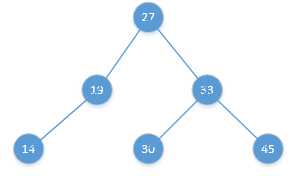
发现,这样变换之后确实既没有破坏二叉树的建立原则,有恢复了平衡。
2,RR型
即某个节点的右节点的右节点上再挂上一个节点,使树失去平衡,如下图:
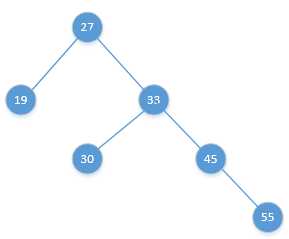
为了恢复二叉树的平衡,我们只要把33这个节点拎起来即可,渐变图如下:

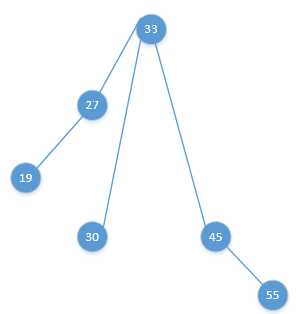
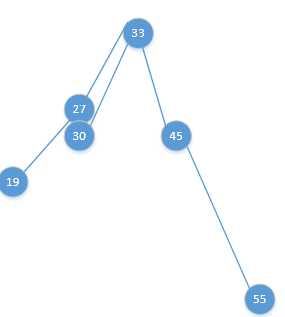
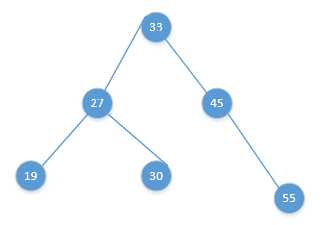
3,LR型
即某个节点的左节点的右节点上再挂上一个节点(这里不像上面RR型和LL型,这里挂上的节点在左边和在右边不一样,所以下面示意图就左右各挂一个),使树失去平衡,如下图:
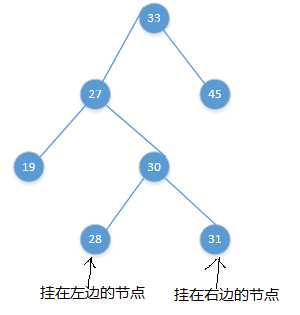
这种情况,我们要把30的那个球向27、33的两个球之间拎起来才行:
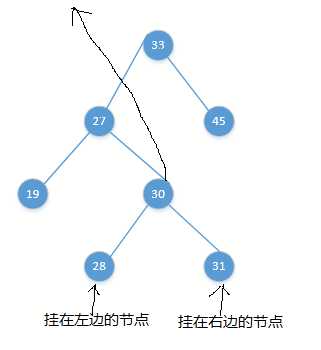
渐变图如下:
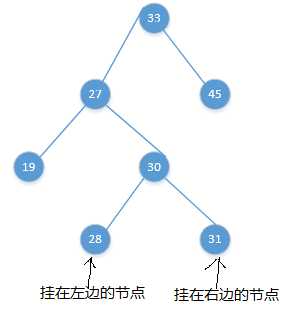

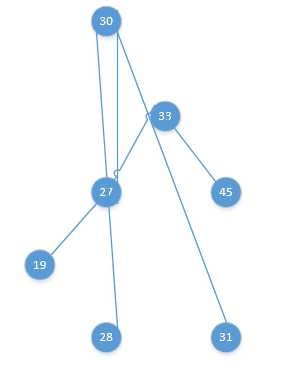
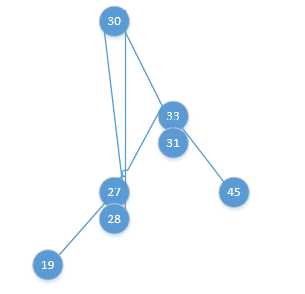
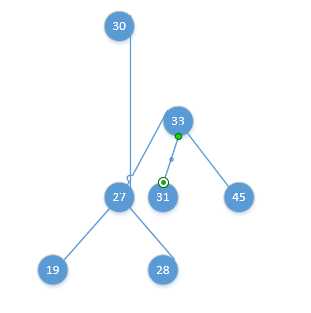
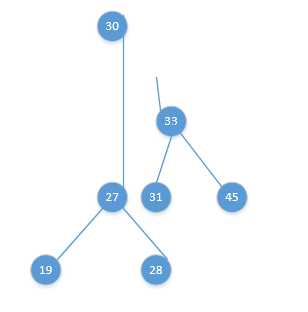
这里面还涉及到一个“力学变化”,就是,30从27 - 33之间穿过时,27 - 33之间的力会被破坏,也就是27 - 33之间的绳子会断裂,至于为什么是27的那头断裂,33的那头重新连接上30,恐怕是因为如果是相反的情况,就不成为一棵树了,所以导演编剧和上帝都不允许这样的情况发生。
4,RL型
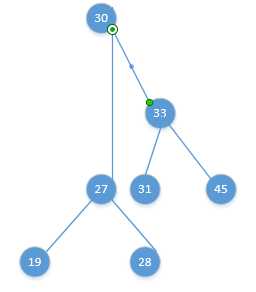
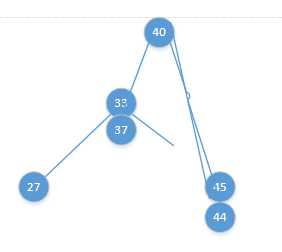
即某个节点的右节点的左节点上再挂上一个节点(这里不像RR型和LL型,这里挂上的节点在左边和在右边不一样,所以下面示意图就左右各挂一个),使树失去平衡,如下图:
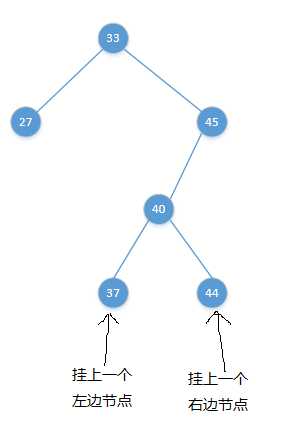
这种情况,我们要把40的球向 33 - 45 之间拎起来才行:
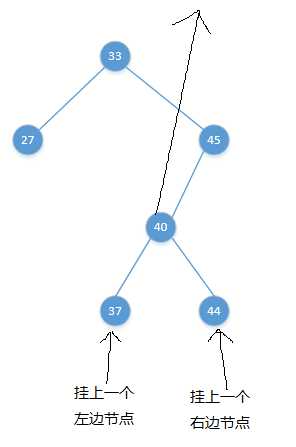
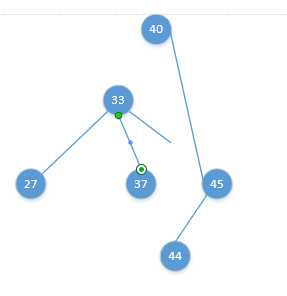
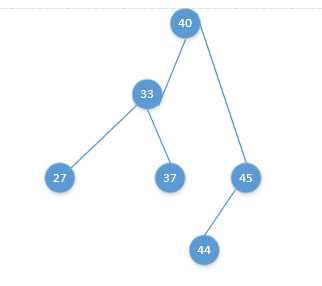
渐变图如下:


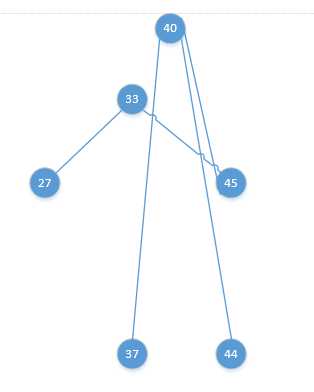
三、总结
1,树的旋转听起来容易产生误解,因为旋转既有可能在一个平面上旋转,也可能在一个三维中旋转(像地球仪绕着柱子转一样),还涉及到顺时针、逆时针...像我这样脑子不灵活的人不适合记忆这方面的概念;所以使用上面的方式去理解这个概念,可能是比较合适的;
2,大家一定会纳闷,为什么这么搞就能使树平衡?你把它想象成那种我们高中初中学过的证明题(因为啥啥啥,又因为啥啥啥,所以啥啥啥)那样证明这个东西就行了,看着纳闷,证明出来会发现是真的,因为颠来倒去就6个节点。这种感觉就像做证明题一样,你自己最后证明出来了,再回想一下还是觉得我为什么不能一看就明白,非要写下来证明才行....
3,我写上面的内容都是用visio画的,你把一个球拎起来的时候,球与球之间的连接线也会跟着拉长,很适合理解“拎起来”这个动作。
标签:问题 查找 并且 inf 地球仪 hashmap 记忆 说明 ash
原文地址:https://www.cnblogs.com/seeall/p/13259785.html