标签:als 矩阵 元素 ural 比较 haar 特征 需要 show
小波,就是很小的波,它的积分总是接近于 0;
小波 又分为 小波分解 和 小波包分解;
小波分解 只对 低频部分 进行分解,对高频部分不再分解,所以能够过滤掉 高频部分;
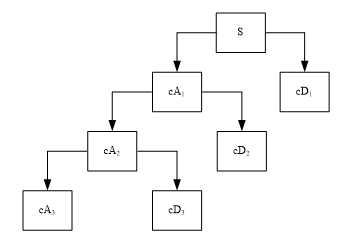
低频部分 代表了 趋势,也叫 近似信号;高频部分 代表了 噪声,也叫 细节信号;
小波包分解 则既对 低频部分 进行分解,也对 高频部分 进行分解;
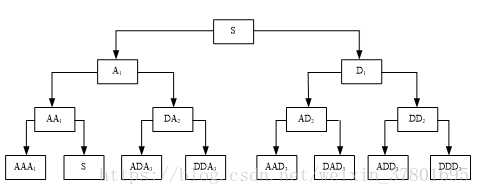
小波变换 就是把 一个波形 分解成 N个 低频部分 和 M个 高频部分 的 和;
同一个小波基函数可以通过 平移和缩放 生成不同的小波基;
小波变换就是 把 原始信号 与 小波基函数 以及 尺度函数 进行内积运算,所以一个 小波基 和一个 尺度函数 就确定了一个小波变换;
类比理解:小波基 就相当于 一个 标准正交基;原始信号 与 小波基 作内积 相当于 向量在 标准正交基上做投影;
CWT:连续的小波变换
DWT:离散的小波变换
安装
pip install PyWavelets
查看所有小波族
import pywt print(pywt.families()) # 查看所有小波基 # [‘haar‘, ‘db‘, ‘sym‘, ‘coif‘, ‘bior‘, ‘rbio‘, ‘dmey‘, ‘gaus‘, ‘mexh‘, ‘morl‘, ‘cgau‘, ‘shan‘, ‘fbsp‘, ‘cmor‘] print(pywt.families(short=False)) # [‘Haar‘, ‘Daubechies‘, ‘Symlets‘, ‘Coiflets‘, ‘Biorthogonal‘, ‘Reverse biorthogonal‘, ‘Discrete Meyer (FIR Approximation)‘, ‘Gaussian‘, ‘Mexican hat wavelet‘, ‘Morlet wavelet‘, ‘Complex Gaussian wavelets‘, ‘Shannon wavelets‘, ‘Frequency B-Spline wavelets‘, ‘Complex Morlet wavelets‘]
1D 多阶小波变换 wavedec
def wavedec(data, wavelet, mode=‘symmetric‘, level=None, axis=-1): """ Multilevel 1D Discrete Wavelet Transform of data. wavelet : Wavelet object or name string 小波基 Wavelet to use mode : str, optional 默认是对称的 Signal extension mode, see :ref:`Modes <ref-modes>`. level : int, optional Decomposition level (must be >= 0). If level is None (default) then it will be calculated using the ``dwt_max_level`` function. axis: int, optional Axis over which to compute the DWT. If not given, the last axis is used. Returns ------- [cA_n, cD_n, cD_n-1, ..., cD2, cD1] : list
level 指定了 分解 阶数
返回的是 各层的小波系数 【也就是 特征值,一个 信号 分解为 多个 波形,每个 波形 对应一个 小波系数,计算 这个小波系数 的范数,就是这个 波形 对应的 能量】
示例
import numpy as np from pywt import wavedec import matplotlib.pylab as plt np.random.seed(10) data = np.random.random((100, )) coeffs = wavedec(data, ‘db1‘, level=2) # 一维离散信号的小波变换 cA2, cD2, cD1 = coeffs # 一个低频,多个高频,高频数 取决于 level plt.subplot(411); plt.title(‘original‘); plt.plot(data) plt.subplot(412); plt.title(‘ca2‘); plt.plot(cA2) plt.subplot(413); plt.title(‘cd2‘); plt.plot(cD2) plt.subplot(414); plt.title(‘cd1‘); plt.plot(cD1) plt.show()
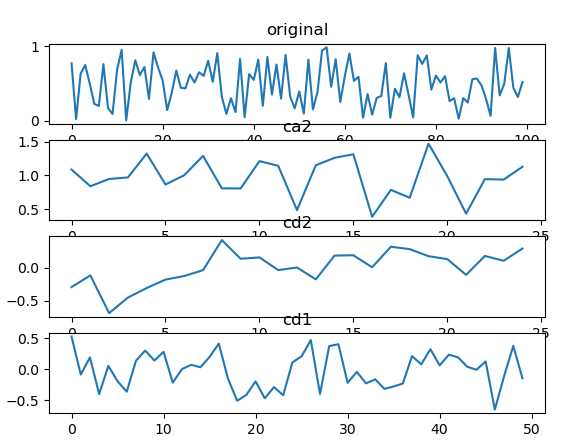
1D 1 阶小波分解
level = 2 相当于 进行了 2 次 1阶小波分解
def dwt(data, wavelet, mode=‘symmetric‘, axis=-1)
可以看到 没有 level 参数,level 恒为 1
与 wavedec 进行比对,指定 wavedec level=2,结果相同
np.random.seed(10) data = np.random.random((10, )) coeffs = wavedec(data, ‘db1‘, level=2) # 一维离散信号的小波变换 cA2, cD2, cD1 = coeffs # 一个低频,多个高频,高频数 取决于 level print(cA2) # [1.08726236 0.84094862 0.25745065] print(cD2) # [-0.29518976 -0.11764496 0. ] print(cD1) # [ 0.53073221 -0.08142734 0.19354246 -0.39772483 0.05711374] ### 一次 小波分解, level=1 a = data ca = [] # 近似分量 cd = [] # 细节分量 for i in range(2): (a, d) = pywt.dwt(a, ‘db1‘) # 进行2阶离散小波变换 ca.append(a) cd.append(d) print(ca) # [array([0.5600799 , 0.97754127, 0.51145292, 0.67782802, 0.1820451 ]), array([1.08726236, 0.84094862, 0.25745065])] ### 取最后一个 近似信号 print(cd) # [array([ 0.53073221, -0.08142734, 0.19354246, -0.39772483, 0.05711374]), array([-0.29518976, -0.11764496, 0. ])]
wavedec 相当于 dwt 的封装
用法 基本 等同于 1D
2D 1阶小波变换 dwt2
def dwt2(data, wavelet, mode=‘symmetric‘, axes=(-2, -1)): returns (cA, (cH, cV, cD)) : tuple
要注意返回值,分别为低频分量,水平高频、垂直高频、对角线高频。高频的值包含在一个tuple中
示例
import pywt import pywt.data # Load image original = pywt.data.camera() # Wavelet transform of image, and plot approximation and details titles = [‘Approximation‘, ‘Horizontal detail‘, ‘Vertical detail‘, ‘Diagonal detail‘] coeffs2 = pywt.dwt2(original, ‘bior1.3‘) # 2D 离散信号 小波分解 LL, (LH, HL, HH) = coeffs2 fig = plt.figure(figsize=(12, 3)) for i, a in enumerate([LL, LH, HL, HH]): ax = fig.add_subplot(1, 4, i + 1) ax.imshow(a, interpolation="nearest", cmap=plt.cm.gray) ax.set_title(titles[i], fontsize=10) ax.set_xticks([]) ax.set_yticks([]) fig.tight_layout() plt.show()
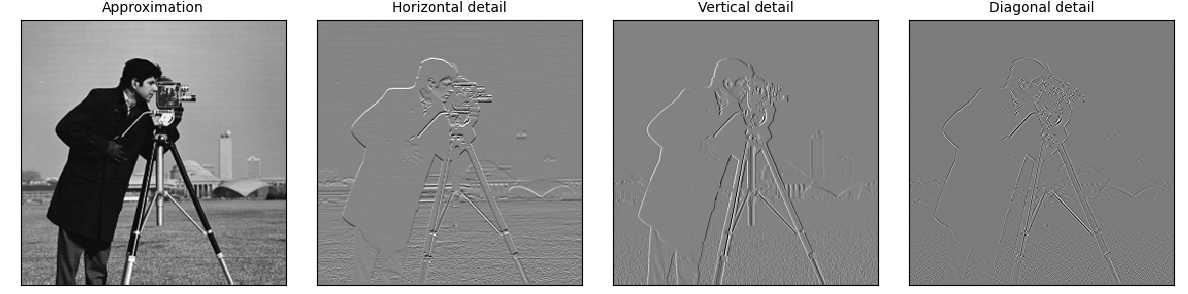
2D 多阶小波变换 wavedec2
print(pywt.waverec2(coeffs, wavelet=‘db1‘, level=3))
官网有 level 参数,我的版本没有,应该是版本问题,暂未解决
小波 经常用于 降噪,降完噪后 需要把 信号进行重构,生成无噪声的信号,1D、2D 用法类似
def waverec(coeffs, wavelet, mode=‘symmetric‘, axis=-1)
示例
import numpy as np import pywt import matplotlib.pylab as plt plt.rcParams[‘font.sans-serif‘]=[‘SimHei‘] plt.rcParams[‘axes.unicode_minus‘]=False data = np.hstack([np.ones((1, 10)), np.ones((1, 50)) * 2])[0] ca, cd2, cd1 = pywt.wavedec(data, ‘db1‘, level=2) plt.subplot(211) plt.title(‘original‘) plt.plot(data) out = pywt.waverec([ca, cd2, cd1], ‘db1‘) plt.subplot(212) plt.title(‘重构信号‘) plt.plot(out) plt.show()
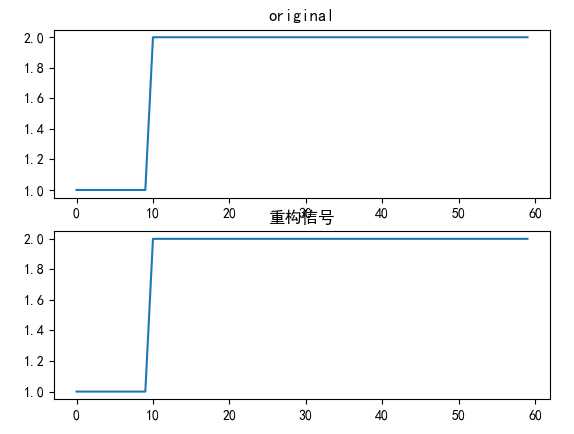
小波变换还是比较复杂的,确切地说 如果想 彻底弄懂,基本不可能,我这里 只重点记录下 学习心得
1. 傅里叶变换 的 基 只能是 正弦波,如果 原始波形 比较陡峭,需要无穷多的 正弦波 才能逼近 这种陡峭,计算量很大;小波基 则 比较 灵活,甚至可以自定义小波基;
2. 正弦波 会以 同样的 幅度 在无穷大空间内做 无限震动,能量巨大;而 小波 是一个 很短的波,它的能力比较集中,而且集中在 某一点附近; 如下图

之所以叫 小波,就是 跟 傅里叶的正弦波 比较起来 很小
3. 小波 擅长 瞬时突变 信号的检测,傅里叶变换无能为力

代码
#进行小波变换,提取样本特征 wp = pywt.WaveletPacket(SingleSampleDataWavelet, wavelet=‘db3‘, mode=‘symmetric‘, maxlevel=3) #小波包三层分解 #print([node.path for node in wp.get_level(3, ‘natural‘)]) #第3层有8个 #获取第level层的节点系数 aaa = wp[‘aaa‘].data #第1个节点 aad = wp[‘aad‘].data #第2个节点 ada = wp[‘ada‘].data #第3个节点 add = wp[‘add‘].data #第4个节点 daa = wp[‘daa‘].data #第5个节点 dad = wp[‘dad‘].data #第6个节点 dda = wp[‘dda‘].data #第7个节点 ddd = wp[‘ddd‘].data #第8个节点 #求取节点的范数 ret1 = np.linalg.norm(aaa,ord=None) #第一个节点系数求得的范数/ 矩阵元素平方和开方 ret2 = np.linalg.norm(aad,ord=None) ret3 = np.linalg.norm(ada,ord=None) ret4 = np.linalg.norm(add,ord=None) ret5 = np.linalg.norm(daa,ord=None) ret6 = np.linalg.norm(dad,ord=None) ret7 = np.linalg.norm(dda,ord=None) ret8 = np.linalg.norm(ddd,ord=None) #8个节点组合成特征向量 SingleSampleFeature = [ret1, ret2, ret3, ret4, ret5, ret6, ret7, ret8]
关键是 细节信号 的能量 计算,其实就是 系数(类似于特征值大小) 的 归一化
参考资料:
https://www.cnblogs.com/shuimuqingyang/p/10919918.html 小波变换库——Pywalvets 学习笔记
https://pywavelets.readthedocs.io/en/latest/ref/index.html PyWavelets 官网
https://github.com/PyWavelets/pywt PyWavelets git上的demo
https://blog.csdn.net/alwaystry/article/details/52756051 用法挺全的
https://zhuanlan.zhihu.com/p/44215123 小波变换完美通俗讲解系列之 (一) 【原理就看这篇吧】
https://blog.csdn.net/zds13257177985/article/details/102896041?utm_medium=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase 小波包变换/能量特征提取/结果图绘制-python代码
标签:als 矩阵 元素 ural 比较 haar 特征 需要 show
原文地址:https://www.cnblogs.com/yanshw/p/13253595.html