细菌觅食优化算法：理论基础，分析，以及应用(未完)

原作者：Swagatam Das,Arijit Biswas,Sambarta Dasgupta,和Ajith Abraham 

[摘 要]细菌觅食优化算法（Bacterial foraging optimization algorithm[BFOA]）已经被分布式优化和控制的同行们当作一种全局性的优化算法接受。BFOA是由大肠杆菌的群体觅食行为所启发而总结出来 的。BFOA已经吸引了足够多的研究者的注意，由于它出现在解决真实世界中一些应用领域上优化问题的高效性。E.coli 的群体策略的生物基础是用特别的方式和简单的优化算法来进行模仿。着一张以传统的通俗易懂的BFOA算法大纲开始。然后分析“根据这个简单的数学模型模拟 BFOA的趋向性步骤”的动态。从这个分析过程中找出线索，在运行过程中根据当前的细菌适应情况，调整趋向性步骤的参数大小，最终得出BFOA的适应性变 量。之后在BFOA中细菌复制操作中的动态数据分析将被讨论。这里将讨论BFOA技术与其他的优化技术的混合技术，还将提供一个大多数至今的重要的 BFOA应用的解释。

1介绍

细菌觅食优化算法(BFOA)，被Passino所提出，对于仿生学优化算法大家庭来说是一个新兴技术。对于过去的50年来，优化算法，像遗传算法（GA），进 化规划(EA),进化策略（ES），从进化和自然遗传上吸引了许多他们的灵感，已经占领了优化算法领域。最近自然群体激发了算法，像粒子群优化（PSO） 算法，蚁群算法（ACO）已经找到了它们通向领域并且高效性的路。紧接着相同的群体算法趋势，Passino在提出了BFOA算法。大肠杆菌群体觅食策略的应用在多元函数最优化算法中是一个很关键的想法原型。细菌以一种可以最大限度的提高单位时间内获得能量的方式去寻找食物。个体细菌通过发送信号来与其他的细菌进行交流。细菌在考虑前面两个因素之后做出进行觅食的决定。这个过程中，当寻找到食物后细菌做出最小的步长的移动，这个过程叫做趋化。BFOA的关键思想是在问题搜索空间模仿细菌趋化运动。

　　从该算法出现以来，BFOA吸引了许多来自不同知识领域的研究人员的关注，主要是由于它的生物学驱动方式和神奇优美的结构。研究人员正在尝试着去混合BFOA算法与其他不同的算法，尽量去探索该算法的局部和全局两个方面的特性。它已经被应用到许多现实世界的真实问题上，证明其他GA和PSO等多变量方面的高效性。数学模型，适应性，算法的修改可能是BFOA将来的主要研究方向。

　　本文的结构如下：第二部份提供BFOA算法的生物动力模型，并且全面的概括该算法。第三部份在传统的梯度下降搜索算法框架下提供一个关于趋化计算的简单数学分析。第四部份讲解了复制操作的数学模型。第五部分对BFOA算法与其他软计算算法的混合进行了探讨。第六部分提供了BFOA算法在不同的科学和能源领域的应用概述。第七部分进行了一个总结。

2细菌觅食优化算法

　　在实际的细菌觅食过程中，运动是靠一系列拉伸的鞭毛来实现的。鞭毛帮助的大肠杆菌细菌翻滚或游泳，这是由细菌在觅食时执行两个基本操作[7，8]。当它们顺时针方向翻转时，每一根鞭毛都会拉动细胞。这导致了鞭毛的独立运动，并且最终以最少的代价去翻转。然而，在糟糕的地方则频繁地翻转，去寻找一种营养梯度。逆时针方向移动鞭毛有助于细菌以非常快的速度游泳。在上面提到的算法中，细菌经历了趋化，朝着它们喜欢的营养梯度地方移动并且避免进入有害的环境。通常情况下，细菌在友好的环境中会移动较长的一段距离。图一描述了在营养问题上细菌是如何顺势转逆时针移动的。

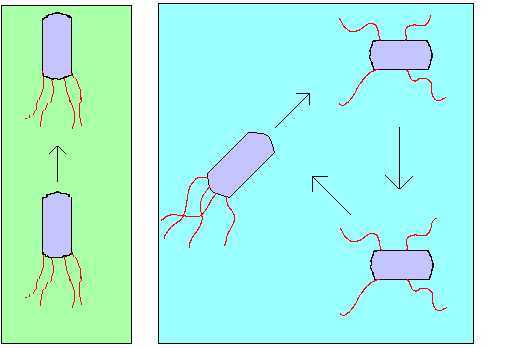
Fig.1. Swim and tumble of a bacterium

当它们获得了足够的食物，它们的长度增加以及面对着合适的温度，它们将从自己本身的中间断裂开来，形成两个新的细菌。这个现象启发Passino在BFOA中引进繁殖的事件。由于突然的环境变化或攻击发生后，趋化过程可能被破坏和一群细菌可能会转移到其他地方或者一些细菌可能被引进到细菌群中。这些构成了真实细菌环境中的消除-分散事件。一个区域内的所有细菌被杀死或者一组细菌分散到环境的新部分。

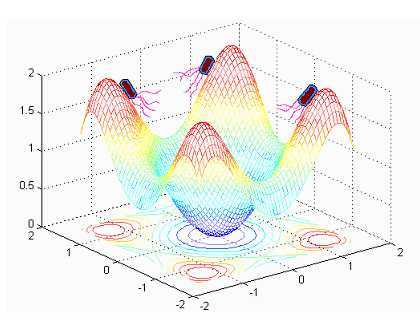
　　现在假设我们想要找到最小的J（θ），其中θ ∈ R (i.e. θ is a p-dimensional vector of real numbers)，并且我们没有关于梯度?J ( θ )的测量或者分析描述。BFOA模拟真是细菌系统中的这四个观察到的主要机制：趋化，群体，复制以及消除-分散。解决这个无梯度优化问题。一个虚拟细菌事实上是一个
实验方案（可能称为搜索代理）在其功能面移动（见Figure2)来寻找全局最优解。

 让我们定义一个翻转趋化步骤其次一次翻转或者运行后翻转。
让j作为趋化步骤索引。k作为复制步骤索引。l作为消除-分散步骤索引。同时让：
p:搜索空间维度
S:群体中细菌的总数
Nc:趋化步骤的步数
Ns:游泳长度
Nre:复制步骤的次数
Ned:消除-分散事件的次数
Ped:消除-分散概率
P( j , k , l ) = {θ ( j , k , l ) | i = 1,2,..., S}  
代表j-th趋化步骤中，S细菌群体中的每一个成员的位置，k-th复制步骤，l-th消除-分散事件。
J（i,j,k,l）
表示在i-th细菌 θ<i> ( j , k , l ) ∈ R p (sometimes we drop the indices and refer to the i-th bacterium position as θ i )搜索定位中的消耗（代价）。注意：我们将