标签:com 开始 方差 就是 稳定性 训练 最优 image 离散
打靶场上来了4个枪手,开始打靶,PIAPIAPIA……一阵枪响,不一会儿,打靶成绩出来了。以下是4位抢手的打靶结果:
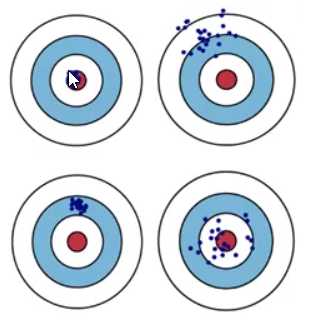
不难看出,第一位抢手打的又准,而且稳定性也好,把把命中红星。第二位枪手惨不忍睹,打的又偏,而且又毫无章法。第三位抢手准度一般,好在稳定性还不错,只要提升下准度,还是可以抢救一下。第四名枪手,稳定性不行,但是准度尚可,基本还是落在红星的附近。
看完打靶,我们现在再回头看看方差和偏差的数学解释:
偏差:描述的是预测值(估计值)的期望与真实值之间的差距。偏差越大,越偏离真实数据。
方差:描述的是预测值的变化范围,离散程度,也就是离其期望值的距离。方差越大,数据的分布越分散。
我们追求的是第一位枪手的结果:低偏差和低方差,也就是射的既准而且又稳定。我们讨厌的是第二位枪手的状态,射的不准,而且稳定性也不佳。
偏差和方差,用我们刚刚打靶的例子来说,一个就是准度,一个就是稳定性了。是我们拿到的已有数据,通过模型训练后,根据真实值和评估值,判断训练结果的一个方式。
那么,我们拿到数据训练后,有办法达到低方差和低偏差的状态呢?事实的情况往往是:鱼和熊掌,没法兼得,偏差和方差就像是跷跷板的两个头,按下葫芦浮起瓢,很尴尬。
对,这确实非常遗憾。很多情况就是如此,其最根本的原因就是:我们手头上有的,只可能是有限的数据,我们试图通过对有限的数据,来估计无限的真实样本空间。不得不说,这和盲人摸象没什么两样(原谅我再次用这个比喻,我也是黔驴技穷了)。

那么,我们还是用盲人摸大象的例子来说明问题吧:
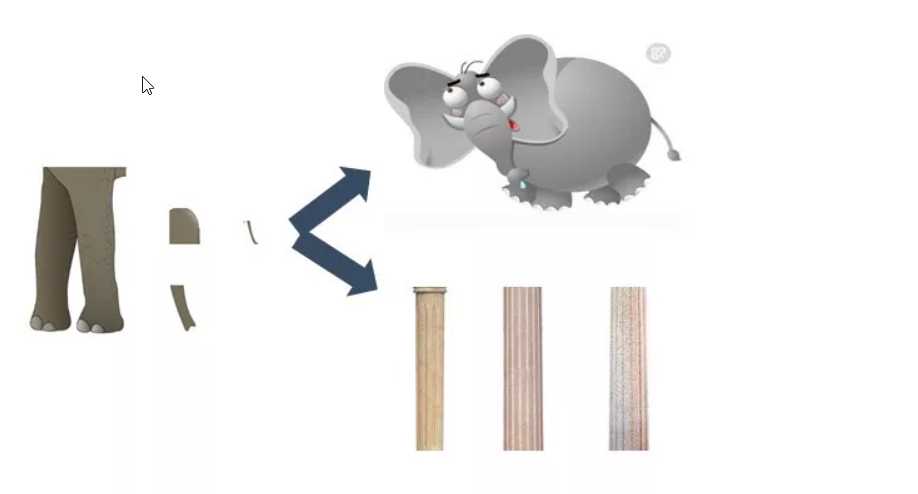
假设,大象是数据所有的样本空间分布,那么现实情况,我们拿到的数据往往是不全的,可能只是大象身体的一部分,比如说:2条腿,一部分的耳朵,一部分的尾巴,一部分的 鼻子等等。
对,就是如下图所示的玩意(PIA,这什么破玩意啊,狠狠的把这个破数据给砸了)

但是,即便只是2条腿,部分耳朵,尾巴和鼻子的图,我想在座的各位,一定也能一瞬间就能辨认出,这就是大象。这主要得益于各位对于大象的先验知识。但是我们的模型却没有在座的各位这么吊!
如果只考虑给予数据的真实性,而不去考虑先验知识,而只考虑去降低偏差的话,模型就会失去泛化能力,也就是我们常说的过拟合,这降低了模型在真实数据中的表现。模型会觉得,这个玩意是一个柱子,而不是大象。当然就提供的数据来看,确实更像是柱子,不对吗?但这实在是太糟糕了。相反的,如果我们充分相信自己的先验知识,在识别加入更多的限制,这显然会增加模型的偏差(因为给的数据和大象确实差远了)。但是识别的稳定性却提高了,如果给的数据中是1条腿,部分象牙、鼻子等数据,模型也能识别出这是一只大象。所以,如刚才所说的,偏差和方差是跷跷板的2头,很多时候只能去取2者之间的最优。
标签:com 开始 方差 就是 稳定性 训练 最优 image 离散
原文地址:https://www.cnblogs.com/654321cc/p/13264317.html