标签:node void 分解 大数 范围 大于 printf 国家 file

好像全机房除了我以外都精通 \(\rm NTT\) ,\(\rm QAQ\)
\(\rm FFT\):快速傅里叶变换,是用来做多项式乘法或者加法卷积以及其他运算的一种 \(\mathcal O(n \log n)\) 的方法
\(\rm FNTT及NTT\):快速傅里叶变换的优化版——快速数论变换—>优化常数及误差
\(\rm FWT\):快速沃尔什变换—>利用类似FFT的东西解决一类卷积问题
\(\rm MTT\):毛爷爷的FFT—>任意模数
\(\rm FMT\):快速莫比乌斯变化-> 可被暴力替代
参考资料:
https://www.cnblogs.com/Sakits/p/8416918.html
https://www.luogu.com.cn/blog/Soulist/duo-xiang-shi-quan-jia-tong
https://www.luogu.com.cn/blog/tbr-blog/duo-xiang-shi-xue-xi-bi-ji
https://www.cnblogs.com/cjoieryl/p/10114614.html
https://www.cnblogs.com/wxq1229/p/12235793.html
\(\qquad\rm FFT\) 虽然很棒,但是很显然用的 \(double\) 会有精度误差,所以我们试一试可不可以找一个正整数啥的来代替单位根——原根。
\(\qquad (1)\) 阶:对于 \(a \bot m\) ,满足 \(a^k\equiv 1\pmod m\) 的最小正整数 \(k\) 称为 \(a\) 对模 \(m\) 的阶,记作 \(\delta_m(a)\) 。
\(\qquad (2)\) 原根的定义: \(\delta_m(a)=\varphi(m)\) 的 \(a\) 称为模 \(m\) 的一个原根。(只有 \(2,4,p_x,2*p_x\) 才有原根,其中 \(p\) 是奇素数, \(x\) 是正整数。)
\(\qquad (3)\) 原根的求法: \(P\) 是一个质数。对于 \(P-1\) 质因数分解得 \(p_1^{a_1}\cdot p_2^{a_2} \cdots p_k^{a_k}\) ,枚举 \(g \in [1,P]\) ,若 \(g\) 满足 \(\forall i,g^{\frac{P-1}{p_i}} \not\equiv 1(\pmod P)\) ,则 \(g\) 是模 \(P\) 得原根。
\(\qquad (4)\) 原根的性质
\(\qquad\qquad\) 证明原根有单位根需要的性质,因此证明原根可以替代单位根代入求点值。
\(\qquad\qquad\) 设 \(g_{n}^{1}=g^{\frac{P-1}{n}}\) ,这样就也可以向单位根那样放到一个圆上去看。
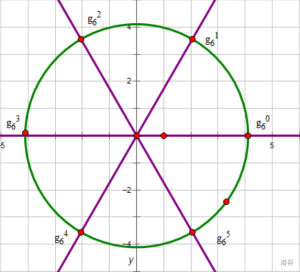
\(\qquad\quad ①\) 对于 \(n\) 次原根 \(g\) ,有 \(g^k(0\le k < P)\) 在 \(\pmod P\) 下互不相等。
\(\qquad\qquad\)证:若 \(g^k \equiv g_j\) 且 \(k>g\) ,则有 \(g^{k-j} \equiv 1\) ,但是 \(k-j < \varphi(P)\) ,则 \(\varphi(P)\) 不是最小的阶,也就不是原根,与定义矛盾,得证。
\(\qquad\quad ②\) \(g_{n}^{2k}=g_{n/2}^{k}\)
\(\qquad\qquad\) 证:\(g_{n}^{2k}=g^{\frac{P-1}{n}\times 2k}=g^{\frac{P-1}{n/2}\times k}=g_{n/2}^{k}\) ,得证。或者放到图上去证明也是可以的。
\(\qquad\quad ③\) \(g_n^{k+n/2}=-g_n^{k}\)
\(\qquad\qquad\) 证:丢圆上。
\(\qquad\quad ④\) \(\sum_{j=0}^{n-1}(g_n^k)^j=n\times [k==0]\)
\(\qquad\qquad\) 证:等比数列求和
\(\qquad\qquad\) 和 \(\rm FFT\) 大致相同,代码如下:
#define int ll
il ll kpow(ll x,ll k){
ll ans=1,now=x;
while(k){
if(k&1)ans=1ll*ans*now%P;
now=1ll*now*now%P;k>>=1;
}return ans;
}
il void NTT(ll *x,int f,int len){
if(len==1)return;
ll f1[len>>1],f2[len>>1];
for(int i=0;i<len;i+=2)f1[i/2]=x[i],f2[i/2]=x[i+1];
NTT(f1,f,len>>1),NTT(f2,f,len>>1);
ll G=1,bas=kpow(3,(P-1)/(len));
if(f==-1)bas=kpow(bas,P-2);
rep(i,0,(len>>1)-1){
x[i]=(f1[i]+1ll*G*f2[i]%P)%P;
x[i+(len>>1)]=(f1[i]-1ll*G*f2[i]%P+P)%P;
G=1ll*G*bas%P;
}return;
}
signed main(){
n=read();m=read();
rep(i,0,n)a[i]=(read()+P)%P;
rep(i,0,m)b[i]=(read()+P)%P;
while((1<<lim)<=n+m)++lim;
NTT(a,1,(1<<lim));NTT(b,1,(1<<lim));
rep(i,0,(1<<lim))a[i]=1ll*a[i]*b[i]%P;
NTT(a,-1,(1<<lim));int inv=kpow((1<<lim),P-2);
rep(i,0,n+m)printf("%lld ",a[i]*inv%P);puts("");
return 0;
}
\(\qquad\qquad\) 注意,当 \(f=\rm -1\) 时,并不是 \(\rm bas=-bas\) 。因为原根中 \(g_n^{-i}=inv[g_n^i]\ne-g_n^i\)
\(\qquad\qquad\) 这是递归版的写法,不卡一下常板子题会 \(T\) 一个点,于是我们来谈谈迭代版。
\(\qquad\qquad\)我们具体地观察一下 \(\rm NTT,FFT\) 的递归过程,它是类似一个树结构的:
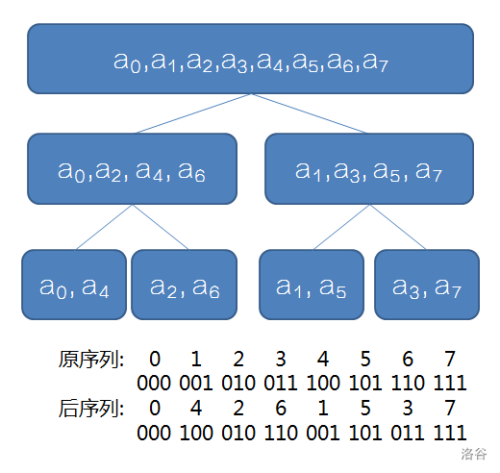
\(\qquad\qquad\)于是我们可以发现我们递归的序列的每一位其实原序列的二进制数反过来,这要怎么求呢?
while(lim<=n+m)lim<<=1,l++;
for(int i=0;i<lim;++i)r[i]=((r[i>>1]>>1)|((i&1)<<(l-1)));
\(\qquad\qquad\)显然本来 \(i=(\frac{i}{2}<<1)\) ,那么反过来就是 \(i=(\frac{i}{2}>>1)\) ,再额外处理一下奇数就可以了。这样我们求出来的新的 \(a\) 就是已经是迭代序列了。
for(int i=0;i<lim;++i)if(i<r[i])swap(a[i],a[r[i]]);
for(int mid=1;mid<lim;mid<<=1){//mid是当前区间的长度的一半
node bas=(node){cos(2.0*pi/mid),f*sin(2.0*pi/mid)};
for(int R=mid<<1,j=0;j<lim;j+=R){//R是当前区间的长度,j是当前区间的最左端点
node w=(node){1,0};
for(int k=0;k<mid;++k){//k是当前区间枚举到的第k个数,然后只需要枚举左半边
double x=A[j+k],y=A[j+k+mid];
A[j+k]=x+w*y;
A[j+k+mid]=x-w*y;
}
}
}return;
\(\qquad\qquad\)\(\rm NTT\) 是这样的:
rep(i,0,lim-1)if(i<r[i])swap(A[i],A[r[i]]);
for(int mid=1;mid<lim;mid<<=1){
int bas=kpow(3,(P-1)/(mid<<1));
if(!f)bas=kpow(bas,P-2);
for(int R=mid<<1,j=0;j<lim;j+=R){
int g=1;
for(int k=0;k<mid;++k,g=1ll*g*bas%P){
int x=A[j+k],y=A[j+k+mid];
A[j+k]=(x+1ll*g*y%P)%P;
A[j+k+mid]=(x-1ll*g*y%P+P)%P;
}
}
}return;
\(\qquad\qquad\) 差不多理解一下然后背一下代码吧。
\(\qquad\) 由于 \(n=2^k\) 且 \(n|(P-1)\) ,则可用的 \(P\) 应等于 \(c \times 2^k +1\) ,同时 \(P\) 是质数。所以说 \(\rm NTT\) 对于模数的限制还是挺大的。常见的模数有 \(998244353,1004535809,469762049\) ,它们的原根都是 \(3\) 。也可以打表找一些。
\(\qquad\)那么对于任意模数的情况我们要怎么做呢?
\(\qquad\)有两种做法:多次 \(\rm NTT + CRT\) 和 \(MTT\)
\(\qquad (1)\) 多次 \(\rm NTT+CRT\)
\(\qquad\qquad\) 一般是用上面三种常用模数分别做三次 \(\rm NTT\) ,这样对于每一个系数 \(x\) 我们得到了三组同余方程:
\(\qquad\qquad\)然后用中国剩余定理解一下就可以了。代码自己写吧,如果您愿意的话 (反正我调到心态崩了)
\(\qquad\qquad\) 为什么要三个模数求三次呢?为什么两个不可以呢?这是因为对于每一位系数 \(f(k)=\sum_{i+j=k}A_i+B_j\) , \(\sum\)是 \(10^5\) 级的,\(A,B\) 是 \(10^9\) 级别,不取模时可以达到 \(10^{23}\) 的数量级!而 \(t\) 个同余方程求 \(CRT\) 后的最终结果是 \((mod~lcm(m_1,m_2\cdots m_t))\) 的,也就是说最大能达到 \(lcm(m_1,m_2\cdots m_t)\) 的数量级,由于 \(m\) 两两互质,也就是能达到 \(m_1m_2 \cdots m_t\) 的数量级。而 \(m=998244353\) 或 \(1004535809\) 之类的约是 \(10^9\) 数量级的数,如果只选两个模数,这两个同余方程能达到的最大数量级只有 \(10^{18}\) ,是不能表示所有没取模的数的,所以至少要用三个模数运算三次。
\(\qquad\qquad\)但是这样子要求 \(9\) 次 \(\rm DFT\) ,常数巨大,而且可能会爆 \(long~long\) 。于是有一点小技巧如下。
\(\qquad\qquad\)先合并前两个,其中 \(inv(a,b)\) 表示在模 \(b\) 意义下 \(a\) 的逆元,由①②求 \(CRT\) 得:
\(\qquad\qquad\)设 \(k\) 等于同余符号右边的那一串,则
\(\qquad\qquad\)同时:
\(\qquad\qquad\)则
\(\qquad\qquad\)由于 \(x < m_1m_2m_3\) ,故 \(t < m_3\) ,所以可以求出 \(t=(c-k)*inv(m_1 *m_2,m_3)\) ,也就可以求出 \(x\) ,再对题目给定的模数 \(P\) 取模即可。这样就可以避免爆 \(long~long\) 。
\(\qquad\qquad\)代码如下:
#define int ll
const int maxn=4e5+5,P[4]={0,469762049,998244353,1004535809},
int kpow(int x,int k,int mod){
int ans=1,now=x;
while(k){
if(k&1)ans=1ll*ans*now%mod;
now=1ll*now*now%mod;k>>=1;
}return ans;
}
int kmult(int a,int b,int mod){//防溢出
a%=mod,b%=mod;
return ((a*b-(int)((int)((long double)a/mod*b+1e-3)*mod))%mod+mod)%mod;
}
void NTT(int *A,int f,int mod){
rep(i,0,lim-1)if(i<r[i])swap(A[i],A[r[i]]);
for(int mid=1;mid<lim;mid<<=1){
int bas=kpow(3,(mod-1)/(mid<<1),mod);
if(!f)bas=kpow(bas,mod-2,mod);
for(int R=mid<<1,j=0;j<lim;j+=R){
int g=1;
for(int k=0;k<mid;++k,g=1ll*g*bas%mod){
int x=A[j+k],y=1ll*g*A[j+k+mid]%mod;
A[j+k]=(x+y)%mod;A[j+k+mid]=(x-y+mod)%mod;
}
}
}return;
}
signed main(){
//file(a);
n=read();m=read();p=read();int k,t,x,inv;
rep(i,0,n){x=read();rep(j,0,3)a[j][i]=x;}
rep(i,0,m){x=read();rep(j,0,3)b[j][i]=x;}
while(lim<=n+m)lim<<=1,++l;
rep(i,0,lim-1)r[i]=((r[i>>1]>>1)|((i&1)<<(l-1)));
rep(i,1,3){
NTT(a[i],1,P[i]),NTT(b[i],1,P[i]);
rep(j,0,lim-1)a[i][j]=1ll*a[i][j]*b[i][j]%P[i];
NTT(a[i],0,P[i]);
inv=kpow(lim,P[i]-2,P[i]);
rep(j,0,lim-1)a[i][j]=1ll*a[i][j]*inv%P[i];
//rep(j,0,n+m)cout<<a[i][j]<<" ";cout<<endl;
}int m1=P[1],m2=P[2],m3=P[3],mm=1ll*m1*m2;
rep(i,0,n+m){
int a1=a[1][i],a2=a[2][i],a3=a[3][i];
k=(kmult(1ll*a1*m2%mm,kpow(m2%m1,m1-2,m1),mm)+
kmult(1ll*a2*m1%mm,kpow(m1%m2,m2-2,m2),mm))%mm;
t=1ll*((a3-k)%m3+m3)%m3*kpow(mm%m3,m3-2,m3)%m3;
x=(1ll*(t%p)*(mm%p)%p+(k%p))%p;
printf("%lld ",x);
}
return 0;
}
\(\qquad\qquad\)当然常数大的问题还是没有解决。
\(\qquad(2)\) 拆系数 $ \rm FFT$
\(\qquad\qquad\)显然当值大于一定限度的时候 \(FFT\) 才会爆精度,于是我们想办法把每项系数控制一下范围。
\(\qquad\qquad\)设 \(M=\sqrt{P}\) ,多项式每一项的系数可以表示为 \(A \times M+B\) 且 \(A,B\) 都在 \(M\) 的范围内即为 \(10^5\) 级别,相对来说比较安全。那么两个多项式的点值相乘相当于 \((a_1*M+b_1) *(a_2 * M+b_2)\) 也就等于:
\(\qquad\qquad\)于是我们对于 \(A_1,A_2,B_1,B_2\) 分别 \(\rm DFT\) ,再将 \((a_1*a_2),(a_1 * b_2+a_2 * b_1),(b_1 * b_2)\) 分别做 \(\rm IDFT\) ,最后将答案合并,就可以得到最终结果。当然也可以再加一个 \(\rm long~double\) 以防万一。
const int maxn=4e5+5,M=32768,inf=0x3f3f3f3f;
void FFT(node *A,int f){
rep(i,0,lim-1)if(i<r[i])swap(A[i],A[r[i]]);
for(int mid=1;mid<lim;mid<<=1){
node bas=(node){cos(pi/mid),f*sin(pi/mid)};
for(int R=mid<<1,j=0;j<lim;j+=R){
node w=(node){1,0};
for(int k=0;k<mid;++k,w=w*bas){
node x=A[j+k],y=w*A[j+k+mid];
A[j+k]=x+y;A[j+k+mid]=x-y;
}
}
}return;
}
int get(ld x,int k){return ((int)(x/lim+0.5)%P*k%P);}
signed main(){
//file(a);
n=read();m=read();P=read();int x;
while(lim<=n+m)lim<<=1,++l;
rep(i,0,lim-1)r[i]=((r[i>>1]>>1)|((i&1)<<(l-1)));
rep(i,0,n)x=read(),a1[i].x=x/M,b1[i].x=x%M;
rep(i,0,m)x=read(),a2[i].x=x/M,b2[i].x=x%M;
FFT(a1,1),FFT(a2,1),FFT(b1,1),FFT(b2,1);
rep(i,0,lim-1){
ans[1][i]=a1[i]*a2[i];
ans[2][i]=a1[i]*b2[i]+a2[i]*b1[i];
ans[3][i]=b1[i]*b2[i];
}
FFT(ans[1],-1),FFT(ans[2],-1),FFT(ans[3],-1);
rep(i,0,n+m){
int k1=get(ans[1][i].x,M*M%P);
int k2=get(ans[2][i].x,M%P);
int k3=get(ans[3][i].x,1);
printf("%lld ",((k1+k2)%P+k3)%P);
}
return 0;
}
\(\qquad\qquad\) 实测比三次 \(\rm NTT+CRT\) 快了四倍 (也可能是我代码写太丑了)
\(\qquad(3) \rm MTT\)
\(\qquad\qquad\) \(\rm MTT\) 是优化后的拆系数 \(\rm FFT\) ,只需要求 \(4\) 次 \(\rm DFT\) 而且不会爆精度。但是一般情况下求 \(7\) 次也不会 \(T\) ,所以我就没有去学 \(\rm MTT\) 了,有兴趣可以自己去看一看别的博客。比如说 这个 还有 这个 。或者有一篇 \(2016\) 年国家集训队论文讲这个的,是毛爷爷写的 (其实这玩意儿就是毛爷爷搞的)
标签:node void 分解 大数 范围 大于 printf 国家 file
原文地址:https://www.cnblogs.com/Zikual/p/13276319.html