标签:一点 add range 缩小 tps idg mic 梯度下降 回归算法
import numpy as np import matplotlib.pyplot as plt def loadDataSet(filename): dataSet = np.loadtxt(filename) m,n = dataSet.shape data_X = dataSet[:,0:n-1] data_Y = dataSet[:,n-1] return data_X,data_Y
def standRegres(data_X,data_Y): XTX = data_X.T@data_X XT = data_X.T if np.linalg.det(XTX) == 0: #linalg.det用于求解方阵行列式,如果求解的行列式值=0,则不可以求逆 print("data X cann`t inverse") return W = np.linalg.inv(XTX)@XT@data_Y return W
data_X,data_Y = loadDataSet("ex0.txt") W = standRegres(data_X,data_Y) plt.figure() plt.scatter(data_X[:,1].flatten(),data_Y.flatten(),c="green",marker="o") x = np.linspace(0,1,100) print(W) y = W[0]+W[1]*x plt.plot(x,y) plt.show()
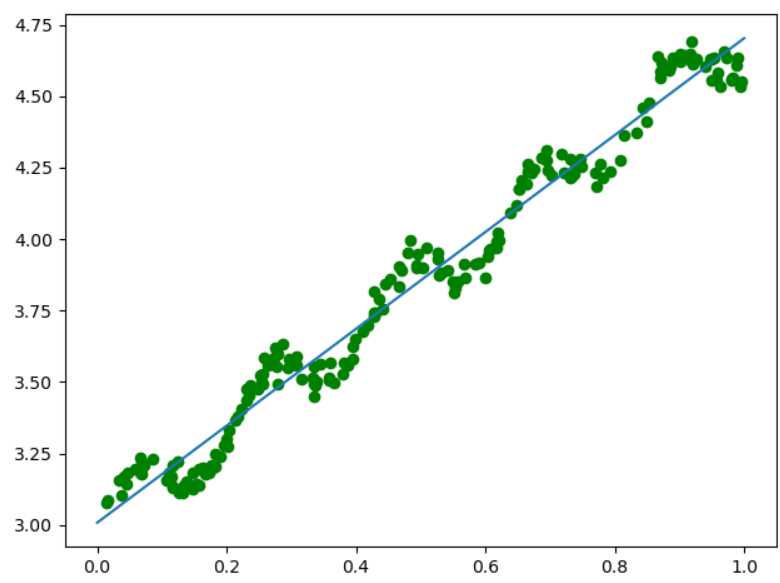
解释见机器学习实战。通过W矩阵的对角线上设置不同的数值,表示对不同的数据样本数值不同的权重(与支持向量机中的核类似)。
对于预测值距离标签值越近的点,我们设置的权重越大,越远设置越小。这里我们使用的是高斯核:其对应的权重如下:
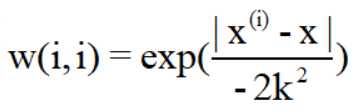
从公式中,我们可以看到k,即方差影响了高斯分布的收敛速度,当k越小时,下降速度越快,因此考虑的样本数(局部、附近)也就越少,故而对于当前局部样本数据点的拟合直线也就越符合当前的局部数据点(而非全局)。当我们迭代访问完成全部数据后,会发现拟合的模型为折线,而非直线,因为折线的每一段都是对局部样本集的最好拟合,而直线是对全局数据点的拟合。
所以当我们设置的k值越小,高斯收敛越快,涉及的局部样本点越少,折线段数越多,导致对全局样本的拟合程度超过我们预期的拟合模型,变为过拟合,所以合理的选取k值,是一个重要的问题。
import numpy as np import matplotlib.pyplot as plt def loadDataSet(filename): dataSet = np.loadtxt(filename) m,n = dataSet.shape data_X = dataSet[:,0:n-1] data_Y = dataSet[:,n-1] return data_X,data_Y
def lwlr(testPoint,data_X,data_Y,k=1.0): #求解当前样本点的权重W,从而获取当前样本点的预测值 m,n = data_X.shape W = np.eye(m) for i in range(m): #对每一个样本点都求解其权重 diff = testPoint - data_X[i,:] #样本点差距,是个向量,还要进行处理 W[i,i] = np.exp(diff@diff.T/(-2*k**2)) XTWX = data_X.T@W@data_X XT = data_X.T if np.linalg.det(XTWX) == 0: #linalg.det用于求解方阵行列式,如果求解的行列式值=0,则不可以求逆 print("data X cann`t inverse") return W = np.linalg.inv(XTWX)@XT@W@data_Y return testPoint@W.T #返回当前样本点的预测值
def lwlrTest(testPoint,data_X,data_Y,k=1.0): yPred = np.zeros(data_Y.shape) for i in range(data_X.shape[0]): yPred[i] = lwlr(testPoint[i], data_X, data_Y, k) return yPred
data_X,data_Y = loadDataSet("abalone.txt") yPred = lwlrTest(data_X,data_X,data_Y,1.0) #注意:因为绘制折线图是从左向右逐步绘制的,所以我们的数据需要进行排序处理,将data_X和yPred进行排序之后处理 SortIdx = data_X[:,1].argsort(0) #小到大排序,获取索引 Sort_X = data_X[SortIdx] plt.figure() plt.scatter(data_X[:,1].flatten(),data_Y.flatten(),c="green",marker="o") plt.plot(Sort_X[:,1].flatten(),yPred[SortIdx].flatten(),c="r") plt.show()
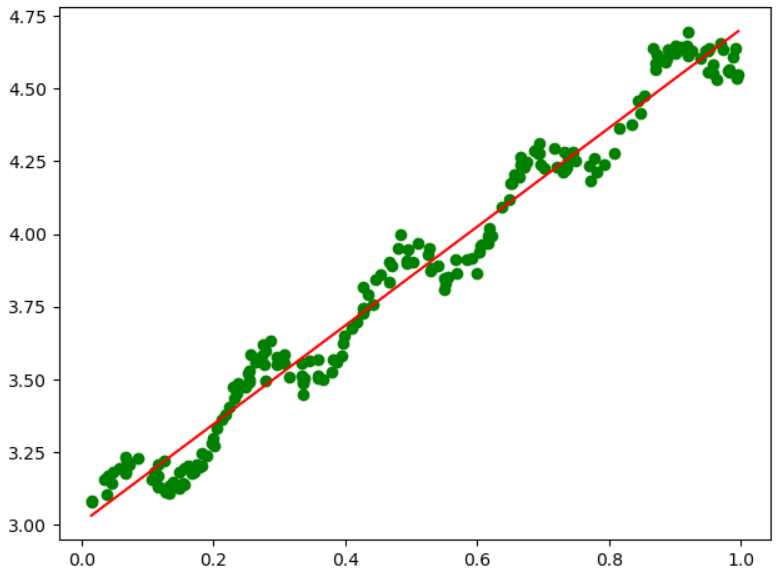
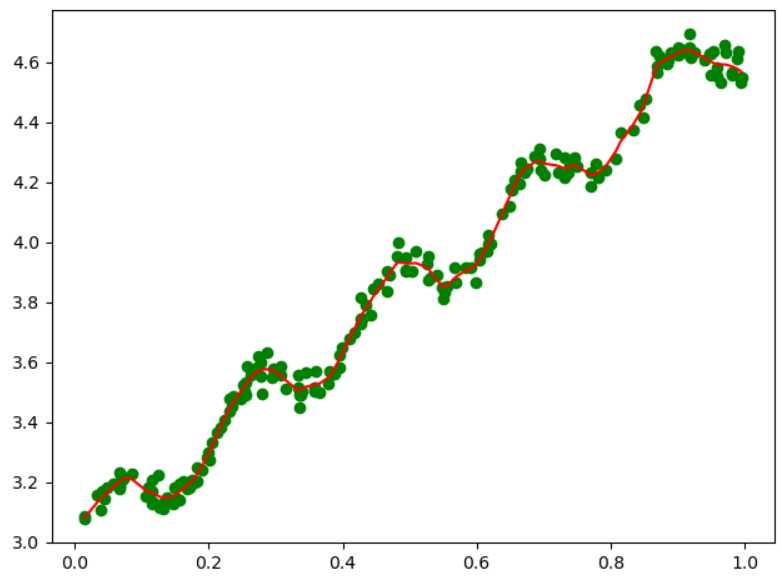
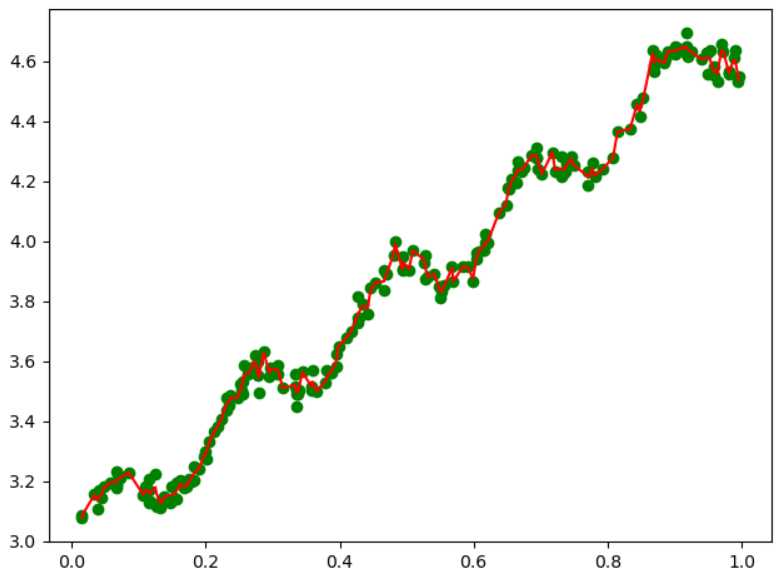
import numpy as np import matplotlib.pyplot as plt def loadDataSet(filename): dataSet = np.loadtxt(filename) m,n = dataSet.shape data_X = dataSet[:,0:n-1] data_Y = dataSet[:,n-1] return data_X,data_Y def lwlr(testPoint,data_X,data_Y,k=1.0): #求解当前样本点的权重W,从而获取当前样本点的预测值 m,n = data_X.shape W = np.eye(m) for i in range(m): #对每一个样本点都求解其权重 diff = testPoint - data_X[i,:] #样本点差距,是个向量,还要进行处理 W[i,i] = np.exp(diff@diff.T/(-2*k**2)) XTWX = data_X.T@W@data_X XT = data_X.T if np.linalg.det(XTWX) == 0: #linalg.det用于求解方阵行列式,如果求解的行列式值=0,则不可以求逆 print("data X cann`t inverse") return W = np.linalg.inv(XTWX)@XT@W@data_Y return testPoint@W.T #返回当前样本点的预测值 def lwlrTest(testPoint,data_X,data_Y,k=1.0): yPred = np.zeros(data_Y.shape) for i in range(data_X.shape[0]): yPred[i] = lwlr(testPoint[i], data_X, data_Y, k) return yPred
def rssError(yArr,yHatArr): return ((yArr-yHatArr)**2).sum()
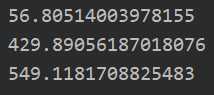
data_X,data_Y = loadDataSet("abalone.txt") yPred01 = lwlrTest(data_X[0:99],data_X[0:99],data_Y[0:99],0.1) print(rssError(data_Y[0:99],yPred01)) yPred1 = lwlrTest(data_X[0:99],data_X[0:99],data_Y[0:99],1) print(rssError(data_Y[0:99],yPred1)) yPred10 = lwlrTest(data_X[0:99],data_X[0:99],data_Y[0:99],10) print(rssError(data_Y[0:99],yPred10))
yPred01 = lwlrTest(data_X[100:199],data_X[0:99],data_Y[0:99],0.1) print(rssError(data_Y[100:199],yPred01)) yPred1 = lwlrTest(data_X[100:199],data_X[0:99],data_Y[0:99],1) print(rssError(data_Y[100:199],yPred1)) yPred10 = lwlrTest(data_X[100:199],data_X[0:99],data_Y[0:99],10) print(rssError(data_Y[100:199],yPred10))
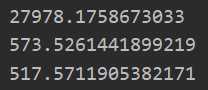
总感觉这样测试有问题....,因为实际中测试中还是使用了测试集数据去拟合数据
import numpy as np import matplotlib.pyplot as plt def loadDataSet(filename): dataSet = np.loadtxt(filename) m,n = dataSet.shape data_X = dataSet[:,0:n-1] data_Y = dataSet[:,n-1] return data_X,data_Y
def ridgeRegres(data_X,data_Y,lam=0.2): #计算回归系数 XTX = data_X.T@data_X new_dataX = XTX+np.eye(data_X.shape[1])*lam if np.linalg.det(new_dataX) == 0: print("can`t inverse") return W = np.linalg.inv(new_dataX)@data_X.T@data_Y return W
def ridgeTest(data_X,data_Y): #查看lamda选择值的表现 #数据归一化 newData_X = (data_X - np.mean(data_X,0))/np.var(data_X,0) newData_Y = data_Y - np.mean(data_Y,0) lamdaNums = 30 W = np.zeros((lamdaNums,newData_X.shape[1])) print(W.shape) for i in range(lamdaNums): Wi = ridgeRegres(newData_X,newData_Y,np.exp(i-10)) W[i] = Wi.T return W
data_X,data_Y = loadDataSet("abalone.txt") W = ridgeTest(data_X,data_Y) plt.figure() plt.plot(W) plt.show()
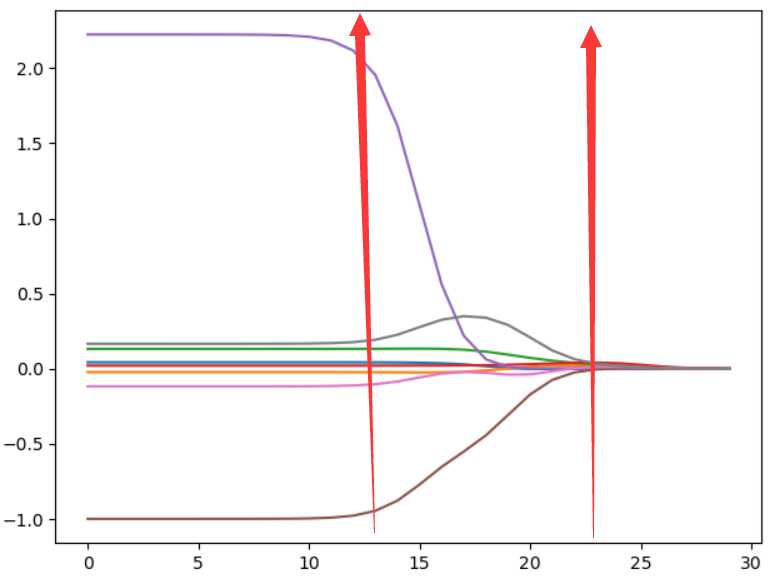
Ridge回归在不抛弃任何一个变量的情况下,缩小了回归系数,使得模型相对而言比较的稳定,但这会使得模型的变量特别多,模型解释性差。
有没有折中一点的办法呢?即又可以防止过拟合,同时克服Ridge回归模型变量多的缺点呢?有,这就是下面说的Lasso回归。

Lasso回归使得一些系数变小,甚至还是一些绝对值较小的系数直接变为0,因此特别适用于参数数目缩减与参数的选择,因而用来估计稀疏参数的线性模型。
但是Lasso回归有一个很大的问题,导致我们需要把它单独拎出来讲,就是它的损失函数不是连续可导的,由于L1范数用的是绝对值之和,导致损失函数有不可导的点。
也就是说,我们的最小二乘法,梯度下降法,牛顿法与拟牛顿法对它统统失效了。那我们怎么才能求有这个L1范数的损失函数极小值呢?
接下来介绍两种全新的求极值解法:坐标轴下降法(coordinate descent)和最小角回归法( Least Angle Regression, LARS)。
....
太烦了,以后用到再说(https://www.cnblogs.com/wmx24/p/9555219.html)
标签:一点 add range 缩小 tps idg mic 梯度下降 回归算法
原文地址:https://www.cnblogs.com/ssyfj/p/13275237.html