标签:实现 区别 a* star 覆盖 line info http include
题目:给你n个点,m条边的图,每个点有点权,有一些点是“酒吧”点,终点只能在“酒吧”,起点给定,路可以重复经过,但点权只能加一次,求最大的结果。
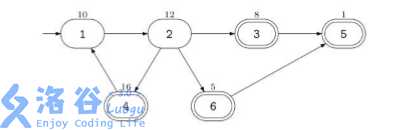
例如这个图,双实线表示是酒吧,结果呢是1->2->4->1->2->3->5所得值。
输入格式:
第一行N,M,下面M行是边,下面N行是点权,下面1行是起点与酒吧数量,下面一行是“酒吧”点的编号。
思路:
注意到:(边可以重复走,而点权只算一遍)这个条件,说明只要走到了一个环中的一个点,这个环里面所有点就一定都能走到,因为你可以走一圈回到入环的起点。
这是什么呢?这是名为“缩点”的高级技巧在呼唤!
我们可以把所有环看作一个点,权值是环内所有点权之和,只要环中有一个点是“酒吧”,那这个大环就可以看作一个“酒吧”,然后从起点所在“大点”开始,跑一遍单源最短路,找最大的路径长度即可(spfa最长路,dfs硬搜会被卡(搜,就硬搜))
代码:
#include<queue> #include<cstdio> #include<iostream> #include<cstring> #include<algorithm> using namespace std; const int maxn=5e5+10; struct E{int from,to,next;}edge[maxn]; E edge2[maxn];int head2[maxn],tot2; int head[maxn],tot; void add(int from,int to){ edge[++tot].from=from; edge[tot].to=to; edge[tot].next=head[from]; head[from]=tot; } void add2(int from,int to){ edge2[++tot2].to=to; edge2[tot2].next=head2[from]; head2[from]=tot2; } int dfn[maxn],vis[maxn],low[maxn]; int sta[maxn],top,Time; int belong[maxn],belongcnt,size[maxn]; int val[maxn],drink[maxn],drink2[maxn]; void tarjan(int u){ if(dfn[u])return; low[u]=dfn[u]=++Time; vis[u]=1;sta[++top]=u; for(int i=head[u];i;i=edge[i].next){ int v=edge[i].to; if(!dfn[v]){ tarjan(v); low[u]=min(low[u],low[v]); }else if(vis[v]){ low[u]=min(low[u],dfn[v]); } } if(low[u]==dfn[u]){ belongcnt++; while(sta[top+1]!=u){ belong[sta[top]]=belongcnt; size[belongcnt]+=val[sta[top]]; vis[sta[top]]=0; if(drink[sta[top]])drink2[belong[sta[top]]]=true; top--; } } } int viss[maxn],diss[maxn]; void spfa(int s){ queue<int> q; viss[s]=1;diss[s]=size[s]; q.push(s); while(!q.empty()){ int u=q.front();q.pop();viss[u]=0; for(int i=head2[u];i;i=edge2[i].next){ int v=edge2[i].to; if(diss[v]<diss[u]+size[v]){ diss[v]=diss[u]+size[v]; if(!viss[v]){ viss[v]=1; q.push(v); } } } } } int main(){ int m,n; scanf("%d%d",&n,&m); for(int i=1;i<=m;i++){ int from,to; scanf("%d%d",&from,&to); add(from,to); } for(int i=1;i<=n;i++){ scanf("%d",&val[i]); } int begin,dnum; scanf("%d%d",&begin,&dnum); for(int i=1;i<=dnum;i++){ int x; scanf("%d",&x); drink[x]=true; } for(int i=1;i<=n;i++){ tarjan(i); } for(int i=1;i<=m;i++){ if(belong[edge[i].from]!=belong[edge[i].to]){ add2(belong[edge[i].from],belong[edge[i].to]); } } //缩完后点之间的边 spfa(belong[begin]); int ans=0; for(int i=1;i<=belongcnt;i++){ if(drink2[i])ans=max(ans,diss[i]);//只有是酒吧才算最大值 } printf("%d",ans); return 0; }
题目:

简而言之,就是给你i个牛,每个牛可以清扫M到E,代价为S,问覆盖全部区间的最小代价(这不显然是线段树板子吗)
分析:
我们可以这么想,如果一头牛从i打扫到j,那么就从i到j+1建一条边(题目中说了牛打扫的是闭区间,所以我们建边时候要处理一下,把[i,j]变成[i,j+1)否则加边区间会重复)
然后呢,我们对于每一个i点,都建一条权值为0的i到i-1的边,然后从起点到终点跑最短路。
这是为什么呢?
我们想一想,如果有两头牛,他们分别打扫1->5,2->6,如果不建反向的权值为0的边,那么这个情况下1和6是不联通的,我们需要解决这种有重叠区间的问题的话,只要从5到2建一条权值为0的边,这样在跑最短路跑到5的时候,可以回到2继续跑。所以,我们的方案就是通过反向建0的边,使本来不联通的“重叠”区间也可以连起来,而且这样不会影响最后结果,之前不联通,这样操作还是不联通,因为反向建的边是单向的,只能从较后位置到较前位置。
代码:
#include<bits/stdc++.h> using namespace std; const int maxn=1e6+10; struct E{ int to,val,next; }edge[maxn]; int head[maxn],tot; void add(int from,int to,int val){ edge[++tot].to=to; edge[tot].val=val; edge[tot].next=head[from]; head[from]=tot; } int n,m,e; int vis[maxn],d[maxn]; void spfa(int s){ memset(d,0x3f,sizeof(d)); queue<int> q; d[s]=0;vis[s]=1;q.push(s); while(!q.empty()){ int u=q.front(); q.pop(); vis[u]=0; for(int i=head[u];i;i=edge[i].next){ int v=edge[i].to; if(vis[v])continue; if(d[v]>d[u]+edge[i].val){ d[v]=d[u]+edge[i].val; q.push(v); vis[v]=1; } } } } int main(){ scanf("%d%d%d",&n,&m,&e); for(int i=m;i<=e;i++){ add(i+1,i,0); } for(int i=1;i<=n;i++){ int from,to,val; scanf("%d%d%d",&from,&to,&val); to++; add(from,to,val); } spfa(m); if(d[e+1]==0x3f3f3f3f){ printf("-1"); return 0; } printf("%d",d[e+1]);//注意最后的区间变成了[m,e+1)而不是[m,e]了 return 0; }
题目:
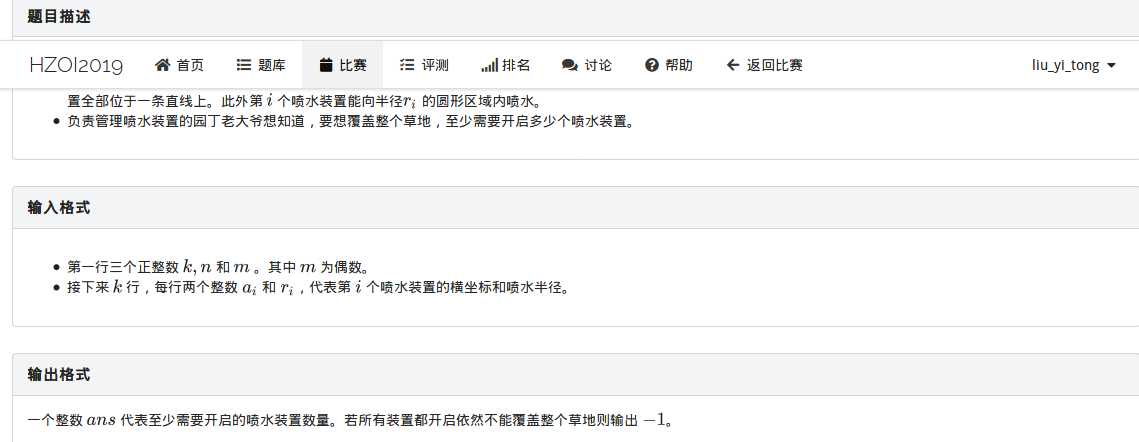
其实这道题是个贪心
分析:
我们可以这样考虑:每一个喷射装置覆盖一个圆形的面积,但是如果喷射半径小于m/2,那这个喷头相当于废了,它连自己的上下都喷不到,就不可能选它了,接着,面积什么的显然不好处理,还会有一些重叠就更不好了,我们可以把每个喷头所覆盖的n上面长度作为该喷头的“有效范围”,由于上下对称性,只要长方形的一条长被覆盖满了,另外一条必覆盖满,所以我们把这道题看作有n个喷头,每个喷头覆盖l到r,求覆盖所有区间的最小数量。
emm,这句话怎么这么熟悉?看了一下上一道题的描述(显然这两道题是一道题)
所以打出代码来,也跟上一道题是一样的,我就不放代码了
显然还是有一些区别的,比如这道题每一个喷头覆盖区间的左右端点是doube类型,不能直接当结点,会有蛋疼的精度问题,所以……
我们直接把每一个double值扩大一个倍数转成整形,相应的n也扩大,这样就可以代入上一道题的代码了。(×5就可以)
附上代码:
#include<bits/stdc++.h> using namespace std; const int maxn=1e7+10; int k,n,m; struct E{ int to,val,next; }edge[maxn]; int head[maxn],tot; void add(int from,int to,int val){ edge[++tot].to=to; edge[tot].val=val; edge[tot].next=head[from]; head[from]=tot; } int vis[maxn],d[maxn]; void spfa(int s){ memset(d,0x3f,sizeof(d)); queue<int> q; d[s]=0;vis[s]=1;q.push(s); while(!q.empty()){ int u=q.front(); //printf("%d ",u); q.pop(); vis[u]=0; for(int i=head[u];i;i=edge[i].next){ int v=edge[i].to; if(vis[v])continue; if(d[v]>d[u]+edge[i].val){ d[v]=d[u]+edge[i].val; q.push(v); vis[v]=1; } } } } int main(){ scanf("%d%d%d",&k,&n,&m); for(int i=1;i<=k;i++){ int aa,r; scanf("%d%d",&aa,&r); if(r<=m/2)continue; int ll=(int)(aa*5-sqrt(r*r-m*m/4)*5); int rr=(int)(aa*5+sqrt(r*r-m*m/4)*5); //区间变为:[当前位置×5-向左的距离×5,当前位置×5+向右的距离×5+1); //因为该区间相当于这个喷头覆盖范围的一个弦,所以左右延伸的距离(半弦长)=根号(半径平方-弦心距平方)/2; if(ll<0)ll=0; add(ll,rr+1,1); } for(int i=1;i<=n*25;i++)add(i,i-1,0); spfa(0); if(d[n*5+1]==0x3f3f3f3f)d[n*5+1]=-1; printf("%d",d[n*5+1]); return 0; }
(集训模拟赛8)升降梯上(分层图最短路)
题目大意:
有n层楼,你现在在第1层,有一个电梯,上面有个拉杆,有m个控制槽,槽上有数字,拨到哪个槽就上升相应层数(不能下降到<=0或上升到>n层),最开始拉杆在“0”槽位处,数字有正有负,且控制槽之间的数字是有顺序的,每移动一格控制槽需要1s,每上或下一层楼要2s,问走到顶楼的最小时间。
分析:(看起来是个dp,好像也可以推出来转移方程,但是会有一些小问题,这边只考虑正解(最短路)。)
我们把每种需要花费时间的操作当成边来处理,时间就是边的权值。
我们可以把每一层的每一个控制槽看作一个结点,它向本层的其它槽位的点建边(因为这需要话费时间),还向它指向的那一层的这个槽建一条边(同上),权值按照题目要求设定。(注意:二维的点(i,j)不适合作为图的结点,我们可以把每一个点的坐标处理一下,变成一维的点,然后剩下的操作就好处理了。)
主要步骤:
1.转点,第一层的点从1到m,第二层的点是m+1到2*m……第n层的点是(n-1)*m+1到n*m。
2.建边,每一个点向周围的槽位和自己指向的槽位建边。
3.最短路,需要从第一层的“0”槽到顶层的槽位中找最小值。
附上代码:
#include<bits/stdc++.h> using namespace std; const int maxn=1e6+10; struct E{ int from; int to,val,next; }edge[maxn]; int head[maxn],tot,dis[maxn],vis[maxn]; void add(int from,int to,int val){ edge[++tot].to=to; edge[tot].from=from; edge[tot].val=val; edge[tot].next=head[from]; head[from]=tot; } void spfa(int s){ memset(dis,0x3f,sizeof(dis));memset(vis,0,sizeof(vis)); dis[s]=0;vis[s]=1; queue<int> q; q.push(s); while(!q.empty()){ int u=q.front();q.pop();vis[u]=0; for(int i=head[u];i;i=edge[i].next){ int v=edge[i].to; if(dis[v]>dis[u]+edge[i].val){ dis[v]=dis[u]+edge[i].val; if(!vis[v]){ q.push(v);vis[v]=1; } } } } } int n,m,c[maxn]; int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=m;i++)scanf("%d",&c[i]);//每一个槽位及上面的数字 //建同一层之间的边 for(int now=1;now<=n;now++){ for(int i=1;i<=m;i++){ for(int d=0;d<=m-1;d++){ if(i+d<=m)add((now-1)*m+i,(now-1)*m+i+d,d); if(i-d>=1)add((now-1)*m+i,(now-1)*m+i-d,d); } } } //建层与层之间的边 for(int now=1;now<=n;now++){ for(int i=1;i<=m;i++){ if((now-1+c[i])*m+i<=n*m&&(now-1+c[i])*m+i>=1){//边界条件:不超过最大节点(n*m)不小于最小节点(1) if(c[i]==0)continue; add((now-1)*m+i,(now-1+c[i])*m+i,2*abs(c[i])); } } } int start=0; for(int i=1;i<=m;i++){ if(c[i]==0)start=i; } spfa(start); int Min=0x7fffffff; for(int i=1;i<=m;i++){ Min=min(Min,dis[(n-1)*m+i]); } if(Min==0x3f3f3f3f)Min=-1; printf("%d",Min); return 0; }
题目:
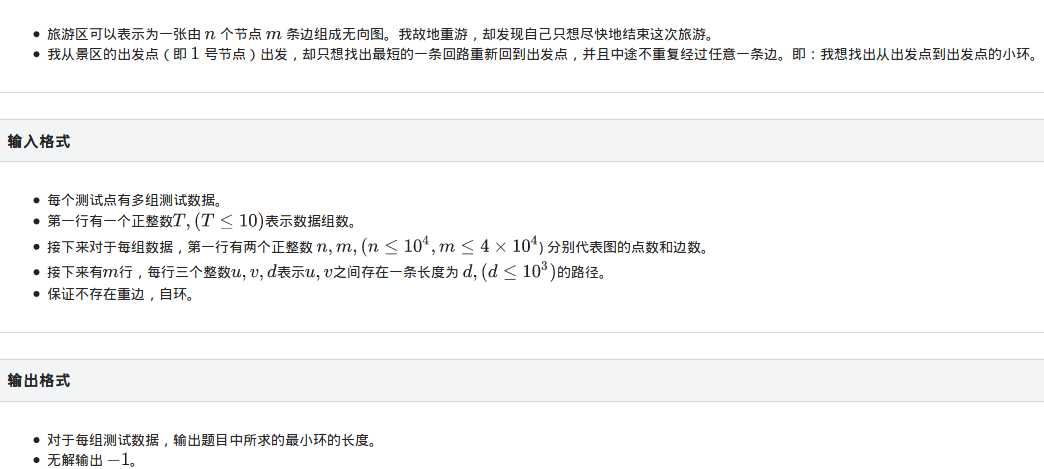
思路:
这道题要求求已知起点的一条最小环,边是无向的但每条边又只能走一次(一看到最小环不就应该知道是最短路了吗)
一般求最小环都是用floyd算法,详情请见老姚博客:https://www.cnblogs.com/hbhszxyb/p/12770720.html
这道题显然n3的效率会炸,所以我们需要另寻它法。
我们知道,一个简单环,断掉一条边就会形成一条链,我们可以利用这一点,尝试断掉某个点与起点相连的一条边,再求起点到它的最短路,那么到这个点的最短路+断掉的这条边权就是起点与这个点所在的环的大小了,我们枚举每一条与起点相连的边,并尝试断掉它,然后求环的大小,取最小值即可。
注意:每次断边要断两个,建议在建边时候按^1的方法去建(0、1是一对反向边,2、3是一对反向边,4、5是一对……),这样在断边时候好处理
附上代码:
#include<bits/stdc++.h> using namespace std; const int maxn=4e5+10; struct E{int to,next,val;}edge[maxn]; int head[maxn],tot,Min=0x3f3f3f3f; void add(int from,int to,int val){ edge[tot].to=to; edge[tot].val=val; edge[tot].next=head[from]; head[from]=tot++; } int d[maxn],vis[maxn]; void spfa(int s){ memset(d,0x3f,sizeof(d)); memset(vis,0,sizeof(vis)); queue<int> q; d[s]=0; q.push(s); while(!q.empty()){ int u=q.front();q.pop();vis[u]=0; for(int i=head[u];~i;i=edge[i].next){ int v=edge[i].to; if(d[v]>d[u]+edge[i].val){ d[v]=d[u]+edge[i].val; if(!vis[v]){ q.push(v); vis[v]=1; } } } } } int n,m,t,from,to,val; int main(){ scanf("%d",&t); while(t--){ memset(head,-1,sizeof(head));tot=0; scanf("%d%d",&n,&m); for(int i=1;i<=m;i++){ scanf("%d%d%d",&from,&to,&val); add(from,to,val); add(to,from,val); } Min=0x3f3f3f3f; for(int i=head[1];~i;i=edge[i].next){ int now=edge[i].val;//断掉这条边的边权 int v=edge[i].to;//某个与起点直接相连的点 edge[i].val=edge[i^1].val=0x3f3f3f3f;//断边(给它恢复初始值) spfa(1); Min=min(Min,d[v]+now); edge[i].val=edge[i^1].val=now;//再建回来 } if(Min==0x3f3f3f3f)Min=-1; printf("%d\n",Min); } return 0; }
标签:实现 区别 a* star 覆盖 line info http include
原文地址:https://www.cnblogs.com/liu-yi-tong/p/13277579.html