matlab cvx工具箱解决线性优化问题

标签：最大利润   来源   begin   lan   第二版   isp   mamicode   format   空间   

题目来源：数学建模算法与应用第二版（司守奎）第一章习题1.4

题目说明

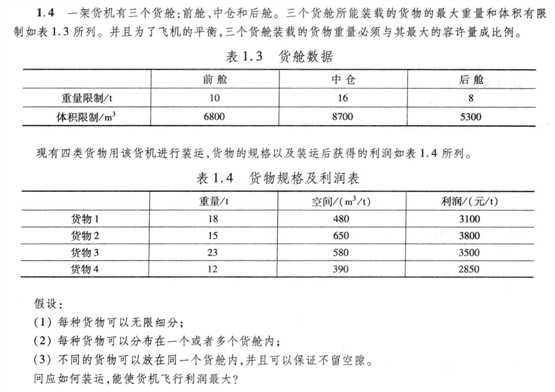
作者在答案中已经说明，求解上述线性规划模型时，尽量用Lingo软件，如果使用Matlab软件求解，需要做变量替换，把二维决策变量化成一维决策变量，很不方便。（原答案附末尾）

这里我们可以采用matlab的cvx工具箱进行编写，会简化代码并提升可读性

clc;clear;
format short;
% 初始数据
w = [18 15 23 12];
r = [3100 3800 3500 2850] .* w;
s = [480 650 580 390] .* w;
ls = [6800 8700 5300];
lw = [10 16 8];

%开始求解
cvx_begin  
    variable x(4,3); 	% 决策变量
    maximize(sum(r*x)); % 目标函数
    subject to          % 约束条件
        w*x<=lw;
        s*x<=ls;
        x >= 0;
        sum(x,2) <= 1     
cvx_end  

disp("每种货物吨数(t)：");
result = w‘ .* sum(x,2);
disp(result);
disp(‘最大利润(元):‘);
disp(cvx_optval);

代码说明：

w为每种货物的总重量

r为每种货物的总利润

s为每种货物所占用的总空间

ls为飞机上的空间限制

ls为飞机上的重量限制

运行结果：

原版答案：

matlab cvx工具箱解决线性优化问题

标签：最大利润   来源   begin   lan   第二版   isp   mamicode   format   空间   

原文地址：https://www.cnblogs.com/aminor/p/13280637.html