标签:mat log max 滑动 转移 思考 family 简单的 滚动
处处是被放大的悲伤,次次是被遗忘的梦想,总苦恼于生不逢时,却记不得自己是怎样的坚强。
July 3rd 2020
关于线性dp,基本上大部分的dp都是从线性的dp变化而来的,线性dp从我们刚入门开始,一直陪伴到我们入土,就已经有所涉及了,本文讲的主要是序列上的线性dp,也就是基于给定的数列进行我们的状态设定,转移方程。线性dp并不是说给定的序列一定是线性的,只要我们的转移的过程是线性的,就可以称之为线性dp。
说到序列类的线性dp,我们通常会想到这几道比较基础的题——数字三角形,LIS,LCS,LCIS,多数上是基于序列上的数,在之间加上限制影响,然后得到最大/最小的值,根据变通,可能会转化成矩阵,图等,需要很强的变通能力,说白了,需要的是刷题,刷题,刷题,经验和思考方式来自于刷题。
本篇主要讲有关于求和求值类的DP,其余的就一带而过啦,有兴趣的朋友可以去百度其他大佬(其实只是因为懒
特定条件的序列选择
1.LCS、LIS、LCIS。
其实都挺简单不是嘛…………,每次都扫一遍前面,找一个最大的转移,这里有个小优化,有的可以考虑加一个单调队列,后面再讲。
2.最大区间子段和。
此外还有带修改的查询区间最大子段和,用线段树维护即可,维护信息有——从左端点开始的连续最大子段和,从右端点开始的连续最大子段和,最大字段和,区间和四个信息,往上转移就好~
3.包装起来的题。
子矩阵一题中状压后便为序列类线性dp,对于每个状态对应一个序列,转化为求序列中选k个数,每相邻两个数的绝对值之和
洛谷P1052 过河
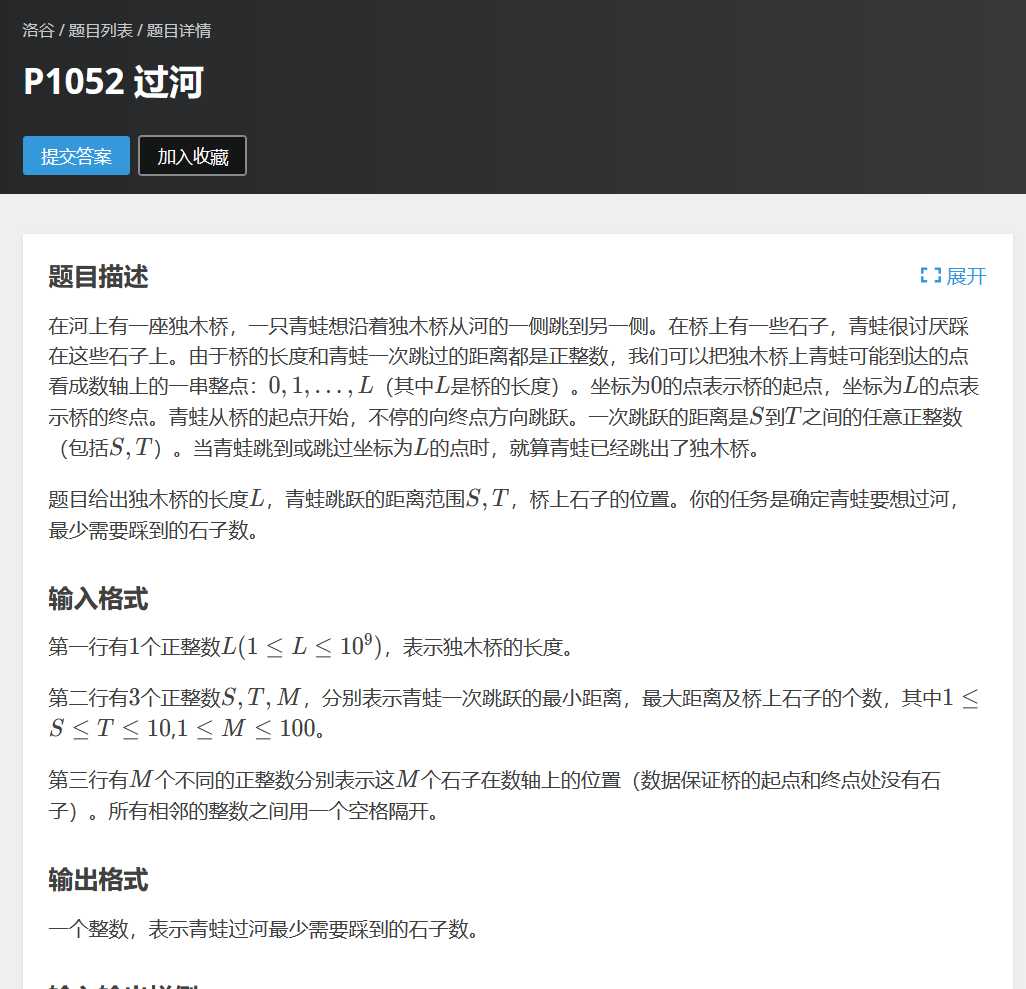
此题运用一个定理——裴蜀定理即可解决,

ax+by所不能表示出的最大整数就是9*10-9-10=71,所有大于71的都可被缩成71解决就行了,emmmmm,讲石头之间距离缩成71的意思就是将所有组合的可能全部考虑到,即:71后面的步数都可以被组合出来,我们可以考虑到所有飞过该石头的转移状态,其他的调整ax+by就可以被表示出来,所以不会有遗漏的转移。

#include<bits/stdc++.h> using namespace std; #define ll long long ll n,d,k,ans=-1; const ll N=500005; ll dp[N],q[N],s[N],score[N]; template<typename dr> void read(dr &a){ dr x=0,f=1;char ch=getchar(); for(;!isdigit(ch);ch=getchar())if(ch==‘-‘)f=-1; for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-‘0‘; a=x*f; } bool check(ll mid){ memset(dp,-0x3f,sizeof(dp)); memset(q,0,sizeof(q)); dp[0]=0; ll l=1,r=1,j=1; for(ll i=1;i<=n;i++){ for(;j<i&&s[i]-s[j]>=d-mid;j++){ while(l<r&&dp[q[r]]<=dp[j])--r; q[++r]=j; } while(l<r&&s[i]-s[q[l]]>d+mid)l++; while(l<r&&dp[q[l+1]]>dp[q[l]]&&s[i]-s[q[l+1]]>=max(d-mid,1ll))l++; if(s[i]-s[q[l]]<d-mid||s[i]-s[q[l]]>d+mid)continue; dp[i]=dp[q[l]]+score[i]; if(dp[i]>=k)return 1; } //printf("%lld %lld\n",mid,cnt); return 0; } int main() { read(n),read(d),read(k); for(ll i=1;i<=n;i++)read(s[i]),read(score[i]); ll l=0,r=s[n]; while(l<=r){ ll mid=l+r>>1; if(check(mid))ans=mid,r=mid-1; else l=mid+1; } printf("%lld\n",ans); return 0; }
洛谷P1866 滑动窗口
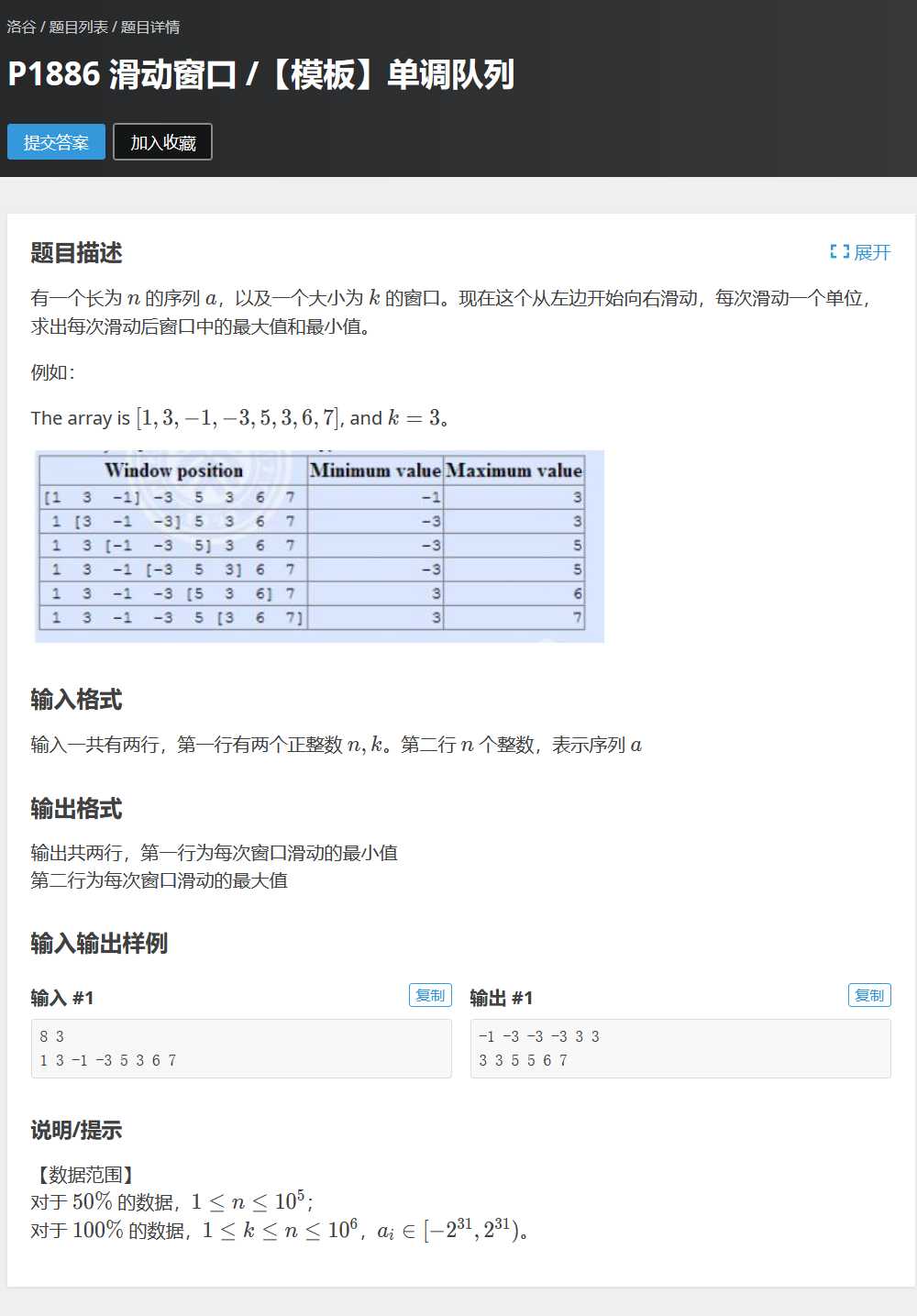
引用机房韦大佬的一句话:单调队列?就是单调的队列啦~~~
单调队列的模板题,对于每次我们要的答案,我们只需要保存保证对当前答案可能有贡献的值,即:坐标靠后,且较大的值,如若队头已经超出窗口范围队头向后挪动即可,考虑每次加进来的值,如果大于当前的队尾,则这个队尾就没什么卵用了,把它弹掉即可,最后我们的队列是坐标递增、数值递减的(反之亦然,坐标递增、数值递增),所以称之为单调队列。考虑时间复杂度,每个值只会进队一次,也只会出队一次,所以只有O(N)
这么简单的就不贴代码了吧,(其实是因为我没写
接下来可以考虑将单调队列运用到dp之中。
洛谷P3957 跳房子

这题算是普及组里比较难的一题动态规划了,当然现在再来看看还算正常,毕竟摆渡车都出来了,还有什么好编排的,CCF你彳亍啊,CSP三紫两黑逼着洛谷下降难度,考虑到g无法确定,这里建议二分处理哦亲~,范围自然就是0到最大的那个了,也不大,每次dp一遍,只要分数够了就返回,dp过程将能跳到这个点的格子加入队尾,然后从队头检查,将不符合条件的弹掉就行了。

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define ll long long 4 ll n,d,k,ans=-1; 5 const ll N=500005; 6 ll dp[N],q[N],s[N],score[N]; 7 template<typename dr> void read(dr &a){ 8 dr x=0,f=1;char ch=getchar(); 9 for(;!isdigit(ch);ch=getchar())if(ch==‘-‘)f=-1; 10 for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-‘0‘; 11 a=x*f; 12 } 13 bool check(ll mid){ 14 memset(dp,-0x3f,sizeof(dp)); 15 memset(q,0,sizeof(q)); 16 dp[0]=0; 17 ll l=1,r=1,j=1; 18 for(ll i=1;i<=n;i++){ 19 for(;j<i&&s[i]-s[j]>=d-mid;j++){ 20 while(l<r&&dp[q[r]]<=dp[j])--r; 21 q[++r]=j; 22 } 23 while(l<r&&s[i]-s[q[l]]>d+mid)l++; 24 while(l<r&&dp[q[l+1]]>dp[q[l]]&&s[i]-s[q[l+1]]>=max(d-mid,1ll))l++; 25 if(s[i]-s[q[l]]<d-mid||s[i]-s[q[l]]>d+mid)continue; 26 dp[i]=dp[q[l]]+score[i]; 27 if(dp[i]>=k)return 1; 28 } 29 //printf("%lld %lld\n",mid,cnt); 30 return 0; 31 } 32 int main() 33 { 34 read(n),read(d),read(k); 35 for(ll i=1;i<=n;i++)read(s[i]),read(score[i]); 36 ll l=0,r=s[n]; 37 while(l<=r){ 38 ll mid=l+r>>1; 39 if(check(mid))ans=mid,r=mid-1; 40 else l=mid+1; 41 } 42 printf("%lld\n",ans); 43 return 0; 44 }
由上可知,当序列类DP从上一个状态j转移过来的值以及增值只是分别与其中一项(i、j)有关的时候,形如f[i]=f[j]+b[i]这样的dp方程,可以使用单调队列优化,妥妥地。
但是,如果是b[i]*c[j]呢?,似乎没有什么好办法来保证你的结果就是最优了呢~(幸灾乐祸的毒瘤出题人)于是各路大佬给出了算法——
洛谷P3195 玩具装箱

依旧是话不多说先上模板题,如果已经拥有灰常丰富的dp经验的大佬很快就能写出dp的转移方程式:f[i]=f[j]+(i-j-1+sumc[i]-sumc[j]-L)²,(i-j-1是因为j这个位置并不算在内),展开之后又有i又有j的实在让人头疼,怎么办?展开再说呗,不展开说个桃子,为了方便计算和说明,我们设i+sumc[i]=A[i],j+sumc[j]+L+1=B[i],原式化为f[i]=f[j]+A[i]²-2*A[i]*B[j]+B[j]²。按照算法,我们将式子化为我们想要的样子,斜率优化,自然是依靠斜率,则形如一次函数y=kx+b才有斜率。即——f[i]-A[i]+2*A[i]*B[j]=f[j]+B[j]²,f[i]-A[i]当作是b,2*A[i]为k,则B[i]就是x,f[j]+B[j]²为y,一般我们是把只和i有关的项作为常数,只和j有关的项作为y函数值,因为这样可以计算(不然要算出i然后再计算,这样显得本末倒置,毫无意义,而且斜率优化之中要求的值与常数项有关,后面再讲),接下来我们将图像画到坐标轴上理解。
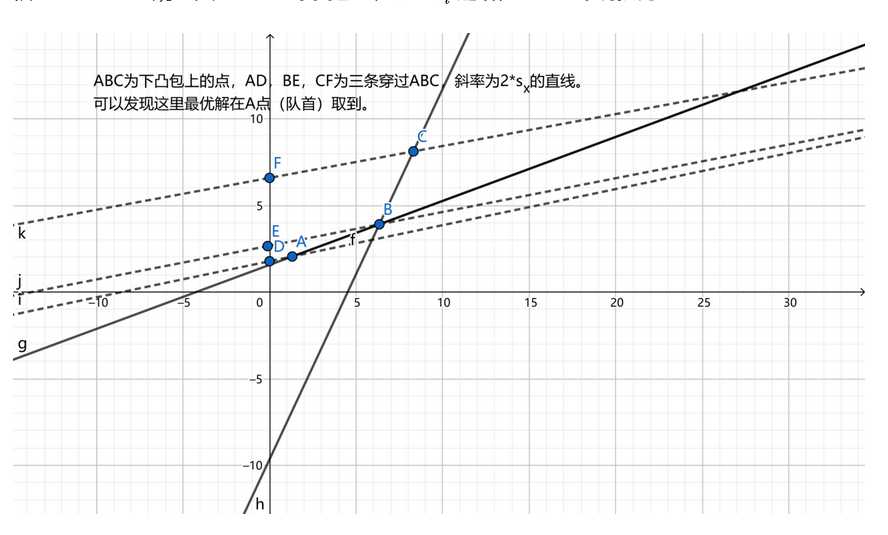
如上图,我们想让f[i]尽可能小,那么对于斜率固定的函数而言,那么——
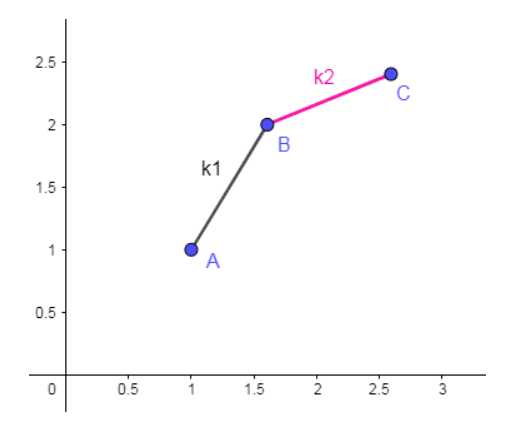
当我们的点有这种情况的时候,显然B点不会成为最优解,这时候要维护使得斜率递增才能保证不会出现上凸壳,相反如果你要是想求最大值,就要保证不会出现下凸壳。
那么我们如何取队头呢?我们还是根据图来观察
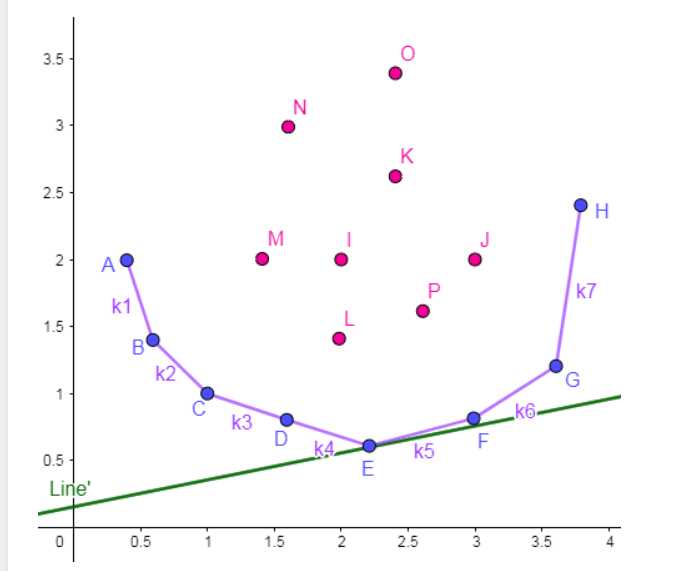
上图中可以发现,当E、F两点之间连成直线的斜率刚好大于我们的函数斜率k的时候,E是最优的,所以遇到小于斜率的弹掉就行,也可以直接计算f[i]的值进行比较,直至队头算出的值已经成为最优。
斜率则用单调队列或者单调栈来维护,二者区别在于转换成一次函数后的直线y=kx+b中斜率k的递减与递增及对应的凸壳(维护的凸壳取决于要求的是最大值还是最小值),若斜率k递增,维护的是上凸壳,或者斜率k递减,维护的是下凸壳,画图可知靠前的点反而更有潜力更新答案,即所求解必须从后往前寻找第一个大于/小于斜率k的点,操作都在队尾,所以要使用单调栈来维护;若是斜率k递减维护上凸壳,或者斜率k递增维护下凸壳,对于我们维护的队列中斜率亦是递减或递增,则就要从队头找起,需要使用单调队列维护;若中斜率k递减与递增不定,我们只能维护整个凸壳,二分查找转移点j了。若x坐标的增减性不再固定,因为我们不知道该在何处插入我们的新点,就要使用数据结构平衡树或者CDQ分治来解决了,超出了蒟蒻我的范畴,(呜呜呜我好菜
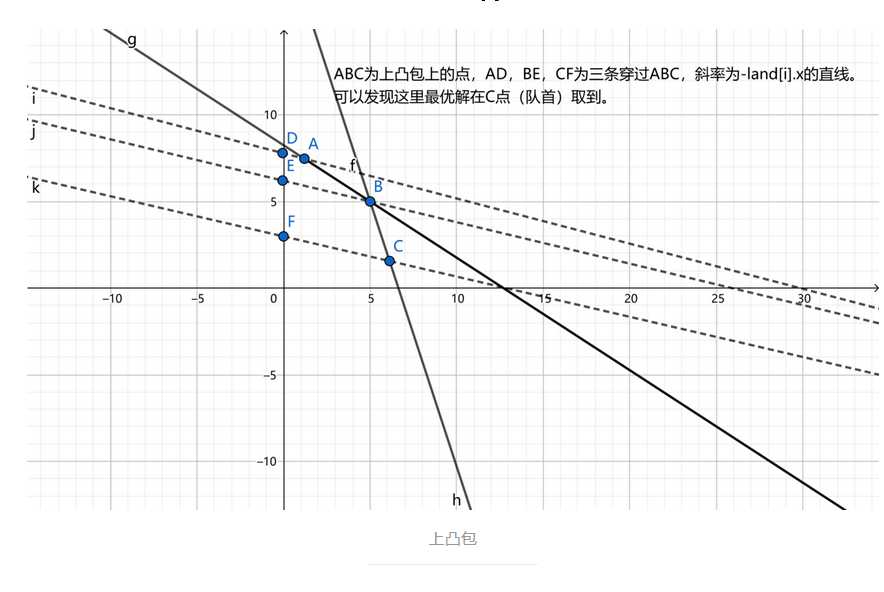
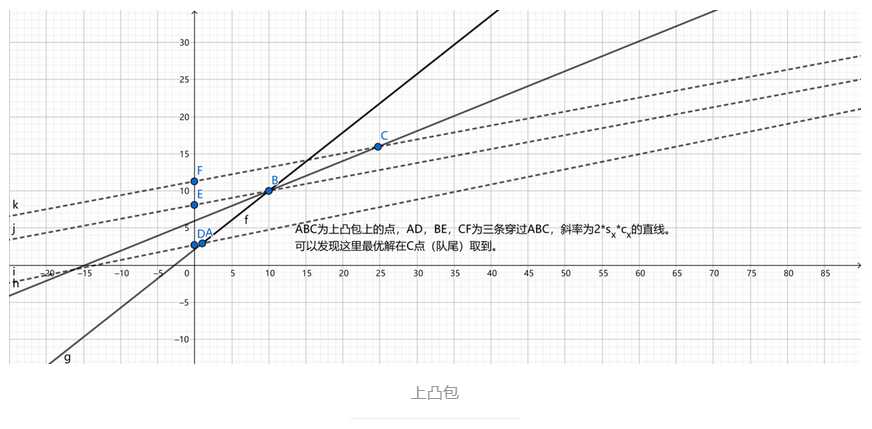
若最优决策点横坐标靠后则单调栈维护,靠前则单调队列维护。
该讲的都讲完了,接下来就是本题的代码了。

#include<bits/stdc++.h> using namespace std; #define ll long long #define N 500005 #define ld long double #define X(i) (i+sum[i]) #define Y(j) (j+sum[j]+L+1) ll dp[N],sum[N],L; ld Q[N]; ld slope(ll y,ll x){return (ld)((dp[y]+Y(y)*Y(y)-dp[x]-Y(x)*Y(x) )/ (Y(y)-Y(x)));} template <typename dr> void read(dr &a){ dr x=0,f=1;char ch=getchar(); for(;!isdigit(ch);ch=getchar())if(ch==‘-‘)f=-1; for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-‘0‘; a=x*f; } int main() { ll n; read(n),read(L); for(ll i=1;i<=n;i++){ read(sum[i]);sum[i]+=sum[i-1]; } ll head=1,tail=1; for(ll i=1;i<=n;i++){ while(head<tail&&slope(Q[head],Q[head+1])<=2*X(i))++head; int j=Q[head]; dp[i]=dp[j]+(X(i)-Y(j))*(X(i)-Y(j)); while(head<tail&&slope(Q[tail],i)<slope(Q[tail-1],Q[tail]))--tail; Q[++tail]=i; } printf("%lld\n",dp[n]); return 0; }
P2635 任务安排1
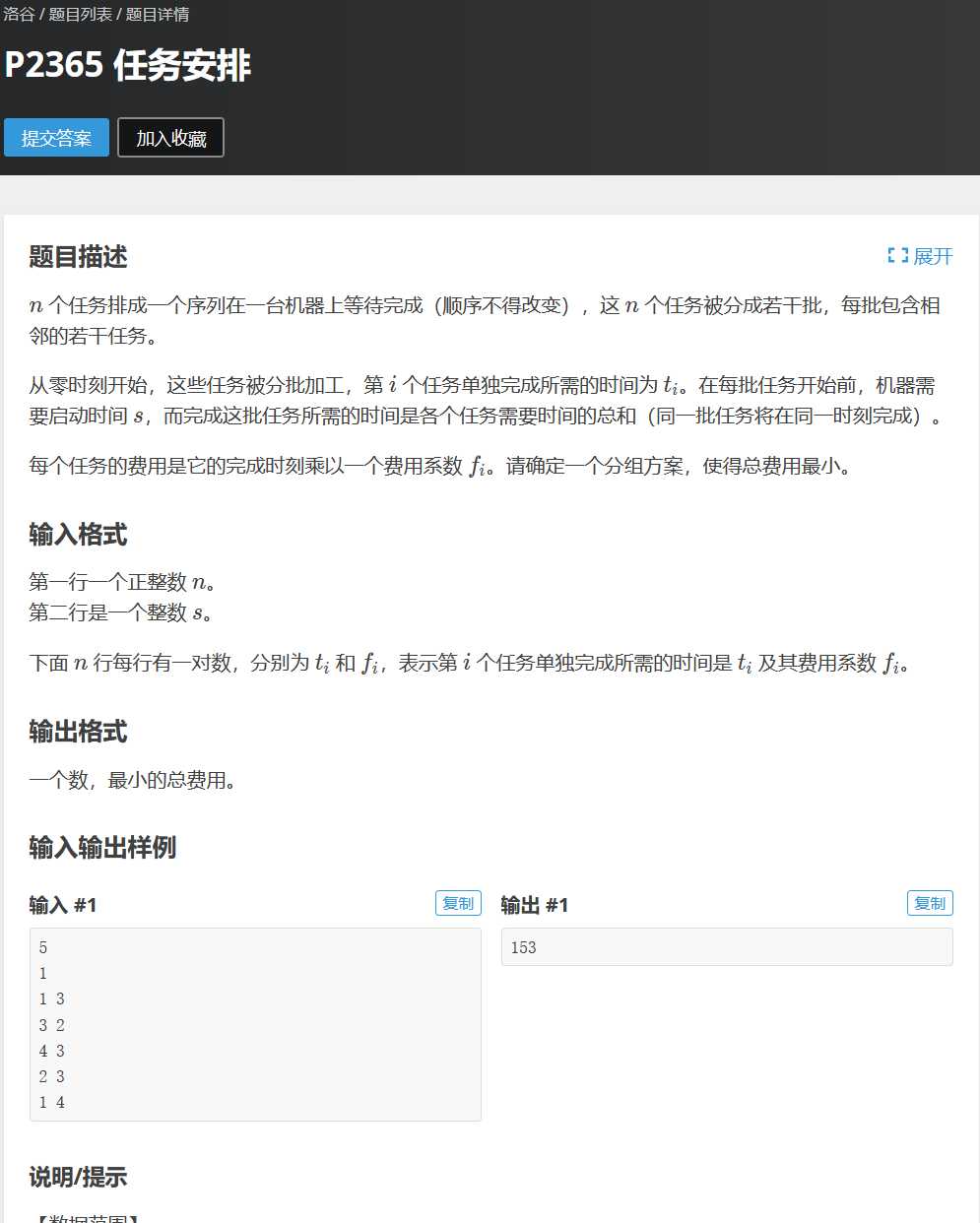
这题有些巧妙,因为分的批数是不定的,所有我们为了避免算后面的时候要用到前面分了多少批这个状态,我们采用费用提前的思想,在处理前面时把S产生的费用给计算了。即j状态后面的所有的任务的费用系数*s加入我们的答案中来,这样可以直接忽略掉启动时间s,当作没看见((((,转移方程不难写出:f[i]=f[j]+sumt[i]*(sumf[i]-sumf[j])+s*(sumf[n]-sumf[j])。这里费用提前计算的思想尤为巧妙,像我这样的蒟蒻只能远观膜拜,%%%tql。

#include<bits/stdc++.h> using namespace std; #define ll long long #define N 50005 ll n,s,t[N],c[N],dp[N],Q[N]; template <typename dr>void read(dr &a){ dr x=0,f=1;char ch=getchar(); for(;!isdigit(ch);ch=getchar())if(ch==‘-‘)f=-1; for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-‘0‘; a=x*f; } int main() { read(n);read(s); for(int i=1;i<=n;i++){ read(t[i]);read(c[i]); t[i]+=t[i-1];c[i]+=c[i-1]; } ll l=1,r=1; for(int i=1;i<=n;i++){ while(l<r&&dp[Q[l+1]]-dp[Q[l]]<=(s+t[i])*(c[Q[l+1]]-c[Q[l]]))l++; dp[i]=dp[Q[l]]+t[i]*c[i]+s*c[n]-c[Q[l]]*(s+t[i]); while(l<r&&(dp[i]-dp[Q[r]])*(c[Q[r]]-c[Q[r-1]])<=(dp[Q[r]]-dp[Q[r-1]])*(c[i]-c[Q[r]]))r--; Q[++r]=i; } printf("%lld\n",dp[n]); return 0; }
洛谷P5785 任务安排2
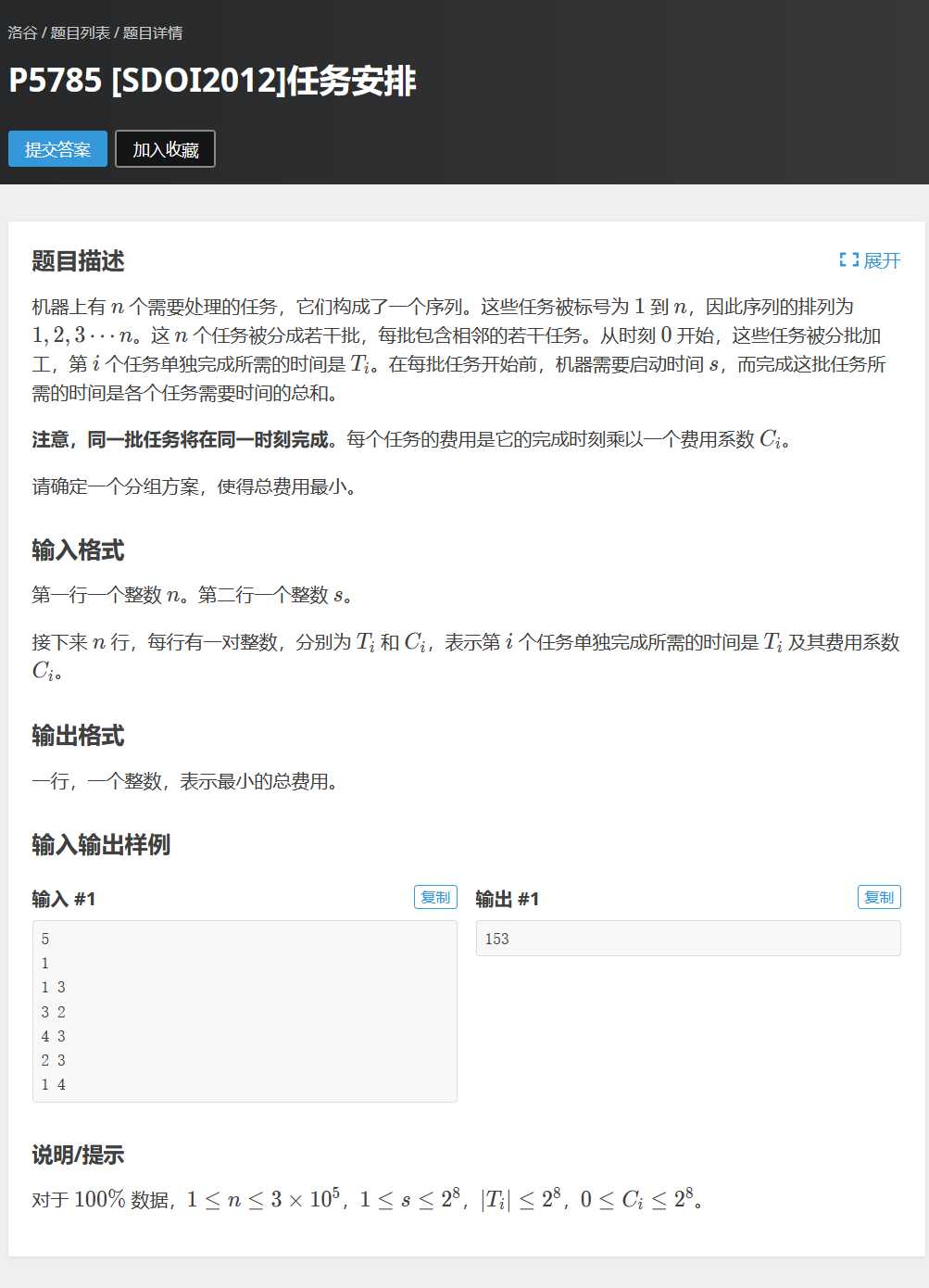
没错!这就是2.0版的玄学之处,我们的China制造工厂生产机器已经超越光速啦(…啦…啦...啦……啦),它在加工某些神器的反物质态物品可以让全村的人们见到卖火柴小女孩的奶奶,可以让时空倒流,所以加工时间T现在可以为负,也就是前面说的,直线kx+b的斜率不再递增或递减,而是飘忽不定的k~二分查找即可。

#include<bits/stdc++.h> using namespace std; #define ll long long #define N 500005 ll n,s,t[N],c[N],dp[N],Q[N]; template <typename dr>void read(dr &a){ dr x=0,f=1;char ch=getchar(); for(;!isdigit(ch);ch=getchar())if(ch==‘-‘)f=-1; for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-‘0‘; a=x*f; } int main() { read(n);read(s); for(int i=1;i<=n;i++){ read(t[i]);read(c[i]); t[i]+=t[i-1];c[i]+=c[i-1]; } ll l=1,r=1; for(int i=1;i<=n;i++){ ll ls=0,rs=r,mid,res=-1; while(ls<rs){ mid=ls+rs>>1; if((dp[Q[mid+1]]-dp[Q[mid]])>=(s+t[i])*(c[Q[mid+1]]-c[Q[mid]]))rs=mid; else ls=mid+1; } if(res==-1)res=rs; dp[i]=dp[Q[res]]+t[i]*c[i]+s*c[n]-c[Q[res]]*(s+t[i]); while(l<r&&(dp[i]-dp[Q[r]])*(c[Q[r]]-c[Q[r-1]])<=(dp[Q[r]]-dp[Q[r-1]])*(c[i]-c[Q[r]]))r--; Q[++r]=i; } printf("%lld\n",dp[n]); return 0; }
洛谷P5017 摆渡车
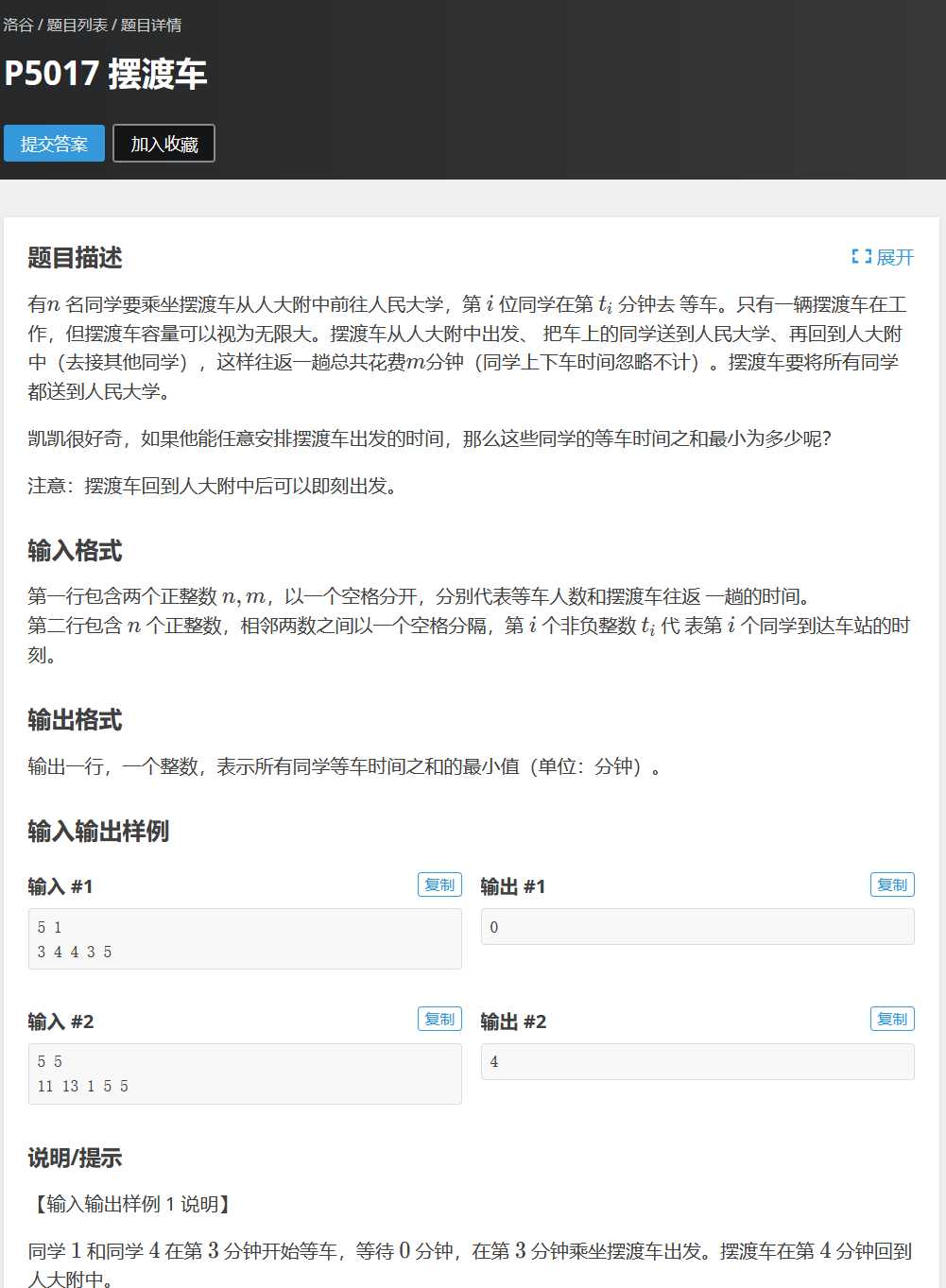
值得一题,此题有多种优化,可以路径压缩(大于两个同学之间大于2*m的可以考虑省掉直接改成2*m),再进行斜率优化(直接斜率优化也行),被我与机房大佬2014X戏谑称之为——“跳河车”
这题只要将时间轴画出便可看出是序列类dp,转移方程较为简单,为了防止转移状态不合法,我们转移到i的时候再将i-m的状态放入队列即可。

#include<bits/stdc++.h> using namespace std; #define ll long long const int N=4e6+5; ll sum[N],tim[N],a[1006],q[N],dp[N]; template<typename dr> void read(dr &a) { dr x=0,f=1;char ch=getchar(); for(;!isdigit(ch);ch=getchar())if(ch==‘-‘)f=-1; for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-‘0‘; a=x*f; } int main() { ll n,m,t=0; read(n),read(m); for(ll i=1;i<=n;i++){ read(a[i]);sum[a[i]]++;tim[a[i]]+=a[i]; t=max(t,a[i]); } for(ll i=1;i<t+m;i++)sum[i]+=sum[i-1],tim[i]+=tim[i-1]; ll l=1,r=0; for(ll i=0;i<t+m;i++){ if(i-m>=0){ while(l<r&&(dp[q[r]]+tim[q[r]]-dp[q[r-1]]-tim[q[r-1]])*(sum[i-m]-sum[q[r]])>=(dp[i-m]+tim[i-m]-dp[q[r]]-tim[q[r]])*(sum[q[r]]-sum[q[r-1]]))r--; q[++r]=i-m; } while(l<r&&(dp[q[l+1]]+tim[q[l+1]]-dp[q[l]]-tim[q[l]])<=i*(sum[q[l+1]]-sum[q[l]]))l++; ll j=q[l]; dp[i]=sum[i]*i-tim[i]; if(l<=r)dp[i]=min(dp[i],dp[j]+(sum[i]-sum[j])*(i)-tim[i]+tim[j]); } ll ans=1e9; for(ll i=t;i<t+m;i++)ans=min(ans,dp[i]); printf("%lld\n",ans); return 0; }
洛谷P2120 仓库建设

这题没什么特别的,非常中规中矩的一道练习题。

#include<bits/stdc++.h> using namespace std; #define ll long long #define N 1000005 ll sump[N],c[N],s[N],x[N],dp[N],q[N]; template<typename dr>void read(dr &a){ dr x=0,f=1;char ch=getchar(); for(;!isdigit(ch);ch=getchar())if(ch==‘-‘)f=-1; for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-‘0‘; a=x*f; } long double slope(ll x,ll y){ return (long double)(dp[y]+s[y]-dp[x]-s[x])/(sump[y]-sump[x]); } int main(){ ll n; read(n); for(ll i=1;i<=n;i++){ read(x[i]);read(sump[i]);read(c[i]); s[i]=s[i-1]+x[i]*sump[i];sump[i]+=sump[i-1]; //printf("%lld %lld %lld\n",x[i],sump[i],s[i]); } ll l=1,r=1; for(ll i=1;i<=n;i++){ while(l<r&&slope(q[l],q[l+1])<=x[i])l++; dp[i]=dp[q[l]]+(sump[i-1]-sump[q[l]])*x[i]-(s[i-1]-s[q[l]])+c[i]; while(l<r&&slope(q[r-1],q[r])>=slope(q[r],i))r--; q[++r]=i; } printf("%lld\n",dp[n]); return 0; }
洛谷P3628 特别行动队
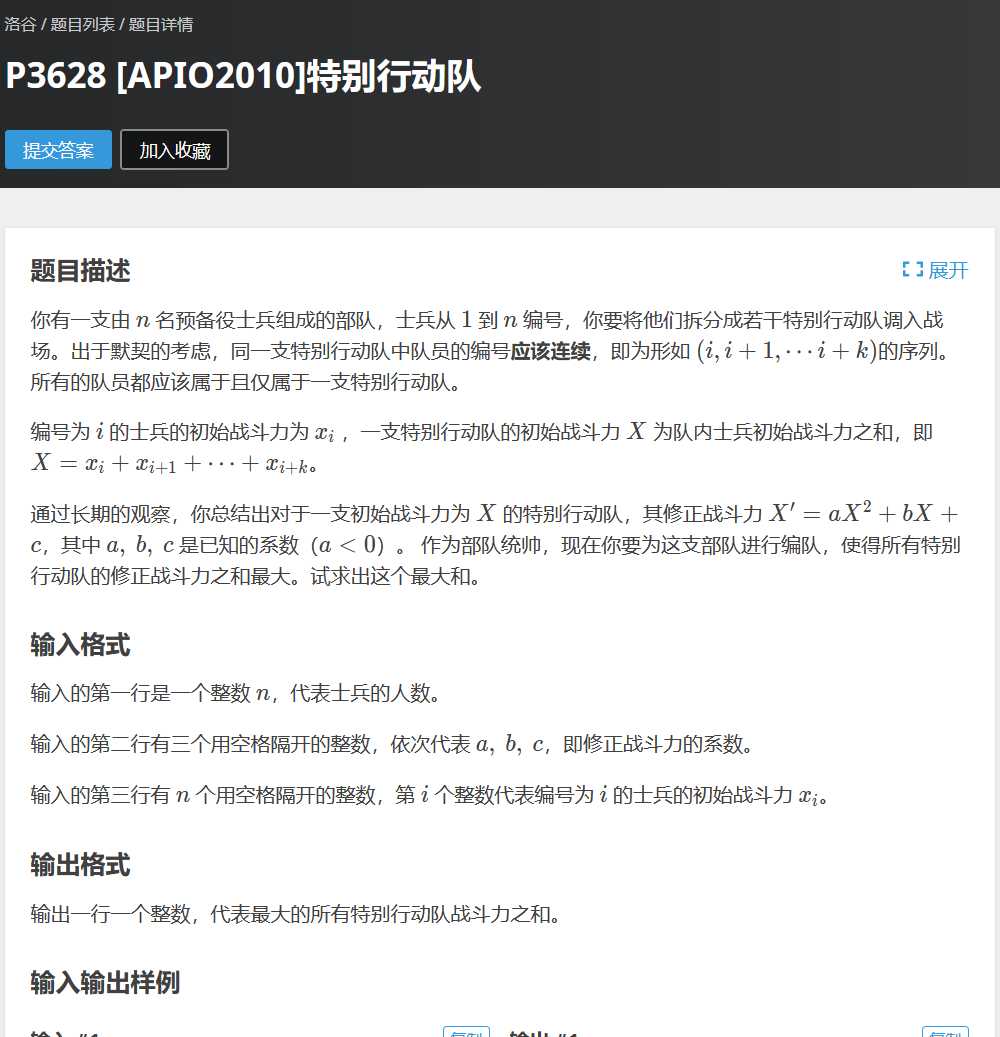
这题求得是最大,维护的是上凸壳,2014X大佬觉得把坐标反过来取下凸壳也行,我觉得还是老老实实的画图比较利于理解

#include<bits/stdc++.h> using namespace std; #define ll long long #define X(j) (sumx[j]) #define Y(j) (f[j]+a*sumx[j]*sumx[j]-b*sumx[j]) const ll N=1e6+5; ll f[N],q[N],a,b,c,sumx[N]; template<typename dr>void read(dr &a){ dr x=0,f=1;char ch=getchar(); for(;!isdigit(ch);ch=getchar())if(ch==‘-‘)f=-1; for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-‘0‘; a=x*f; } int main() { ll n; read(n); read(a);read(b);read(c); for(ll i=1;i<=n;i++){ read(sumx[i]);sumx[i]+=sumx[i-1]; } ll l=1,r=1; for(ll i=1;i<=n;i++){ while(l<r&&(Y(q[l+1])-Y(q[l]))>=2*a*sumx[i]*(X(q[l+1])-X(q[l])))l++; f[i]=f[q[l]]+a*(sumx[i]-sumx[q[l]])*(sumx[i]-sumx[q[l]])+b*(sumx[i]-sumx[q[l]])+c; while(l<r&&(Y(q[r])-Y(q[r-1]))*(X(i)-X(q[r]))<=(Y(i)-Y(q[r]))*(X(q[r])-X(q[r-1])))r--; q[++r]=i; } printf("%lld\n",f[n]); return 0; }
洛谷P4360 锯木厂选址
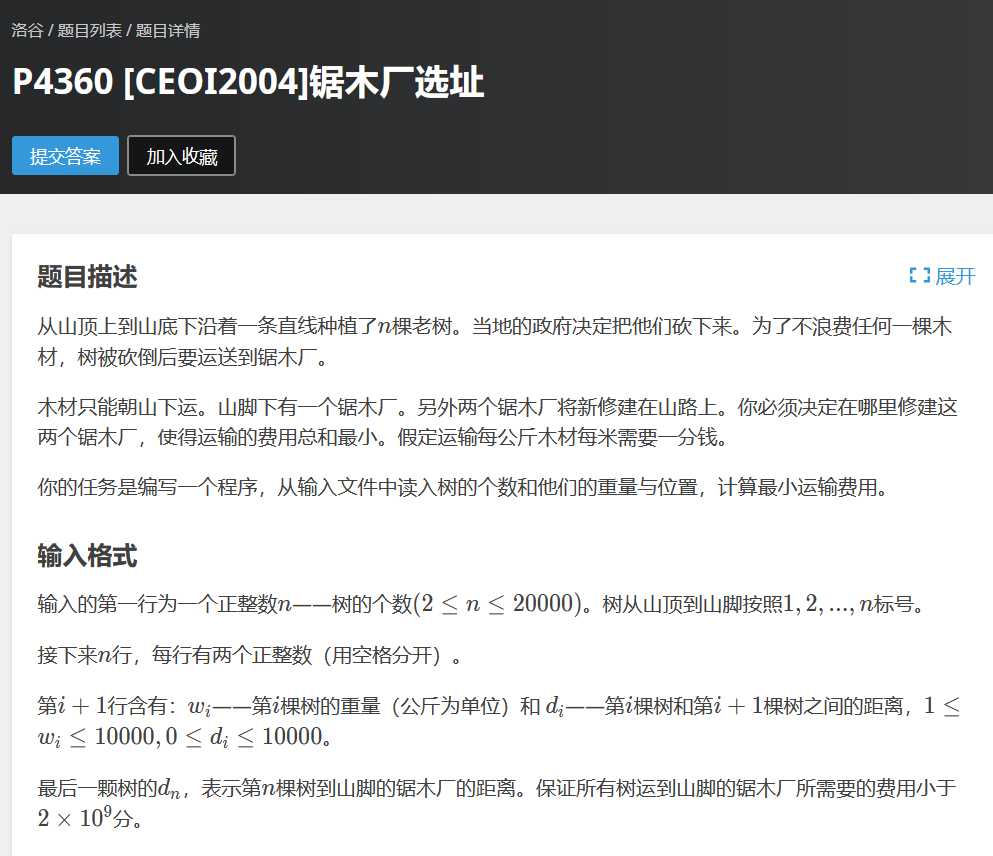
本来遇到这题我想是建两个单调队列的,结果突然发现我只用考虑第一个建在哪,另一个完全不需要放到队列里,最后就成了emmmm看起来比较奇怪的样子了,如果从前往后算的话,无法知道后面的木材运往山下的影响,这是有必要考虑进去的,所以使用了后缀和,从前往后看比较难看的时候,可以试着总花费减去节省的花费这种方式来推导。

#include<bits/stdc++.h> using namespace std; #define ll long long #define N 20005 #define Y(j) (d[j]*sw[j]) #define X(j) (sw[j]) ll ans,sum,sw[N],w[N],d[N],q[N],f[N]; template<typename dr>void read(dr &a){ dr x=0,f=1;char ch=getchar(); for(;!isdigit(ch);ch=getchar())if(ch==‘-‘)f=-1; for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-‘0‘; a=x*f; } int main() { ll n,ans=1e9; read(n); for(int i=1;i<=n;i++){ read(w[i]);read(d[i]); sw[i]=sw[i-1]+w[i]; } for(int i=n;i>=1;i--)d[i]+=d[i+1]; for(int i=1;i<=n;i++)sum+=d[i]*w[i]; ll l=1,r=1; for(int i=1;i<=n;i++){ while(l<r&&Y(q[l+1])-Y(q[l])>d[i]*(X(q[l+1])-X(q[l])))l++; ans=min(ans,sum-d[q[l]]*sw[q[l]]-d[i]*(sw[i]-sw[q[l]])); while(l<r&&(Y(q[r])-Y(q[r-1]))*(X(i)-X(q[r]))<(Y(i)-Y(q[r]))*(X(q[r])-X(q[r-1])))r--; q[++r]=i; } printf("%lld\n",ans); return 0; }
洛谷CF311B Cats Transport

这题算是一道比较有意思的题目了,首先为了方便我们一次性计算在某时刻派出我们的铲屎官可以带走多少只猫,以及这些猫等待的时间和,我们将猫结束的时间减去赶到它所在山丘要花的时间,这样就相当于把所有猫放在了一起,诚然就没山丘什么事了,其次对于派出的第p个铲屎官要从p-1个铲屎官转移过来,所以要建p个单调队列。

#include<bits/stdc++.h> using namespace std; #define ll long long #define N 100005 ll n,m,p,sd[N],t[N],dp[101][N],q[101][N],st[N],l[105],r[105]; template<typename dr> void read(dr &a){ dr x=0,f=1;char ch=getchar(); for(;!isdigit(ch);ch=getchar())if(ch==‘-‘)f=-1; for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-‘0‘; a=x*f; } int main() { read(n),read(m),read(p); for(ll i=2;i<=n;i++)read(sd[i]),sd[i]+=sd[i-1]; for(ll i=1;i<=m;i++){ ll x; read(x);read(t[i]); t[i]-=sd[x]; } if(p>=m)return putchar(‘0‘),0; sort(t+1,t+1+m); for(ll i=1;i<=m;i++)st[i]=st[i-1]+t[i]; for(ll i=1;i<=m;i++){ for(ll j=p;j>=1;j--){ while(l[j-1]<r[j-1]&&(dp[j-1][q[j-1][l[j-1]+1]]+st[q[j-1][l[j-1]+1]]-dp[j-1][q[j-1][l[j-1]]]-st[q[j-1][l[j-1]]])<=t[i]*(q[j-1][l[j-1]+1]-q[j-1][l[j-1]]))++l[j-1]; ll tr=q[j-1][l[j-1]]; dp[j][i]=dp[j-1][tr]+t[i]*(i-tr)-(st[i]-st[tr]); while(l[j]<r[j]&&(dp[j][q[j][r[j]]]+st[q[j][r[j]]]-dp[j][q[j][r[j]-1]]-st[q[j][r[j]-1]])*(i-q[j][r[j]])>=(dp[j][i]+st[i]-dp[j][q[j][r[j]]]-st[q[j][r[j]]])*(q[j][r[j]]-q[j][r[j]-1]))--r[j]; q[j][++r[j]]=i; } } printf("%lld\n",dp[p][m]); return 0; }
洛谷P2900 土地购买
讲真的这题我是瞪大了我的双眼也没看出来它是个斜率优化,愣是把我看傻了,其实如果自己想一想优化的话就可以看出来了,首先如果有一块土地的长和宽都小于另一块土地,那么这块土地就可以免费了,处理方式是按照长从大到小排序,然后剔除其中宽小于前者的土地,最终得到的土地是长递增、宽递减的。那么转移方程式就可以写成:f[i]=f[j]+l[j+1]*w[i]了,直接斜率优化就行了。。。

#include<bits/stdc++.h> using namespace std; #define ll long long #define N 500005 template <typename dr>void read(dr &a){ dr x=0,f=1;char ch=getchar(); for(;!isdigit(ch);ch=getchar())if(ch==‘-‘)f=-1; for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-‘0‘; a=x*f; } struct ly{ ll w,l; }a[N]; ll dp[N],q[N]; bool cmp(ly a,ly b){ return a.w==b.w ? a.l>b.l : a.w>b.w; } int main() { ll n,m=0; read(n); for(int i=1;i<=n;i++)read(a[i].w),read(a[i].l); sort(a+1,a+1+n,cmp); for(int i=1;i<=n;i++)if(a[m].l<a[i].l)a[++m]=a[i]; int l=1,r=1; //printf("\n"); //for(int i=1;i<=m;i++)printf("%lld %lld\n",a[i].w,a[i].l); for(int i=1;i<=m;i++){ while(l<r&&(dp[q[l+1]]-dp[q[l]])<=a[i].l*(a[q[l]+1].w-a[q[l+1]+1].w))++l; dp[i]=dp[q[l]]+a[q[l]+1].w*a[i].l; //printf("%lld %lld\n",dp[q[l+1]]-dp[q[l]],a[q[l+1]+1].w-a[q[l]+1].w); while(l<r&&(dp[q[r]]-dp[q[r-1]])*(a[q[r]+1].w-a[i+1].w)>=(dp[i]-dp[q[r]])*(a[q[r-1]+1].w-a[q[r]+1].w))--r; q[++r]=i; } printf("%lld\n",dp[m]); return 0; }
洛谷P5504 柠檬
此题较有意思,初看写出转移方程似乎较难计算,前缀和也不能开过大数组浪费空间,但试想一下,转移方程的时候,是不是要i、j的大小相等呢?这很容易想明白,若大小不相等,可以找到相等的地方作为端点拆开来,形成新的一段,岂不美哉,用vector数组进行单调性优化,因为每个点只进来和出去一次,这里求得是最大值,而我们一次函数y=kx+b的斜率是单调递增的,所以要用单调栈维护。

#include<bits/stdc++.h> using namespace std; template<typename dr>void read(dr &a){ dr x=0,f=1;char ch=getchar(); for(;!isdigit(ch);ch=getchar())if(ch==‘-‘)f=-1; for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-‘0‘; a=x*f; } #define ll long long #define ri register int #define Y(i,j) (f[i-1]+a[i]*(s[i]+1)*(s[i]+1)-f[j-1]-a[j]*(s[j]+1)*(s[j]+1)) #define X(i,j) (s[i]-s[j]) #define t1 q[t][q[t].size()-1] #define t2 q[t][q[t].size()-2] const int N=1e6+5; ll f[N],s[N],a[N],last[10005]; inline ll calc(int i,int j){return f[j-1]+a[i]*(s[i]-s[j]+1)*(s[i]-s[j]+1);} vector<int>q[10005]; int main() { ll n,ans=0; read(n); for(ri i=1;i<=n;i++){ read(a[i]); s[i]=s[last[a[i]]]+1;last[a[i]]=i; } for(ri i=1;i<=n;i++){ int t=a[i]; while((q[t].size()>=2)&&Y(t1,t2)*X(i,t1)<=Y(i,t1)*X(t1,t2)){q[t].pop_back();} q[t].push_back(i); while((q[t].size()>=2)&&calc(i,t1)<=calc(i,t2)){q[t].pop_back();} f[i]=calc(i,t1); } printf("%lld\n",f[n]); return 0; }
斜率优化的做题步骤大致可以分为:剔除外壳、写出粗糙的伪方程(建议用类似数学符号∑简略表示一下)、然后简化计算方式(前缀和啊什么的)、移项化为一次函数。
综合上面辣么多的斜率优化题,我们已经会初步优化i、j之间有关联的dp了,但仅限于平方,若是更高的次幂,或是其他奇怪复杂的函数计算呢?
定义:设w(i,j)为整数集合上的二元函数,若对于任意的a,b,c,d,设a<=b<=c<=d,都有w(a,d)+w(b,c)>=w(a,b)+w(b,d),则称w(i,j)满足四边形不等式。
定理1:对于二元函数w(i,j),对于任意a<b,都有w(a,b+1)+(a+1,b)>=w(a,b)+w(a+1,b+1),则函数w满足四边形不等式。
证明:

那么它有什么用呢,emmmmm李煜东大佬的书上讲的非常清楚,这里这个dalao的博客里也有很详细的说明,其次要说的就是,若你求的是max,则四边形不等式的符号取反即可证明其决策单调性。
聪明的大佬已经发现,斜率优化有时候算是决策单调性dp的一部分,所以决策单调性也分单调栈和单调队列,对于计算二元函数复杂的题目要用分治的做法来解决。点我查看详情。
洛谷P1912 诗人小G

你看这是什么诗嘛……brysj,hhrhl。yqqlm,gsycl。怕了你了……
这里先写出状态转移方程:f[i]=Min{f[j]+val(i,j)},记a[i]为第i句诗的长度,sum[i]为前i句的总长度,val(i,j)=|sum[i]-sum[j]+(i-j-1)-L|p。
要证明val(i,j)满足四边形不等式,则要证明val(i,j+1)+val(i+1,j)>=val(i,j)+val(i+1,j+1),移项得val(i,j+1)-val(i+1,j+1)>=val(i,j)-val(i+1,j);
设u=(sum[i]+i)-(sum[j]+j)-(L+1),v=(sum[i]+i)-(sum[j]+j+1)-(L+1),则上式可化为|v|p-|v+a[i+1]+1|p>=|u|p-|u+a[i+1]+1|p,u>v,则我们要证明函数f(u)=|u|p-|u+a[i+1]+1|p单调递减。
这玩意儿求导来证明最好不过了吧,分奇数和偶数两种情况来证明各个取值范围的函数,若导函数f‘(u)始终为负,则函数递减,这里不多做证明,自己想想吧。
什么?!你问我导数是什么,导数就是……引导你解决问题的数,嗯对,就是这样((((
对于决策单调性的DP,转移过程中保证后续状态i‘的转移点不会比i靠前,当求出一个新i的时候,我们应该考虑i可以作为那些后续状态i‘的转移决策点,最终我们会找到一个位置,使得该位置之前的决策在当前lk数组里保存的决策都比i好,该位置之后k的决策都比i差,然后将i放入其中,我们只需要保存这个临界值的位置,若后求得的临界值小于队尾的临界值,则说明队尾无法成为最优决策点,弹掉队尾即可。

#include<bits/stdc++.h> using namespace std; #define ld long double template<typename dr>inline void read(dr &a){ dr x=0,f=1;char ch=getchar(); for(;!isdigit(ch);ch=getchar())if(ch==‘-‘)f=-1; for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-‘0‘; a=x*f; } const int N=1e5+5; ld f[N]; int q[N],k[N],s[N],pr[N],p,L,n; char c[N][32]; #define calc(i,j) f[j]+qpower(fabs(s[i]-s[j]-L)) inline ld qpower(ld b){ ld a=1; for(int x=p;x;x>>=1,b*=b) if(x&1)a*=b; return a; } inline int query(int x,int y){//查询临界值,即--临界值之前由x转移答案较好,之后由y转移答案较好 int l=y,r=n+1; while(l<r){ int mid=l+r>>1; calc(mid,x)>=calc(mid,y)?r=mid:l=mid+1;//计算mid究竟是由x转移好还是由y转移好,找到临界值。 } return l; } int main() { int t; read(t); while(t--){ memset(q,0,sizeof(q)); read(n);read(L);read(p);L++; for(int i=1;i<=n;i++)scanf("%s",c[i]),s[i]=strlen(c[i])+s[i-1]+1; int l=1,r=1; for(int i=1;i<=n;i++){ while(l<r&&k[l]<=i)++l;pr[i]=q[l]; f[i]=calc(i,q[l]); while(l<r&&k[r-1]>=query(q[r],i))--r; k[r]=query(q[r],i);q[++r]=i; } if(f[n]>1e18){ puts("Too hard to arrange"); } else { printf("%.0Lf\n",f[n]); int i; for(q[l=0]=i=n;i;q[++l]=i=pr[i]); for(;l;l--){ for(i=q[l]+1;i<q[l-1];i++) printf("%s ",c[i]); puts(c[i]); } } puts("--------------------"); } return 0; }
P3515 Lightning Conductor

这题的绝对值比较难一带而过,所以烦的一批,不如分成i>j和i<j两部分,循环两边进行计算。

另一种形象的说法,本题的函数增速是递减的,所以被超过的函数这辈子都只能碾压了2333333,这就是传说中的永无出头之日了吗

#include<bits/stdc++.h> using namespace std; #define ri register int const int N=5e5+5; template<typename dr>inline void read(dr &a){ dr x=0,f=1;char ch=getchar(); for(;!isdigit(ch);ch=getchar())if(ch==‘-‘)f=-1; for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-‘0‘; a=x*f; } int a[N],q[N],k[N],n; double f[N],sq[N]; #define calc(i,j) sq[i-j]+a[j] /*inline int query(ri x,ri y){ ri l=y,r=k[x]?k[x]:n,mid;r++; while(l<r){ mid=l+r>>1; calc(mid,l)+a[l]<=calc(mid,r)+a[r]?r=mid:l=mid+1; } return l; }*/ inline int query(ri x,ri y){//二分临界值k ri l=y,r=k[x]?k[x]+1:n+1,m;//控制二分上下界 while(l<r){ m=(l+r)>>1; if(calc(m,x)<=calc(m,y))r=m; else l=m+1; } return r; } void wok(){ ri l=1,r=0; for(ri i=1;i<=n;i++){ while(l<r&&k[l]<=i)++l; f[i]=max(f[i],calc(i,q[l])); while(l<r&&k[r-1]>=query(q[r],i))--r; k[r]=query(q[r],i);q[++r]=i; } } int main() { read(n); for(ri i=1;i<=n;i++)read(a[i]),sq[i]=sqrt(i); wok(); reverse(a+1,a+n+1); reverse(f+1,f+n+1); memset(k,0,sizeof(k)); wok(); for(ri i=n;i>=1;i--){ printf("%d\n",max((int)ceil(f[i])-a[i],0)); } return 0; }
洛谷CF868F Yet Another Minimization Problem
终究还是来了,这题函数计算比较的难,需要递归分治的方法。

#include<bits/stdc++.h> using namespace std; #define R register int #define RG register #define ll long long template<typename dr>void read(dr &a){ dr x=0,f=1;char ch=getchar(); for(;!isdigit(ch);ch=getchar())if(ch==‘-‘)f=-1; for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-‘0‘; a=x*f; } const int N=1e5+5; ll f[N],g[N],c[N],a[N],n,k; ll nl=1,nr,ans; void get(int l,int r){ while(l<nl)ans+=c[a[--nl]]++; while(nr<r)ans+=c[a[++nr]]++; while(nl<l)ans-=--c[a[nl++]]; while(nr>r)ans-=--c[a[nr--]]; } void dp(int l,int r,int kl,int kr){//l,r:区间。kl,kr:决策区间。经处理,最佳决策点不会超过kr,也不会低于kl。 if(l>r)return; int mid=l+r>>1,x=0; for(R i=min(mid,kr+1);i>kl;i--){ get(i,mid); if(g[i-1]+ans<f[mid])f[mid]=g[i-1]+ans,x=i-1;//找到能更新mid的最优决策点,右端不会低于该点,左端不会大于该点。 } dp(l,mid-1,kl,x);dp(mid+1,r,x,kr); } int main() { read(n),read(k);//类比这种分成k段的dp,循环k次就可以压掉一维,滚动数组大法好,真善忍好! for(R i=1;i<=n;i++){ read(a[i]);f[i]=f[i-1]+c[a[i]]++; //printf("%d ",a[i]); } memset(c,0,sizeof(c)); while(--k){ for(int i=1;i<=n;i++)g[i]=f[i],f[i]=1e18; //ans=nr=nl=0; dp(1,n,0,n-1); } printf("%lld\n",f[n]); return 0; }
所以说决策单调性的dp要求本人拥有很强大的数学基础,能够证明出函数是否满足四边形不等式,或者直接证明出其满足决策单调性,顺便理出清晰的dp思路,对数学要求严苛,我这样的蒟蒻只能写个大概,提高组应该不会考吧,于是乎我也只是浅尝辄止,希望以后还能有机会来复习2333333。
那么序列类的DP就到此为止了,断断续续每天抽时间写了7天。唉,不断前行在孤独与人的丑恶之中,悲哀里透着的是平淡,愿被苦海洗涤之人梦终入海,祭oi路上的你我秋风不再。
标签:mat log max 滑动 转移 思考 family 简单的 滚动
原文地址:https://www.cnblogs.com/zxrswill/p/13276144.html