ESN简介

标签：alpha   必须   details   简单的   sns   输入   最大   空间   相互   

0. 前言

通常神经网络的问题：

• 参数如何选择
• 何时停止训练
• 局部最优解

1. 回声网络ESN

具有以下特点：

• 大且稀疏生物连接，RNN被当做一个动态水库
• 动态水库可以由输入或/和输出的反馈激活
• 水库的连接权值不会被训练改变？
• 只有水库的输出单元的权值随训练改变，因此训练是一个线性回归任务

假设有ESN是一个可调谐的sin波生成器：

• 黑色箭头是指固定的输入和反馈连接
• 红色箭头指可训练的输出连接
• 灰色表示循环内连接的动态水库

典型RNN存在的问题：

• 没有明确的终止条件
• 通常这些算法收敛速度慢和/或导致次优解
• ESN使用大循环水库（50-1000），而RNN通常只用到5-30个神经元

为什么需要循环神经网络：

• 如果人们想要模拟、预测、过滤、分类或控制非线性动力系统，就需要一个可执行的系统模型
• 通常获得分析模型是不可行的，因此必须使用黑箱建模技术
• 对于线性系统，可以使用有效的黑箱建模方法
• RNNs可用于非线性动力系统的建模

为什么使用ESN：

• 统计信号处理的典型方法是建立在三个基本假设：线性、稳定和高斯分布。为了便于数学计算而引入的假设。

• 大多数的实际物理信号是由动态过程产生，这些过程是非线性的、非稳定的和非高斯的

• ESNs和一般RNNs在非线性领域推广了简单的自适应线性滤波器，可用于任何非线性动力系统的建模

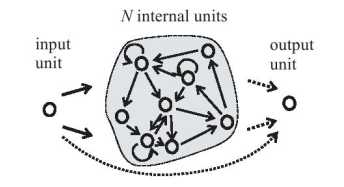
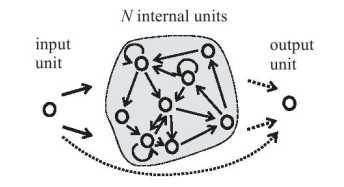
输入到水库是全连接，水库到输出是全连接，水库内部不是全连接

ESN描述：

• 水库有N个内部网络单元
• 在时刻\(n \geq 1\)，输入是\(u(n)\)，输出是\(y(n)\)
• 内部单元的激活是一个\(N*1\)向量：\(x(n)=(x_1(n), ...,x_N(n))\)
• 水库内部连接表示为一个\(N*N\)的矩阵\(W\)，表示内部的拓扑结构以及连接的权值
• 输入权值表示为\(N*1\)的向量\(w^{in}\)
• 输出权值表示为\((N+1)*1\)的向量\(w^{out}\)
  • 因为有水库输出权值连接\(N\)，以及输入到输出的连接\(1\)，所以为\((N+1)\)长度的向量

非线性系统描述：

• \(x(n+1)=f(Wx(n)+w^{in}u(n+1)+v(n+1))\)

  • 每个神经元都和输入、部分神经元连接，

• \(y(n+1)=f^{out}(w^{out}(u(n+1),x(n+1)))\)

（内部状态\(x(n)\)指的是什么？）

在确定条件下网络状态逐渐独立于初始状态，并只依赖于输入历史，体现网络的记忆能力：

• \(W\)有谱半径\(|\lambda_{max}|>1\)，谱半径是矩阵的最大特征值，此时就会丢失回声特性，需要对其做归一化处理，\(W_{new}=W/|\lambda_{max}|\)

  • 为了保证系统稳定能够收敛，需要将\(Wx=y\)的输出\(y\)小于输入\(x\)，\(W_{new}=W/|\lambda_{max}|\)
  • 特征值的概念就是方阵在特征向量上的投影，特征向量相当于是空间中的一组基，所以特征值相当于是方阵在一组基上的半径。谱半径是这种半径的最大值，也就是最大特征值。除以\(\lambda_{max}\)相当于归一化。

• \(W\)最好是稀疏矩阵

• 通常\(W\)是由\([-1,1]\)的均匀分布随机生成，然后使用\(|\lambda_{max}|\)做归一化处理使谱半径\(\alpha\)小于1，\(\alpha\)是ESN成功的重要参数，小的\(\alpha\)对应快的信号，大的\(\alpha\)对应慢信号和更长的短时记忆。

在训练时我们计算输出权值，误差描述为：

\(e_{train}(n) = (f^{out})^{-1}y_{teach}(n)-w^{out}(u_{teach}(n),x(n))\)

离线训练算法过程：

• 初始化\(W\)，保证其谱半径\(\alpha<1\)，用输入的教师信号运行ESN
• 从初始瞬态中消除数据，并将剩余的输入和网络状态\((u_{teach}(n);x_{teach}(n))\)按行收集到矩阵\(M\)中
• 收集训练信号\((f^{out})^{-1}y_{teach}(n)\)到向量\(r\)
• \(w^{out}=(M^{-1}r)^T\)
  • 实质上是求解\(y(n+1)=f^{out}(w^{out}(u(n+1),x(n+1)))\)
  • 假设\(y(n)=w^{out}(u(n), x(n))\)，并且\(U(t) = (u(t), x(t))\)，则有\(w^{out}=y(n)U^T(t)(U(t)U^T(t)-\lambda I)^{-1}\)

由此，就得到了输出权值

ESN将非线性问题转换为线性回归问题，只需要训练输出系数\(w^{out}\)。

4个决定性能的参数：

• 池谱半径，\(\lambda_{max}<1\)是网络稳定的必要条件
• 池规模（节点数），池规模越大对动态系统的描述越接近，但是会带来过拟合
• 池输入单元尺度\(w_{in}\)，需要处理的对象的非线性越强该值越大
• 池稀疏程度，表示池中神经元之间的连接情况，池中不是所有的神经元都存在连接。稀疏程度指的是池中相互连接的神经元占总的神经元的百分比，其值越大非线性能力越强

参考资料：
[1] ESN介绍

ESN简介

标签：alpha   必须   details   简单的   sns   输入   最大   空间   相互   

原文地址：https://www.cnblogs.com/oneflyleader/p/13284142.html