标签:== inf 完成 操作 不可 技术 执行 turn int
本章学习了排序这一操作,排序方法分为两大类:
内部排序:不需要访问外存,分为插入类、交换类、选择类、归并类(2-路归并排序)和分配类(基数排序)。
外部排序:不可能在内存中完成。
(一)插入排序
1、直接插入排序----稳定排序,更适合于初始记录基本有序(正序)的情况
1 void InsertSort(SqList &L) 2 { 3 for(i=2; i<L.length; ++i) 4 if(L.r[i].key<L.r[i-1].key) 5 { 6 L.r[0]=L.r[i]; 7 L.r[i]=L.r[i-1]; 8 for(j=i-2; L.r[0].key<L.r[j].key; --j) 9 L.r[j+1]=L.r[j]; 10 L.r[j+1]=L.r[0]; 11 } 12 }
时间复杂度为O(n²),空间复杂度为O(1)。
2、折半插入排序----稳定排序,只能用于顺序结构,适合初始记录无序、n较大的情况
1 void BiInsertSort(SqList &L) 2 { 3 for(i=2; i<=L.length; ++i) 4 { 5 L.r[0]=L.r[i]; 6 low=l; high=i-1; 7 while(low<=high) 8 { 9 m=(low+high)/2; 10 if(L.r[0].key<L.r[m].key) high=m-1; 11 else low=m+l; 12 } //while 13 for(j=i-l;j>=high+l; --j) 14 L.r[j+l]=L.r[j]; 15 L.r[high+l]=L.r[0]; 16 } 17 }
时间复杂度为O(n²),空间复杂度为O(1)。
3、希尔排序----不稳定排序,只能用于顺序结构,最后一个增量值必须等于1,适合初始记录无序、n较大时的情况
1 void ShellInsert(SqList &L, int dk) 2 {//对顺序表L做一趟增量是dk的希尔插入排序 3 for(i=dk+l; i<=L.length; ++i) 4 if(L.r[i].key<L.r[i-dk].key) 5 { 6 L.r[0]=L.r[i]; 7 for(j=i-dk; j>0 && L.r[0].key<L.r[j].key; j-=dk) 8 L.r[j+dk]=L.r[j]; 9 L.r[j+dk]=L.r[0]; 10 } 11 } 12 void ShellSort(SqList &L, int dt[], int t) 13 { 14 for (k=0; k<t; ++k) 15 ShellInsert(L, dt[k]); 16 }
时间复杂度为O(n3/2),空间复杂度为O(1)。
(二)交换排序
1、冒泡排序----稳定排序,算法平均性能比直接插入排序差
1 void BubbleSort(SqList &L) 2 { 3 m=L.length-1; flag=1; //flag用来标记某一趟排序是否发生交换 4 while((m>0)&&(flag==1)) 5 { 6 flag=0; //flag置0,如果本趟排序没有发生交换,则不会执行下一趟排序 7 for(j=1; j<=m; j++) 8 if(L.r[j].key>L.r[j+1].key) 9 { 10 flag=1; //flag置为1,表示本趟排序发生了交换 11 t=L.r[j]; L.r[j]=L.r[j+1]; L.r[j+1]=t;//交换 12 } 13 --m; 14 } 15 }
时间复杂度为O(n²),空间复杂度为O(1)。
2、快速排序----不稳定排序,适合用于顺序结构,适合初始记录无序、n较大时的情况
1 int Partition(SqList &L, int low, int high) 2 {//对顺序表1中的子表r[low .. high)进行一趟排序,返回枢轴位置 3 L.r[0]=L.r[low]; 4 pivotkey=L.r[low].key; //枢轴记录关键字保存在pivotkey中 5 while(low<high) 6 { 7 while(low<high && L.r[high].key>=pivotkey) --high; 8 L.r[low]=L.r[high]; //将比枢轴记录小的记录移到低端 9 while(low<high && L.r[low].key<=pivotkey) ++low; 10 L.r[high]=L.r[low]; //将比枢轴记录大的记录移到高端 11 } 12 L.r[low]=L.r[0]; 13 return low; 14 } 15 void QSort(SqList &L, int low, int high) 16 { 17 if(low<high) 18 { 19 pivotloc=Partition(L, low, high); 20 QSort(L, low, pivotloc-1); //对左子表递归排序 21 QSort(L, pivotloc+l, high); //对右子表递归排序 22 } 23 } 24 void QuickSort(SqList &L) 25 { 26 QSort(L, 1, L.length); 27 }
平均情况下,快速排序的时间复杂度为O(nlog2n)。
最好情况下的空间复杂度为O(log2n)--递归要用到栈空间,最坏情况下为O(n)。
(三)选择排序
1、简单选择排序/直接选择排序----稳定排序,比直接插入排序快
1 void SelectSort(SqList &L) 2 { 3 for(i=1; i<L.length; ++i) 4 { 5 k=i; 6 for(j=i+l; j<=L.length; ++j) 7 if(L.r[j].key<L.r[k].key) k=j; 8 if(k!=i) 9 {t=L.r[i; L.r[i]=L.r[k]; L.r[k]=t;} 10 }//for 11 }
时间复杂度为O(n²),空间复杂度为O(1)。
2、树形选择排序/锦标赛排序
3、堆排序----不稳定排序,只能用于顺序排序
1 //1.调整堆----筛选法 2 void HeapAdjust(SqList &L, int s, int m) 3 { 4 rc=L.r[s]; 5 for(j=2*s; j<m; j*=2) 6 { 7 if(j<m && L.r[j].key<L.r[j+1].key) ++j; 8 if(rc.key>=L.r[j].key) break; 9 L.r[s]=L.r[j]; s=j; 10 } 11 L.r[s]=rc; 12 } 13 //2.初建堆 14 void CreatHeap(SqList &L) 15 {//把无序序列L.r[l..n]建成大根堆 16 n=L.length; 17 for(i=n/2;i>O; --i) 18 HeapAdjust(L,i,n); 19 } 20 //3.堆排序算法的实现 21 void HeapSort(SqList &L) 22 { 23 CreatHeap(L); 24 for(i=L.length; i>l; --i) 25 { 26 x=L.r[1]; 27 L.r[1]=L.r[i]; 28 L.r[i]=x; 29 HeapAdjust(L, 1, i-1) 30 } 31 }
堆排序在最坏的情况下,其时间复杂度也为O(nlog2n),空间复杂度为O(1)。
实验研究表明,平均性能接近于最坏性能。
(五)归并排序----稳定排序
1 void MSort(RedType R[], RedType &T[], int low, int high) 2 { 3 if(low==high) T[low]=R[low]; 4 else 5 { 6 mid=(low+high)/2; 7 MSort(R, S, low, mid); 8 MSort(R, S, mid+l, high); 9 Merge(S, T, low, mid, high); 10 } 11 } 12 void MergeSort(SqList &L) 13 { 14 MSort(L.r, L.r, 1, L.length); 15 }
时间复杂度为O(nlog2n),空间复杂度为O(n)。
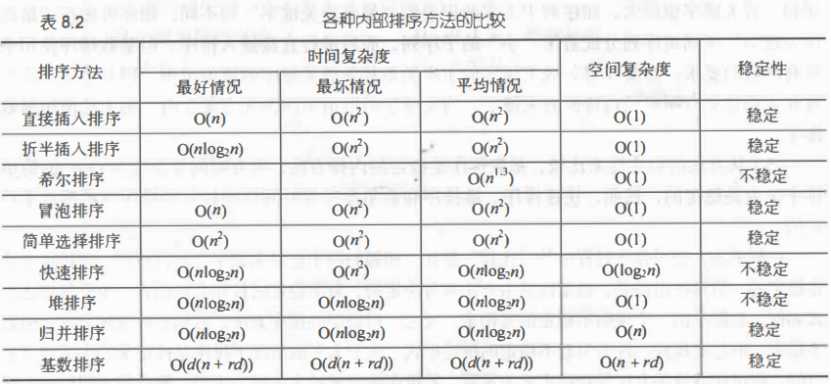
各种内部排序方法的比较:
标签:== inf 完成 操作 不可 技术 执行 turn int
原文地址:https://www.cnblogs.com/zzssx/p/13289268.html