标签:lazy color lsp 解决 方法 交换 元素 ceil lang
一、算法分析
(一)时间效率——排序速度(比较 & 移动)
(二)空间效率——占内存辅助空间大小
(三)稳定性——A和B关键字相等,排序后先后次序保持不变
二、内部排序:不需要访问外存
(一)插入排序(每一趟:查找位置——记录后移——插入位置)
1、直接插入排序(顺序查找)
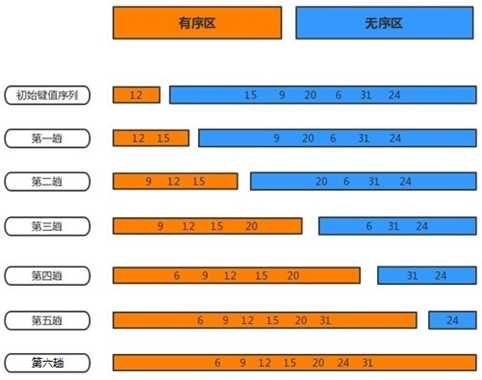
(1)思想:依次将待排序列中的记录插入到一个已排序列中,直到全部记录都有序。
(2)分析:设对象个数为n,则执行n-1趟
|
第i趟 |
最好(初始排列有序) |
最坏(初始排列逆序) |
|
比较次数 |
n-1 |
i |
|
移动次数 |
1 |
i+1 |
时间复杂度:O(n)
空间复杂度:O(1)
2、折半插入排序(折半查找)
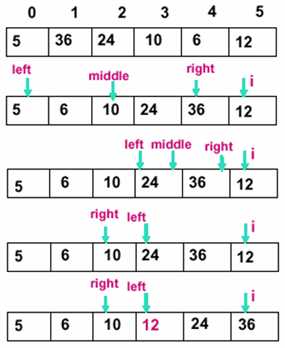
(1)思想:先取已排序列的中间元素,与待插入数据进行比较,如果中间元素的值大于待插入数据,那么待插入数据属于数组前半部分,否则属于后半部分。依次类推,不断缩小范围,确定插入位置。
(2)分析:比较次数与初始排列无关,仅依赖于对象个数;移动次数与直接插入排序相同,依赖于对象的初始排列。(减少了比较次数,但没有减少移动次数;平均性能优于直接插入排序)
- 在插入第 i 个对象时,需要经过 ⌊log2i⌋ +1 次关键码比较,才能确定它应插入的位置。
- 当 n 较大时,总关键码比较次数比直接插入排序的最坏情况要好得多,但比其最好情况要差。
- 在对象的初始排列已经按关键码排好序或接近有序时,直接插入排序比折半插入排序执行的关键码比较次数要少。
时间复杂度:O(n2)
空间复杂度:O(1)
3、希尔排序(缩小增量)
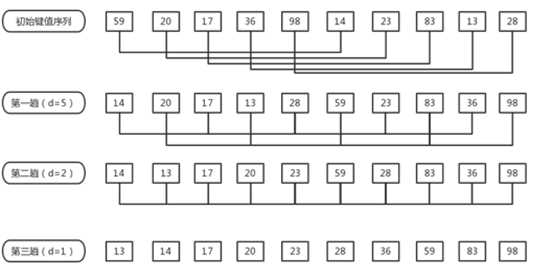
(1)思想:将序列按下标的一定增量分组,对每组使用直接插入排序,当增量减至1时,整个序列恰好被分为一组,排序终止。
(2)分析:最佳d序列尚未解决,永远不要使用2的幂次量作为增量,推荐9,5,3,1;
时间复杂度是n和d的函数, O(n1.25) ~ O(1.6*n1.25);
空间复杂度为O(1)。
(二)交换排序(两两比较,前小后大,逆序交换)
1、冒泡排序
(1)分析:设对象个数为n
|
第i趟 |
最好(初始排列有序) |
最坏(初始排列逆序) |
|
排序次数 |
1 |
n-1 |
|
比较次数 |
n-1 |
n-i |
|
移动次数 |
0 |
3*(n-i) |
时间复杂度:O(n2)
空间复杂度:O(1)
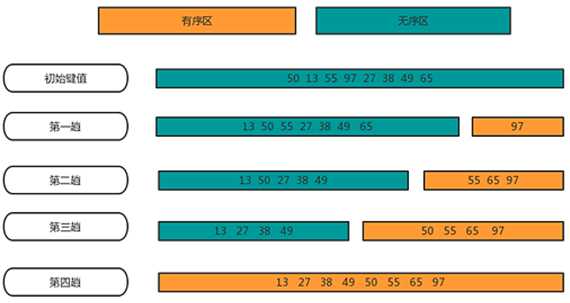
2、快速排序(分区交换排序)
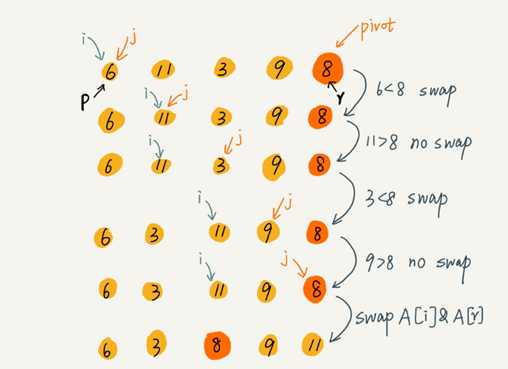
(1)改进:
a.冒泡排序:记录的比较和移动是在相邻位置进行的,记录每次交换只能后移一个位置,因而总的比较次数和移动次数较多。
b.快速排序:记录的比较和移动是从两端向中间进行的,关键码较大的记录一次就能从前面移动到后面,关键码较小的记录一次就能从后面移动到前面,记录移动的距离较远,从而减少了总的比较次数和移动次数。
(2)思想:选取一个枢轴,将待排序记录划分为二,左侧记录的关键码均小于或等于轴值,右侧记录的关键码均大于或等于轴值,然后分别对这两部分重复上述过程,直到整个序列有序。
(3)分析:快速排序是递归的,需要有一个栈存放每层递归调用时参数(新的low和high)。最大递归调用层次数与递归树的深度一致,因此,要求存储开销为 O(log2n)。
|
|
最好(划分后左右侧同长) |
最坏(初始排列有序) |
|
时间复杂度 |
O(nlog2n) |
O(n2) |
|
空间复杂度 |
O(nlog2n) |
|
(三)选择排序
1、简单选择排序
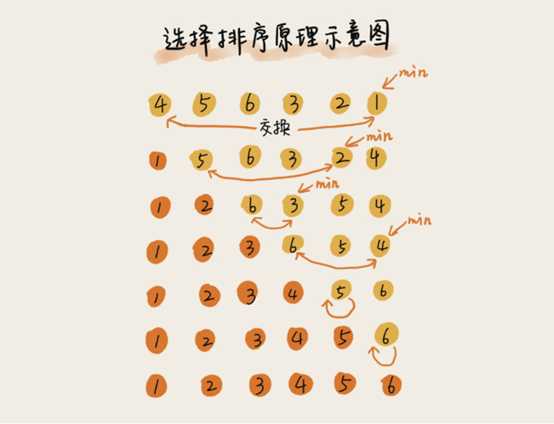
(1)思想:每次从待排序列中找到最小的元素,将其放到已排序列的末尾。
(2)分析:
|
第i趟 |
最好(初始排列有序) |
最坏(初始排列逆序) |
|
排序次数 |
1 |
n-1 |
|
比较次数 |
n-1 |
n-i |
|
移动次数 |
0 |
3*(n-i) |
2、堆排序
适用于n较大的情况
(1)堆:
n个元素的序列[k1: kn]是堆,当且仅当
如果将序列看成一棵完全二叉树,非终端结点的值均小于或大于左右结点的值。
(2)思想:将无序序列建堆,输出堆顶的最小(大)值,使剩余的n-1个元素重新调整成一个堆,则可得到n个元素的次小值,重复执行,得到一个有序序列。
(四)归并排序
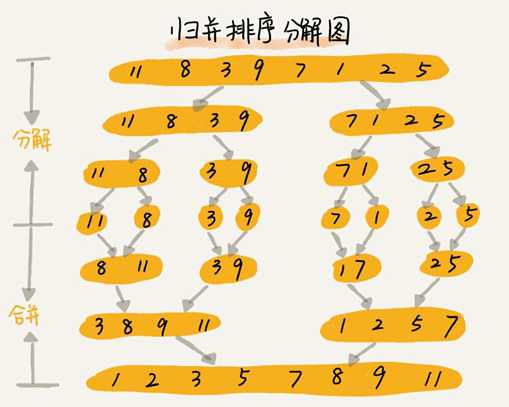
(1)思想:分治策略,将待排元素均分两组,如不易解决,则继续分解,直至子序列中包含一个元素,然后自底向上合并得到一个有序序列。
(2)分析:设n个对象,则共需进行⌈log2n⌉趟,时间复杂度为O(nlogn);归并需要辅助数组T,则空间复杂度O(n)
三、算法效率总结
|
排序方法 |
时间性能 |
空间性能 |
稳定性能 |
备注 |
||
|
最好 |
最坏 |
平均 |
||||
|
直接插入排序 |
O(n) |
O(n^2) |
O(n^2) |
O(1) |
? |
|
|
折半插入排序 |
O(nlogn) |
O(n^2) |
O(n^2) |
O(1) |
? |
|
|
希尔排序 |
|
|
O(n^1.3) |
O(1) |
? |
|
|
冒泡排序 |
O(n) |
O(n^2) |
O(n^2) |
O(1) |
? |
|
|
快速排序 |
O(nlogn) |
O(n^2) |
O(nlogn) |
O(logn) |
? |
1)就平均计算时间而言,快排是所讨论的内排序方法中最好的; 2)初始排列有序时,快排序蜕化为冒泡排序 |
|
简单选择排序 |
O(n^2) |
O(n^2) |
O(n^2) |
O(1) |
? |
三者的时间性能不随记录序列中关键字分布而改变 |
|
堆排序 |
O(nlogn) |
O(nlogn) |
O(nlogn) |
O(1) |
? |
|
|
归并排序 |
O(nlogn) |
O(nlogn) |
O(nlogn) |
O(n) |
? |
|
|
基数排序 |
O(d(n+rd)) |
O(d(n+rd)) |
O(d(n+rd)) |
O(n+rd) |
? |
外部排序 |
标签:lazy color lsp 解决 方法 交换 元素 ceil lang
原文地址:https://www.cnblogs.com/originaldoll/p/13287953.html