标签:bsp 字母 com ios 存在 字符 地方 code 查找


Trie树的定义

适用于Trie树的题目的特点:
这些字符串要么都是小写字母,要么都是大写字母,要么就是数字,要么就是0和1
反正就是类型很少
首先trie树是有一个根节点
然后我们在存的时候在每个单词结尾的地方打一个标记,表示以这个字符结尾的节点,是有一个字符串的
假设现在需要存储这么多字符串的话,Trie树就长这样
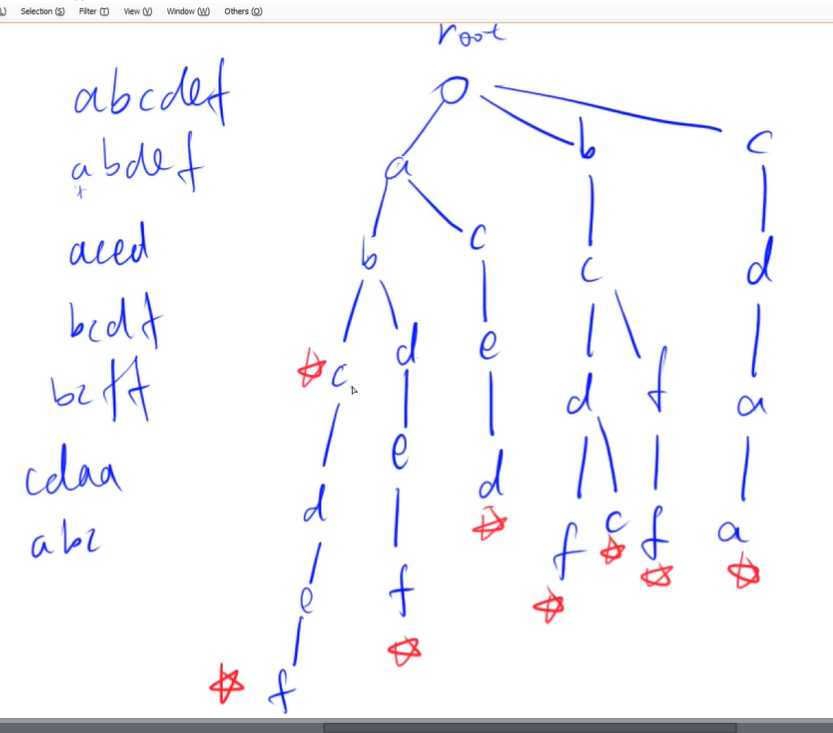
上面这是Trie树的存储
然后看Trie树的查找
Trie树可以高效的查找一个字符串在整个集合中是否出现过,以及出现了多少次
比如现在想查找aced这个串
从根节点走
走到d的时候,这个单词已经遍历完了,而且d上有一个标记
那就说明在这个集合当中,存在一个aced
比如查找abcf,字母f不存在,就说明这个串不存在
比如查找abcd,各个字母虽然存在,但是d上没有标记,就说明这个串不存在
比如说有个点下标是x
那么x这个节点的所有儿子的话,就存在了son[x][]里
那么son[x][0]存储的就是x的第0个儿子
只有根节点的话,idx = 0
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int N = 100010; //最多N个字母,节点个数最多为N 4 int son[N][26]; //因为只包含小写英文字母,每个节点最多向下连26条边,每个节点的子节点个数最多为26 5 //son数组存储每个点的所有儿子 6 int cnt[N]; //以当前这个点结尾的单词有多少个 7 int idx; //同单链表的idx,当前用到了哪个下标 8 //下标是0的点既是根节点又是空节点 9 //如果一个点没有子节点,也把其指向0 10 char str[N]; 11 //存储,也就是插入操作的实现函数 12 void insert(char str[]) { 13 int p = 0; //从根节点开始 14 int len = strlen(str); 15 for (int i = 0; i < len; i++) { //遍历要存储的字符串 16 int u = str[i] - ‘a‘; //把当前这个字母对应的子节点编号计算出来 17 //也就是把a ~ z,映射成0 ~ 25 18 //如果当前这个点上不存在这个字母的话 ,把它创建出来 19 if (!son[p][u]) { //如果p节点不存在u这个儿子的话 20 son[p][u] = ++idx; //创建出来 21 } 22 p = son[p][u]; //走到下一个点 23 //上面三行代码的意思就是说,没有这个节点的话,我创造一个节点,也要走到这个节点上去 24 //有这个节点的话,我就走到这个节点上去 25 //最后p就走到插入单词最后一个点 26 } 27 cnt[p]++; //以这个点结尾的单词数量加一 28 } 29 //查询操作,返回字符串出现多少次 30 int query(char str[]) { 31 int p = 0; 32 for (int i = 0; str[i]; i++) { 33 int u = str[i] - ‘a‘; 34 if (!son[p][u]) { 35 return 0; 36 } 37 p = son[p][u]; 38 } 39 return cnt[p]; 40 } 41 int main() { 42 ios::sync_with_stdio(false); 43 cin.tie(0); 44 int n; 45 cin >> n; 46 while (n--) { 47 string op; 48 cin >> op; 49 cin >> str; 50 if (op == "I") { 51 insert(str); 52 } else { 53 cout << query(str) << endl; 54 } 55 } 56 return 0; 57 }
标签:bsp 字母 com ios 存在 字符 地方 code 查找
原文地址:https://www.cnblogs.com/fx1998/p/13290768.html