标签：int   初始化   边框   实现   class   toc   problem   想法   任务   

[USACO3.1]形成的区域（P6432）

日期：2020-05-31

一、题意分析

题目链接

1. 任务：给出一张宽为\(A\)长为\(B\)的白纸（颜色为\(1\)），现要求将\(N\)个有颜色且不透明的长方形顺序放在白纸上，可能重叠。求放好后那张纸上呈现的每种颜色的面积。
2. 输入：第一行三个正整数\(A \ B \ N\)，分别表示白纸的长、白纸的宽、长方形的个数；第\(2\)到\(N+1\)行，每行五个整数\(llx \ lly \ urx \ ury \ color\)，表示有一个左下角坐标为\((llx,lly)\)、右上角坐标为\((urx,ury)\)、颜色为\(color\)的长方形。
3. 输出：放好长方形后，输出且只输出那张纸上可视颜色的汇总。每行输出两个正整数，该可视颜色和其总可视面积。输出时按照\(color\)升序输出。
4. 数据范围（原题）：\(1 \leq N \leq 10^3\)，\(1 \leq A, B \leq 10^4\)，\(1 \leq color \leq 2.5 \times 10^3\)。

二、算法分析

1. 暴力

我们知道，暴力的时间复杂度为\(O(A·B·N)\)，即\(10^{11}\)，故无法\(AC\)。

所以，我们在\(Excel\)上枚举暴力的过程，看看能否有所发现。

0). 初始状态（红点为原点）

1). 放第一个长方形

2). 放第二个长方形

3). 放第三个长方形

4). 验证（用\(COUNTIF\)函数）

画图后，我们发现：其实填了大片相同的数字（颜色），如果我们只用一个数字来表示这个区域（小长方形）的话，那就会快很多。

2. 离散化

1). 扫描线

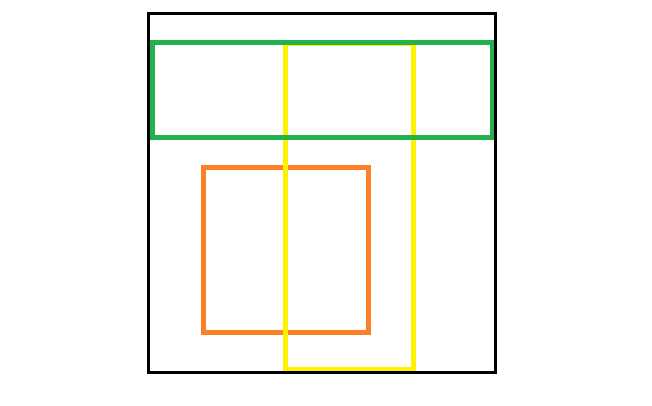
根据上面的想法，我们来绘制这三个长方形和黑色边框的白纸的扫描线。扫描线就是长方形的四边所在的直线（重叠的只画一条，因为有且只有一条）：

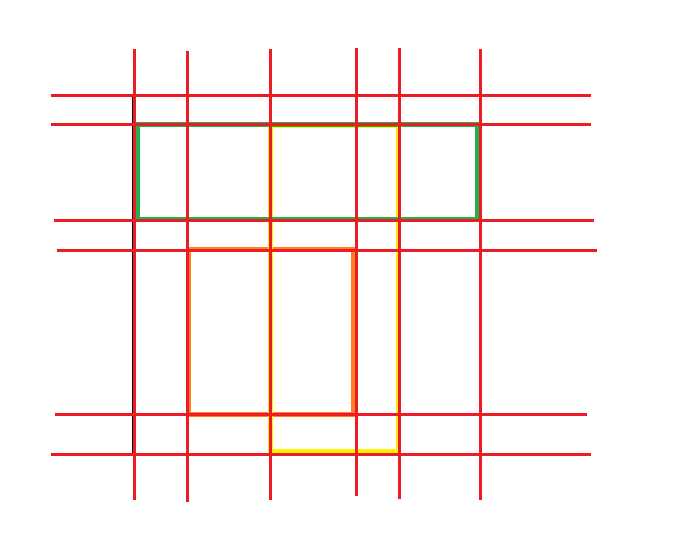
那么，扫描线将这张白纸分为若干个长方形。我们只需要在处理每个长方形时，对涉及到的小长方形填上一个数字（代表一种颜色）即可，而非将每一个面积为\(1\)的最小单位填色。

2). 实现

初始化

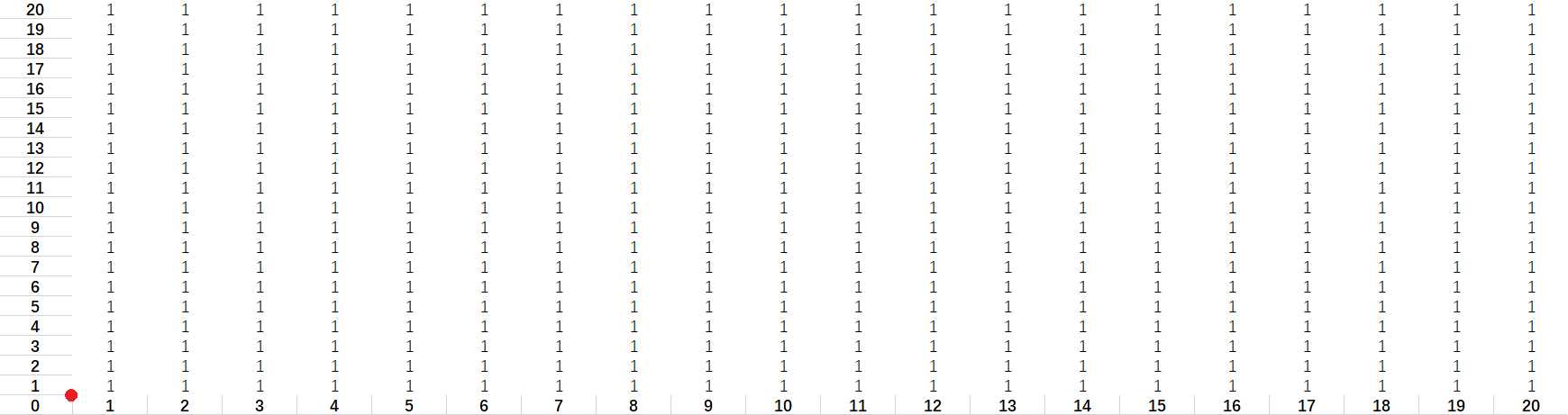
扫描完毕后，将这张纸被切割成的每个小长方形填上\(1\)，表示现在是一张白纸：

放第一个长方形

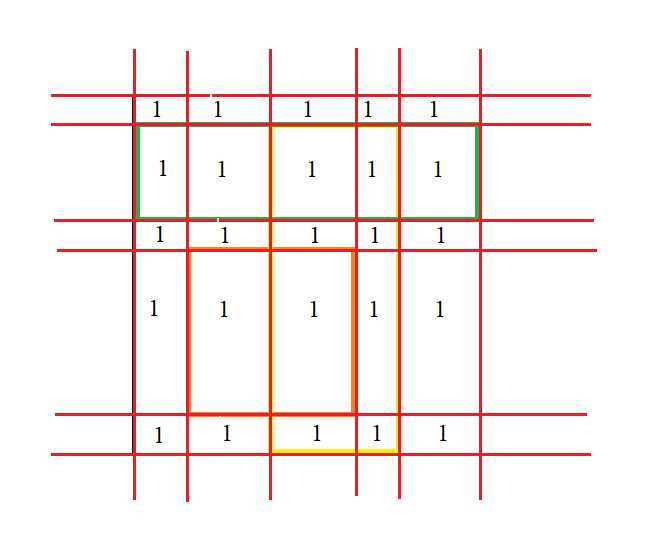
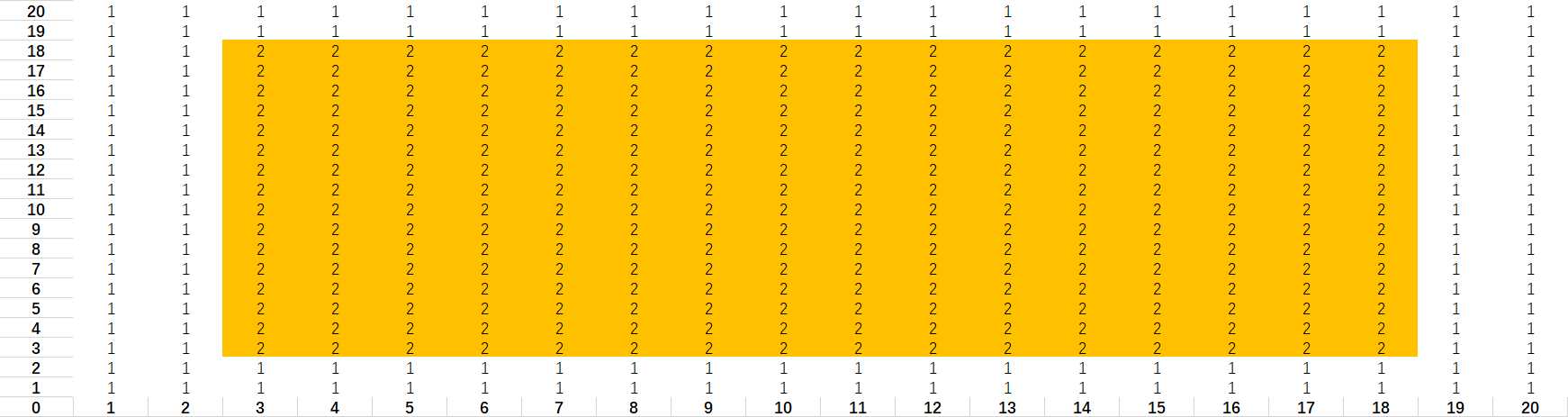
将第一个长方形涉及到的小长方形填上一个数字：

放第二个长方形

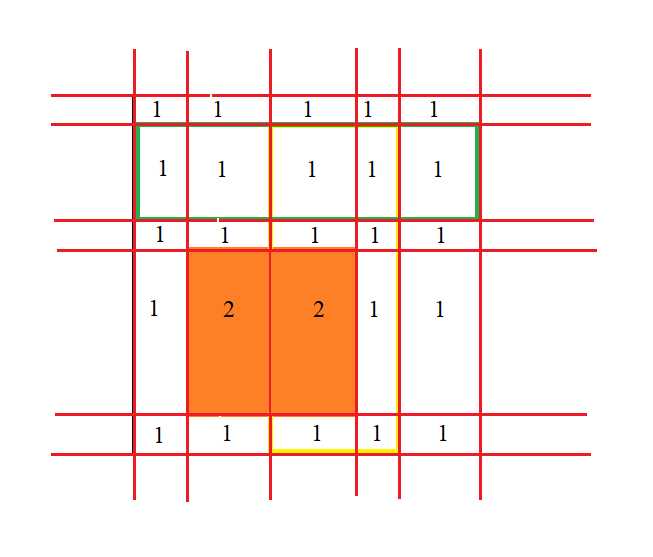
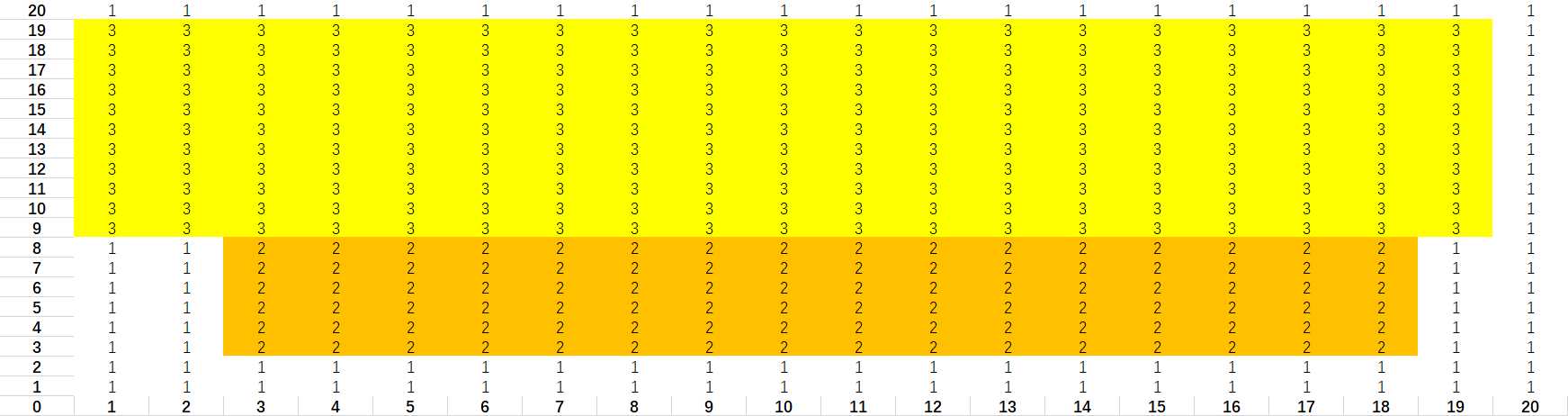
将第二个长方形涉及到的小长方形填上一个数字：

放第三个长方形

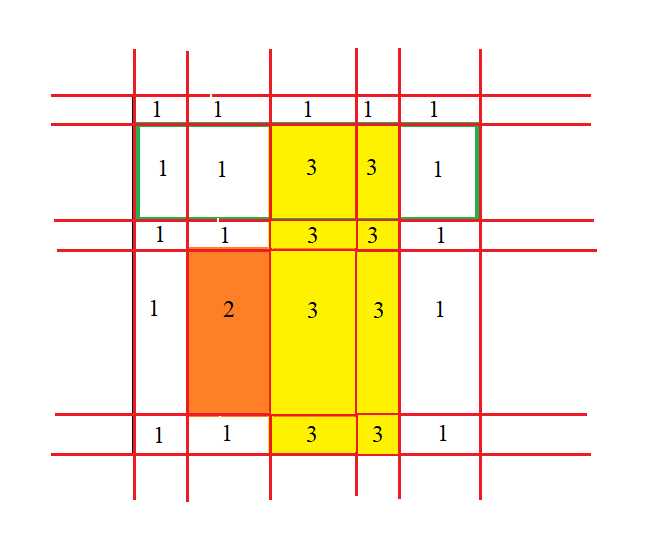
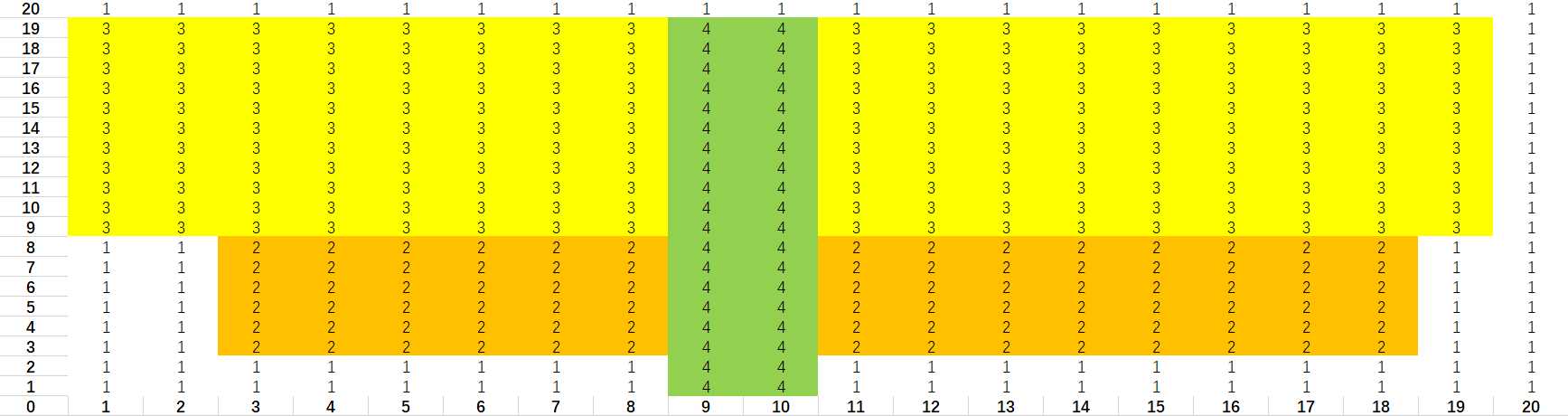
将第三个长方形涉及到的小长方形填上一个数字：

统计

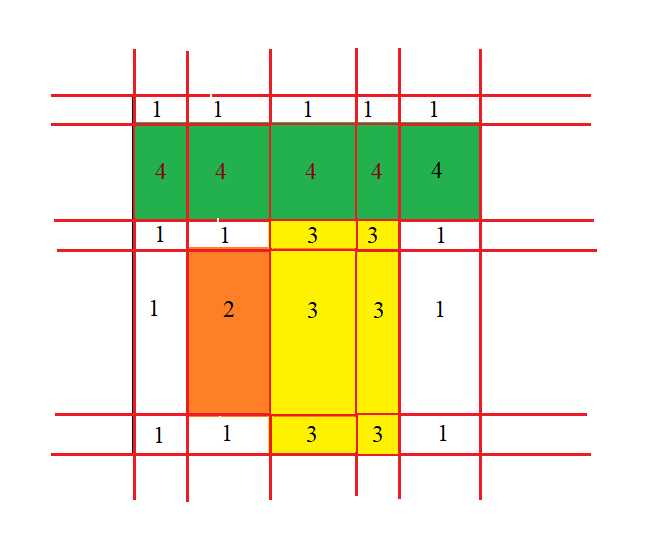
一个可视颜色的总面积，就相当于所有和其颜色（数字）相等的被分割的小长方形的面积和。

三、程序框架

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 1100;
const int N2 = 2200;
const int C = 2750;
const int AB = 11000;

struct node{
	int llx, lly, urx, ury, color;
};
node data[N]; //data存储每个长方形的信息
int map[N2][N2]; //map存储被分割（扫描）后的纸
//linex和liney存储扫描线
//rflcx和rflcy存储映射，即长方形的原始线对应的扫描线编号
//ans[i]表示第i号颜色的总可视面积
int linex[N2], liney[N2], rflcx[AB], rflcy[AB], ans[C]; 
int a, b, n, numx, numy, maxc;

int main(){ 
    //读入
	scanf("%d%d%d", &a, &b, &n);
    
	//读入长方形 然后做扫描线
	numx = numy = 0; maxc = 1;
	for (int i = 1; i <= n; ++i) { 
		scanf("%d%d%d%d%d", &data[i].llx, &data[i].lly, &data[i].urx, &data[i].ury,&data[i].color);
		
		linex[++numx] = data[i].llx;
		linex[++numx] = data[i].urx;
		liney[++numy] = data[i].lly;
		liney[++numy] = data[i].ury;
		
		if (maxc < data[i].color) maxc = data[i].color; //求最大颜色编号
	} 
	
    //处理边界（白纸的）扫描线
	linex[++numx] = 0;
	linex[++numx] = a;
	liney[++numy] = 0;
	liney[++numy] = b;
	
    //排序
	sort(linex + 1, linex + numx + 1);
	sort(liney + 1, liney + numy + 1);
	
    //去重
	int tmp = numx; numx = 1;
	for(int i = 2; i <= tmp; ++i) 
		if (linex[i] != linex[numx]) linex[++numx] = linex[i];
	
	tmp = numy; numy = 1;
	for(int i = 2; i <= tmp; ++i) 
		if (liney[i] != liney[numy]) liney[++numy] = liney[i];
	
    //做映射
	for (int i = 1; i <= numx; ++i) rflcx[linex[i]] = i;
	for (int i = 1; i <= numy; ++i) rflcy[liney[i]] = i;
	
    //初始化：全部赋值为1，表示白纸
	for (int i = 1; i < numx; ++i) 
		for (int j = 1; j < numy; ++j) map[i][j] = 1;
	
    //用长方形不断进行填色
	for (int k = 1; k <= n; ++k) 
		for (int i = rflcx[data[k].llx]; i < rflcx[data[k].urx]; ++i)
			for (int j = rflcy[data[k].lly]; j < rflcy[data[k].ury]; ++j) map[i][j] = data[k].color;
	
    //统计可视颜色面积
	memset(ans, 0, sizeof ans);
	for (int i = 1; i < numx; ++i)
		for (int j = 1; j < numy; ++j) ans[map[i][j]] += (linex[i + 1] - linex[i]) * (liney[j + 1] - liney[j]);
	
    //输出答案
	for (int i = 1; i <= maxc; ++i) 
		if (ans[i] > 0) printf("%d %d\n", i, ans[i]);
	
	return 0;
}  

[USACO3.1.4]形成的区域（P6432）

标签：int   初始化   边框   实现   class   toc   problem   想法   任务   

原文地址：https://www.cnblogs.com/Young06/p/USACO3-1.html