标签:bsp 绿色 没有 变量 校正 加法 element 如何使用 nbsp
色彩(颜色)空间原理(中)
现在我们知道如何定义RGB颜色空间,以及如何使用伽玛曲线在线性和伽玛校正值之间进行转换。剩下的最后一步是将线性RGB颜色转换为XYZ颜色。一旦进入XYZ空间,我们就可以转换回我们选择的任何RGB空间,但这实际上只是开始。因为XYZ空间是定义其他颜色的标准颜色空间,所以我们可以选择转换为许多非RGB颜色空间,例如在感知上更统一的Lab颜色空间或生物驱动的LMS颜色空间。
线性RGB空间和XYZ空间之间转换的基本部分是认识到它们都是矢量空间。这基本上意味着数字以线性方式缩放。相反,经伽玛校正的sRGB空间以非线性方式缩放亮度,因此不是亮度的矢量空间。如果您有某种数学迷信并且想更深入地研究该主题,请查阅 格拉斯曼定律,该定律将色彩感知视为线性组合。
知道我们在向量空间内工作时,便可以使用各种线性代数工具。我们将使用的线性代数中的一种这样的工具是根据另一种颜色空间定义一种颜色空间的基础。这类似于在3d空间中定义对象的变换。
正如我们前面所讨论的,RGB颜色空间是通过将三种原色相加而建立的。第一个原色靠近光谱的红色部分。第二个接近绿色。第三个接近蓝色。为了获得黄色,我们将红色和绿色原色相加。此操作可以视为3维矢量加法。让向量一世一世, ?? 和 ?? 分别等于我们的原色红色,绿色和蓝色,这样

看来我们已经使局势复杂化了,但它会有所收获。首先,让我们来看一些以这种方式定义颜色的示例。
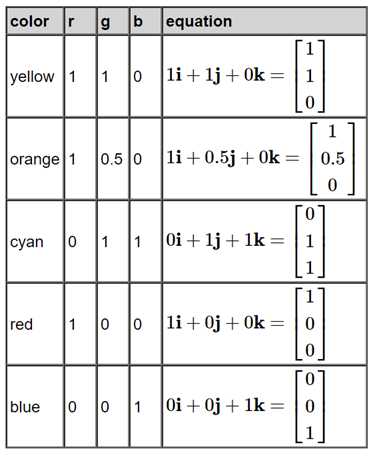
在上面的例子中,RGB原色i、j和k是根据它们自己的RGB颜色空间定义的,这使得这些值相当简单。当我们开始处理不同的颜色空间(如XYZ)时,事情变得更加有趣。
目标是找到与线性RGB空间的原色相匹配的三种XYZ颜色。一旦在XYZ空间中有了i、j和k,就可以使用相同的r、g和b标量来找到RGB颜色的XYZ值。我会马上讨论如何推导这些新的初值,但首先我们假设我们已经知道它们的值,这样我们就可以用一个例子来说明这个过程。设l是XYZ空间中的红色主元素,m是XYZ空间中的绿色主元素,n是XYZ空间中的蓝色边缘元素。
我们现在可以计算XYZ空间中的任何线性RGB颜色,将其作为XYZ空间中主色的线性组合。

如先前所示,从线性RGB空间到XYZ空间的转换矩阵具有从XYZ空间中的主要RGB颜色构建的列。为了找到这些值,我们需要将RGB空间的xy色度坐标用于红色,绿色,蓝色和白色。注意,我们只有x和y坐标。如前所述,我们可以根据x和y计算z坐标,但是我们需要X,Y或Z才能转换回XYZ坐标。就目前而言,我们没有足够的信息从xy色度空间到XYZ空间,但是按照我们转换的意图,我们可以再做一个假设。
让我们澄清一下此转换的目的。前面我提到过眼睛如何适应照明环境,以选择应被视为白色的颜色。为了我们的目的,我们希望将感知到的白色视为最大亮度。这意味着,如果我们从RGB空间A转换为XYZ空间然后再转换为RGB空间B,我们希望RGB空间A中的白色保持RGB空间B中的亮度。我们要做的就是确保当RGB空间转换为XYZ空间时,白色值始终以一致的Y(即一致的相对亮度)结束。
我提到过,只要我们保持一致,就可以为白点选择任何Y发光度,但是标准做法是使用Y值为1以获得全亮度。有时,您可能会看到100的Y表示全亮度,但是在这种情况下,标准值为1。有了白色的目标Y值,我们现在有足够的约束来求解矩阵。让我们列出我们开始的变量。
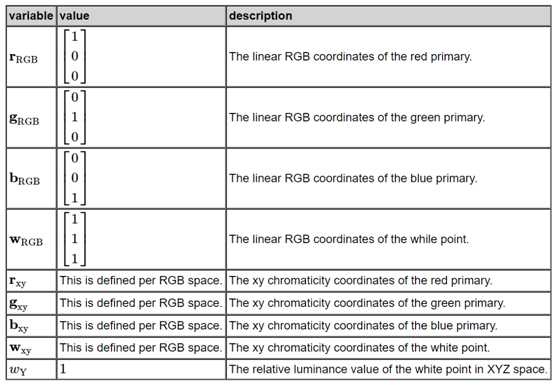
目标是求解列主变换矩阵M,它将从线性RGB空间转换到XYZ空间。第一步是使用前面讨论的方程z=1−x−y将所有xy色度坐标转换为xyz色度坐标。


我们知道所有的xyz初值,因此知道上面等式中的左矩阵。我们的未知数现在降到构成右矩阵的三个标量值。请注意,虽然每个标量都被写成X、Y和Z分量的和,但我们真正关心的只是求和结果,而不是各个部分。这就是为什么我说只有三个未知数,而不是九个。为了解决这三个未知数,我们将使用已知的白点RGB和XYZ值。因为M从RGB变换到XYZ空间,所以我们可以声明如下等式:
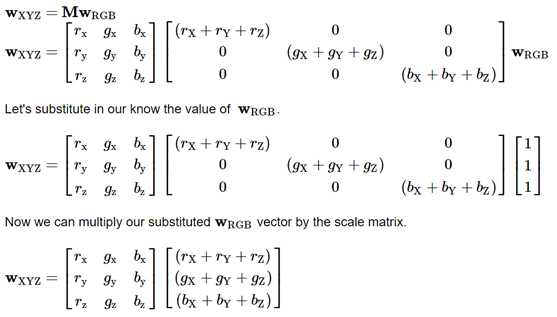
现在我们将把方程的每边乘以剩下的3x3矩阵的逆。这将把我们所有的已知值放在方程的左边,我们的未知值放在右边。如果您不熟悉3x3矩阵的逆运算,我将在本文的末尾提供代码,但出于理智起见,这里不会编写完整的推导。Google应该提供大量关于这个过程的结果,包括Wikipedia和Mathwords的这一个。
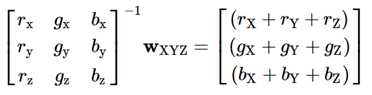
我们现在可以重建我们的RGB到XYZ转换矩阵M。将wXYZ向量乘以上述3x3矩阵的倒数将得到将主XYZ坐标转换为XYZ坐标的标量值。这是我们从M中分解出来的标量矩阵的三个未知数。
为了得到相反方向的矩阵变换(从XYZ空间到线性RGB空间),我们可以使用M的逆矩阵。我们也可以用与上面类似的方式来推导矩阵,但是在这么多类型化之后,仅仅使用逆似乎是一种更简单的方法。
标签:bsp 绿色 没有 变量 校正 加法 element 如何使用 nbsp
原文地址:https://www.cnblogs.com/wujianming-110117/p/13294643.html