标签:mamicode 5* eem inf ash title from 特征提取 sum
算法实现起来比较简单,参考 资料1,这里不再赘述;
傅里叶变换 的 基波 为 正弦波,如果原始信号波形很复杂,信号分解 计算量会很大,用 无穷多的 正弦波 才能 逼近 这个 波形;
小波变换 的 基波 为 某些固定波形,不同的 基波 对信号处理影响很大,一旦选定,无法更换,即使小波基在全局最佳,在某些局部却不一定;
经验模态分解的特点在于 自适应 的基函数(基波),使得它 可以处理 任意 信号;
经验模态分解 认为 任何 一个复杂信号 都可以分解成若干个 基本模态分量 imf;
这些基本模态分量相加 也可以 大致 重构 原始信号;
我们把 imf 进行 频谱分析后,频率最高的就是 噪声,把 这个 imf 以外的 imf 相加,就可以达到去燥效果;
import numpy as np import matplotlib.pylab as plt from PyEMD.EEMD import EEMD from scipy.fft import fft if __name__ == ‘__main__‘: t = np.linspace(0, 100, num=100) S = 3*np.sin(2*np.pi*10*t) # 10HZ S += 5*np.sin(2*np.pi*4*t) # 4HZ S += np.random.randn(100, ) # 白噪声 eemd = EEMD() imfs = eemd.eemd(S, T=t, max_imf=-1) print(imfs.shape) rows = 2 * imfs.shape[0] + 1 ### 信号重构 plt.subplot(311); plt.title(‘original‘) plt.plot(S) plt.subplot(312); plt.title(‘sum all imfs‘) sum_imf0 = np.sum(imfs, axis=0) plt.plot(sum_imf0) plt.subplot(313); plt.title(‘sum no noise imfs‘) sum_imf1 = np.sum(imfs[1:, :], axis=0) plt.plot(sum_imf1) plt.show()
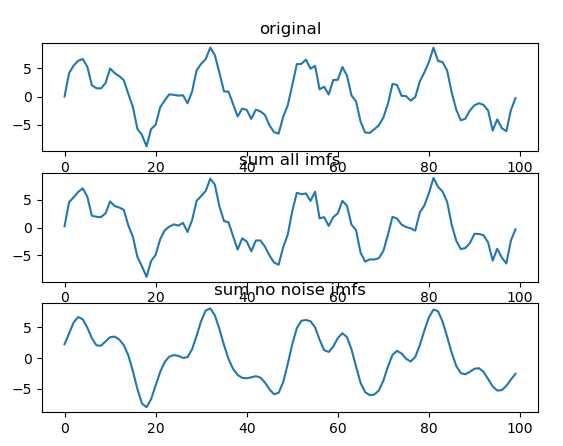
可以看到 第 2 个图 和 原始信号 基本一致;
第 3 个图 明显 光滑了,去燥的结果;
这些 imf 具有不同的特征尺度,比 原始信号更有规律性;
我们可以对 这些 imf 进行特征提取,如 幅值、频谱分析、样本熵计算 等;
接上面的代码,进行频谱分析;
plt.subplot(rows, 1, 1) plt.plot(S) for i in range(imfs.shape[0]): plt.subplot(rows, 1, i*2+2) plt.plot(imfs[i]) # imf 分量 y_fft = np.abs(fft(imfs[i])) # 傅里叶变换进行频谱分析 plt.subplot(rows, 1, i * 2 + 3) plt.plot(y_fft, ‘r‘) plt.show()
输出:第一个图是原始信号,后面 的 依次为 imf 分量 和 这个 imf 对应的 频谱
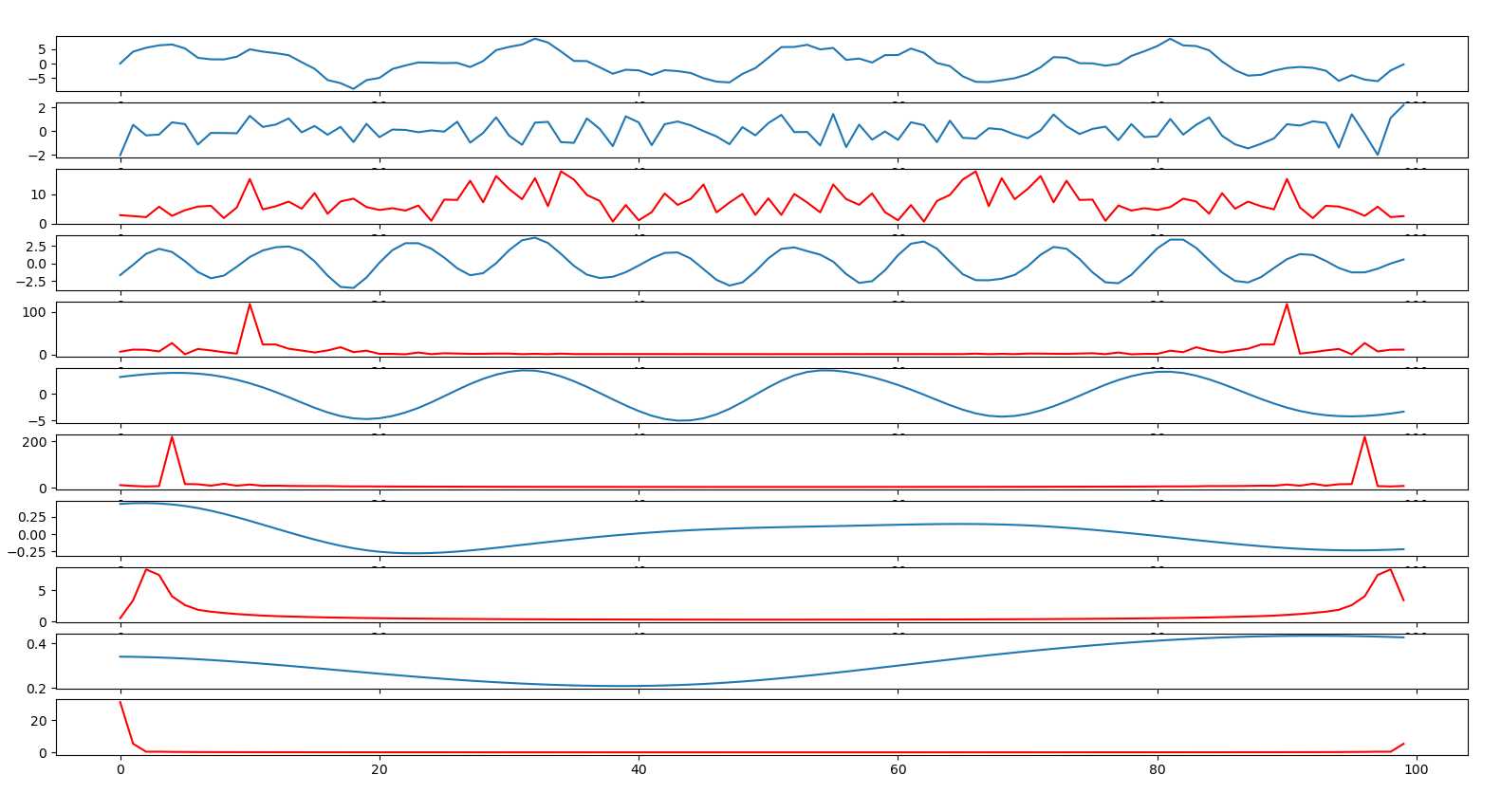
第一个 imf 分量 就是 白噪声,高频;
第二个 imf 分量 为 10HZ 的正弦波,频谱图 在 10HZ 处 凸起;
第三个 imf 分量 为 4HZ 的正弦波;
参考资料:
https://zhuanlan.zhihu.com/p/40005057 这篇文章能让你明白经验模态分解(EMD)——基础理论篇
标签:mamicode 5* eem inf ash title from 特征提取 sum
原文地址:https://www.cnblogs.com/yanshw/p/13294594.html