标签:正是 图片 table 产生 图形 margin 离散 分布 运算
《R语言的科学编程与仿真》的第18章提到,所有的随机变量可以通过处理U(0,1)随机变量生成。该书在18.2里给出了一个模拟算法,具体内容摘抄如下:
假设X是在集合{0,1,...}取值的离散随机变量,累积分布函数是F,概率质量函数是p。下面一段代码给定一个均匀随机变量U并返回一个累积分布函数是F的离散随机变量X。
# given U~U(0,1)
X<-0
while(F(X)<U){
X<-X+1
}
当这个算法结束时,我们有F(X)≥U和F(X-1)<U,因此
P{X=x}=P{F(x-1)<U≤F(x)}=F(x)-F(x-1)=p(x)
正是所需要的。
基于上述想法,这里用均匀分布来生成泊松分布,并画图比较。首先是写一个函数来产生由均匀分布生成的服从泊松分布的随机变量的取值,其次是进行重复试验,运用频率来估计随机变量取该值的概率,最后是画图进行比较。
#第一步,生成模拟函数
poiss_sim<-function(lambda){
x<-0 # 初始值定为0
px<-exp(-lambda)
Fx<-px
U<-runif(1)
while(Fx<U){
x<-x+1
px<-px*lambda/x # 利用泊松分布的概率密度函数p(x)和p(x-1)存在的递归关系,简化运算
Fx<-Fx+px # Fx即为分布函数F(x)
}
return(x)
}
#第二步,重复试验,这里的实验次数N定为10000次
N<-1e4
lambda<-2
x<-replicate(N,poiss_sim(lambda=lambda))
y<-table(x)
names<-as.numeric(names(y))
freq<-as.numeric(y)
phat<-vector(length=length(names))
for(i in names){
phat[i+1]<-sum(x==i)/N
} # 用频率估计概率
#第三步,和R自带的函数dpois()进行图形比较
par(las=1)
plot(names,dpois(names,lambda=lambda),xlab=‘x‘,ylab=‘p(x)‘,type=‘h‘)
points(names,dpois(names,lambda=lambda),pch=19)
points(names,phat,pch=3)
legend(6,0.25,legend=c(‘reality‘,‘simulation‘),pch=c(19,3),bty=‘n‘,cex=2)
图形如下:
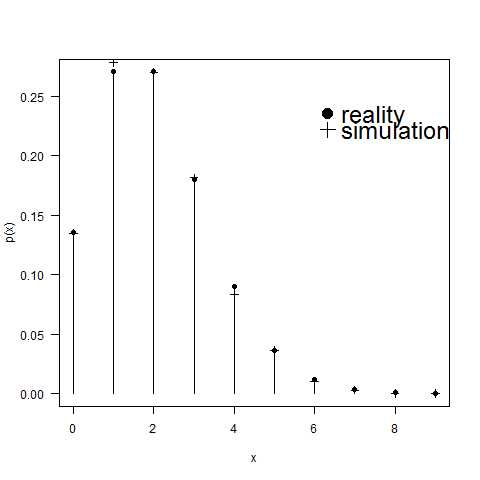
可以看出,真实值和模拟值还是很接近的!
标签:正是 图片 table 产生 图形 margin 离散 分布 运算
原文地址:https://www.cnblogs.com/Enjoy-Respect-9527/p/13298389.html