| Time Limit: 1000MS | Memory Limit: 30000K | |
| Total Submissions: 820 | Accepted: 255 |
Description
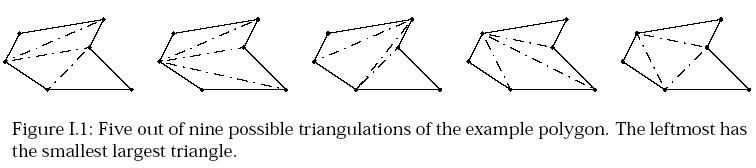
Input
Output
Sample Input
1 6 7 0 6 2 9 5 3 5 0 3 1 1
Sample Output
9.0
Source
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#define maxn 10e9
#define eps 1e-8
using namespace std;
double s[55][55][55];
double d[55][55];
int n,m;
struct Point
{
double x,y;
} p[55];
double cross(Point a, Point b, Point c)
{
return (b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y);
}
double area(Point a, Point b, Point c)
{
return fabs(cross(a, b, c)/2.0);
}
bool judge(int i, int k, int j)
{
for(int t=0; t<m; t++)
{
if(t==i||t==k||t==j) continue;
double tmp=area(p[i],p[k],p[j])-area(p[i],p[j],p[m])-area(p[i],p[k],p[m])-area(p[j],p[k],p[m]);
if(fabs(tmp-s[i][k][j])<eps)
return false;
}
return true;
}
int main()
{
// freopen("input.txt","r",stdin);
//freopen("output.txt","w",stdout);
cin>>n;
while(n--)
{
memset(d,0,sizeof(d));
cin>>m;
for(int i=0; i<m; i++)
cin>>p[i].x>>p[i].y;
for(int i=0; i<m; i++)
for(int j=0; j<m; j++)
for(int k=0; k<m; k++)
s[i][k][j]=area(p[i],p[k],p[j]);
for(int l=2; l<=m-1; l++)
for(int i=0; i+l<=m-1; i++)
{
int j=i+l;
d[i][j]=maxn;
for(int k=i+1; k<j; k++)
if(judge(i,k,j))
d[i][j]=min(d[i][j],max(s[i][k][j],max(d[i][k],d[k][j])));
}
printf("%.1lf\n",d[0][m-1]);
}
return 0;
}
原文地址:http://blog.csdn.net/dojintian/article/details/40988289