f2m

As a very small example, consider the field F₂4, defined by using polynomial representation with the irreducible polynomial f(x) = x⁴ + x + 1. 

The element g = (0010) is a generator for the field . The powers of g are: 

g⁰ = (0001) g¹ = (0010) g² = (0100) g³ = (1000) g⁴ = (0011) g⁵ = (0110) 

g⁶ = (1100) g⁷ = (1011) g⁸ = (0101) g⁹ = (1010) g¹⁰ = (0111) g¹¹ = (1110) 

g¹² = (1111) g¹³ = (1101) g¹⁴ = (1001) g¹⁵ = (0001) 

In a true cryptographic application, the parameter m must be large enough to preclude the efficient generation of such a table otherwise the cryptosystem can be broken. In today‘s practice, m = 160 is a suitable choice. The table allows the use of generator notation (g^e) rather than bit string notation, as used in the following example. Also, using generator notation allows multiplication without reference to the irreducible polynomial 

f(x) = x⁴ + x + 1. 

Consider the elliptic curve y² + xy = x³ + g⁴x² + 1. Here a = g⁴ and b = g⁰ =1. The point (g⁵, g³) satisfies this equation over F₂m : 

y² + xy = x³ + g⁴x² + 1 

(g³)² + g⁵g³ = (g⁵)³ + g⁴g¹⁰ + 1 

g⁶ + g⁸ = g¹⁵ + g¹⁴ + 1 

(1100) + (0101) = (0001) + (1001) + (0001) 

(1001) = (1001) 

The fifteen points which satisfy this equation are: 

(1, g¹³) (g³, g¹³) (g⁵, g¹¹) (g⁶, g¹⁴) (g⁹, g¹³) (g¹⁰, g⁸) (g¹², g¹²) 

(1, g⁶) (g³, g⁸) (g⁵, g³) (g⁶, g⁸) (g⁹, g¹⁰) (g¹⁰, g) (g¹², 0) (0, 1) 

These points are graphed below: 

Next

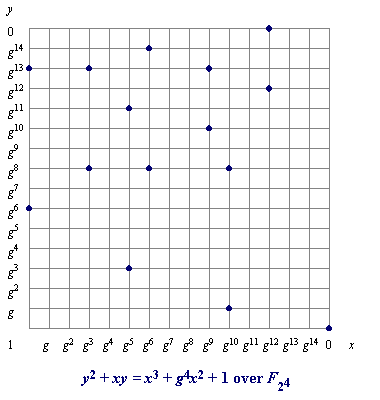
There are finitely many points on a curve over F₂m .

Elements of the field F₂m are m-bit strings. The rules for arithmetic in F₂m can be defined by either polynomial representation or by optimal normal basis representation. Since F₂m operates on bit strings, computers can perform arithmetic in this field very efficiently. 

An elliptic curve with the underlying field F₂m is formed by choosing the elements a and b within F₂m (the only condition is that b is not 0). As a result of the field F₂m having a characteristic 2, the elliptic curve equation is slightly adjusted for binary representation: 

y² + xy = x³ + ax² + b 

The elliptic curve includes all points (x,y) which satisfy the elliptic curve equation over F₂m (where x and y are elements of F₂m ). An elliptic curve group over F₂m consists of the points on the corresponding elliptic curve, together with a point at infinity, O. There are finitely many points on such an elliptic curve.