数据结构-树-二叉树遍历的实例-02

标签：and   先序   递归   getheight   不同   focus   link   lib   image   

输出二叉树中的叶子结点

void PreOrderPrintLeaves( BinTree BT ) {     
    if( BT ) {         
        if ( !BT-Left && !BT->Right )// 在二叉树的遍历算法中增加检测结点的“左右子树是否都为空”。            
            printf(“%d”, BT->Data );     
        PreOrderPrintLeaves ( BT->Left );             
        PreOrderPrintLeaves ( BT->Right );     
    } 
}

再先序遍历中，如果一个结点的左右子树都是空，那么输出

求二叉树的深度

int PostOrderGetHeight( BinTree BT ) 
{       int HL, HR, MaxH;     
        if( BT ) { 
　　　　　 HL = PostOrderGetHeight(BT->Left);  /*求左子树的深度*/          
　　　　 　HR = PostOrderGetHeight(BT->Right); /*求右子树的深度*/          
　　　　　 MaxH = （HL > HR）? HL : HR; /*取左右子树较大的深度*/             
　　　　　 return ( MaxH + 1 ); /*返回树的深度*/    
        }     
        else  return 0; /* 空树深度为0*/ 
} 

如何去深入理解呢？

1、首先我们知道递归要找到函数的结束条件，而这个函数结束的条件就是BT->NULL的时候，由于空树的深度为0，那么最后每个叶节点的HR和HL都是0。

2、其次，？号运算符代表成立取前面的值，不成立取后面的值，由于都是0，该条件不成立，那么MaxH取后面的值HR，所以这个函数返回值MaxH +1 = 1。

3、所有叶结点的返回值是1，那么叶节点上一级结点调用它的时候就会得到HR（叶结点的返回值MaxH +1） = 1，HL = 1，所以上一级结点的返回值是2……以此类推，最后会返回最大的深度。

https://www.bilibili.com/video/BV1g741137Wq?from=search&seid=13740021077770885547

二元运算表达式树及其遍历

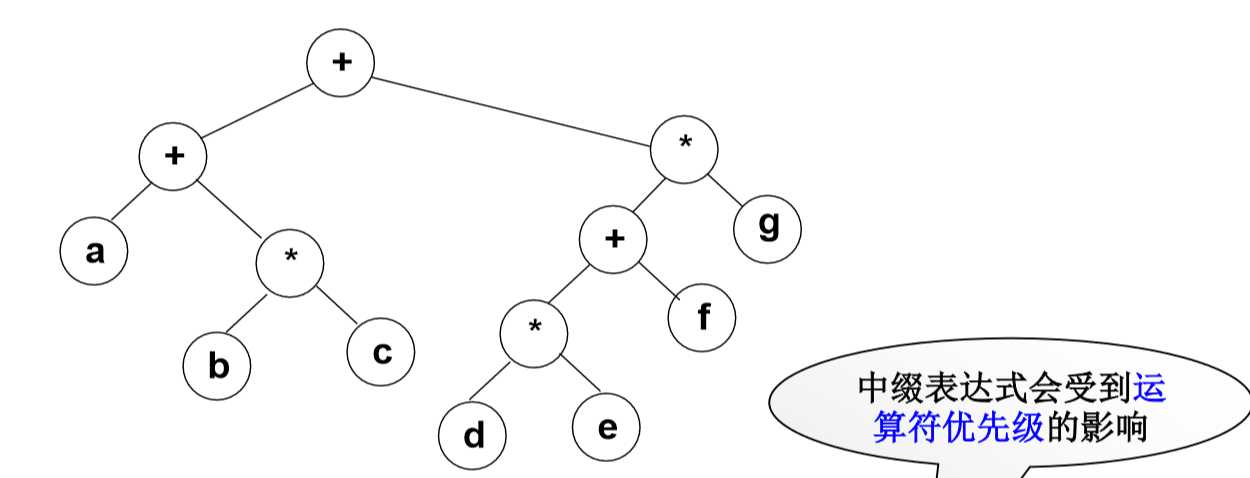
算子保存在叶结点中，运算符保存在根节点中，利用遍历可以得到三种不同的访问结果：

• 先序遍历得到前缀表达式：+ + a * b c * + * d e f g

• 中序遍历得到中缀表达式：a + b * c + d * e + f * g

• 后序遍历得到后缀表达式：a b c * + d e * f + g * +

由两种遍历序列确定二叉树

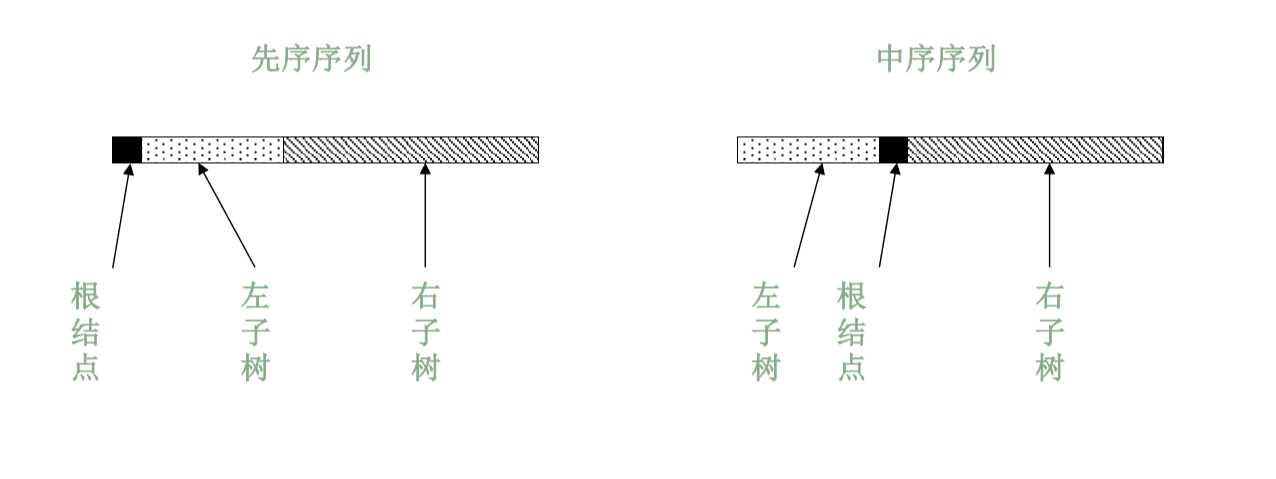
必须要有中序遍历才可以通过两种遍历确定二叉树的排布，否则无法知道谁在中间，例子如下（先序和中序遍历序列来确定一棵二叉树 ）：

• 根据先序遍历序列第一个结点确定根结点

• 根据根结点在中序遍历序列中分割出左右两个子序列

• 对左子树和右子树分别递归使用相同的方法继续分解。

数据结构-树-二叉树遍历的实例-02

标签：and   先序   递归   getheight   不同   focus   link   lib   image   

原文地址：https://www.cnblogs.com/lingxueqian/p/13305162.html