正则表达式几乎每个程序员都会用到，对于这么常见的一个语言，有没有想过怎么去实现一个呢？乍想一下，也许觉得困难，实际上实现一个正则表达式的引擎并没有想像中的复杂，《编译原理》一书中有一章专门讲解了怎么基于状态机来构建基本的正则表达式引擎，讲这个初衷是为词法分析服务，不过书里的东西相对偏理论了些，实现起来还是要费些功夫的，只是它到底指明了一条路，当然，书里只针对基本的语法进行了分析讲解，对于在实际中有些非常有用的很多扩展语法，它就基本没有涉及了，这些扩展的语法中有些是比较好实现的，有些则很难。
正则表达式由字符与元字符组成，整个表达式用于描述符合某些特征的字符串，比如说：abc，表示“abc"这个字符串，由‘a‘,‘b‘,‘c‘三个字符按顺序连接在一起。 基本的正则表达比较简单，主要包括以下操作符及元字符(meta-character)：
上述描述的操作符有优先级的区别，最弱的是或操作符，其次是连接，最后是重复操作符，比如abc|efg，就等价于(abc)|(efg)。
由前面的说明，我们可以发现基本的正则表达式相对来说是比较弱的，语法上也很简单，容易实现的同时不可避免地相对功能就偏弱，于是就有了扩展的语法，扩展的语法相对就复杂了，我就不一一介绍，具体可以参考维基百科上的描述，对于本文来说，主要想实现其中的如下几个语法：
加入这几个语法，主要是因为它们太常用也太有用了，前面两个也还好实现，向后引用这个却是很麻烦的，而且实现起来效率很低，后面会介绍。
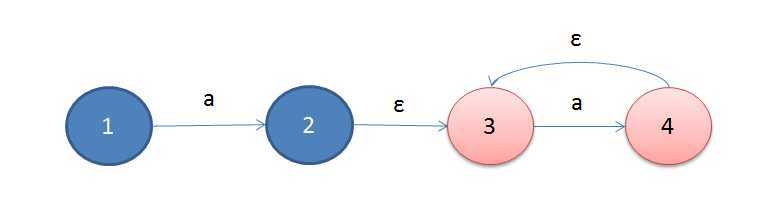
实现正则表达式引擎，目前来说流行的做法主要有两种，一种是各大语言里(perl, python,etc）常用的回溯法(backtracking)，一种是龙书里说的基于状态机的做法。二者的实现各有优劣，回溯法相对来说实现功能较容易，但算法效率很低，状态机的实现，最大的优点是效率很高，但对于扩展的语法实现起来比较困难，而且代码相对不好理解。 对于基本的正则表达式语法来说，用状态机实现是很理想的，性能很高，而且比较容易实现，龙书里所说的ε-NFA(non-deterministic finite automata)是这样一种状态机，首先就是某些状态对同一个输入，它可以有多个不同的转换，然后就是除了一般状态机所具有的状态与具体转换之外，还加入了一种叫作ε的状态及ε转变：
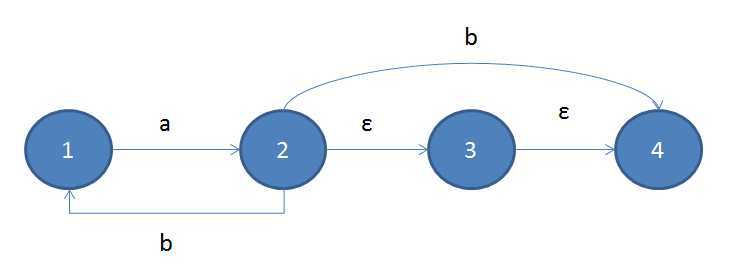
如上图所示，状态3就是我们所说的ε状态，该状态只能通过ε转换从别的状态转过来，也只能通过ε转换变转到其它状态，其中，ε转换指的是不需要任务输入就可以进行的转换。ε状态与ε转换的加入让状态机的构建更加容易与清晰，同时在某些情况下也使得一些特殊功能更加好实现，但是ε状态过多也是有坏处的，它使得状态机的状态转变复杂变冗余了，因此应该尽可能的少用。
一条完整的正则表达式可以看成是一系列小的正则表达式的组合，这些组合的关系根据前面的介绍主要可以概括为如下几种：
将正则表达式转换为ε-NFA的原则就是先从小的正则表达式开始，先将单个字符转为各个小的ε-NFA，再将这些ε-NFA根据组合关系拼凑成完整的ε-NFA。
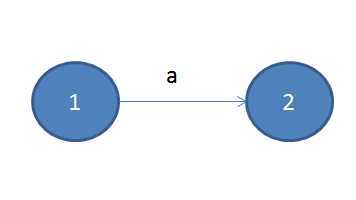
对于单个字符来说，它的ε-NFA很简单，只有两个状态，一个转换：
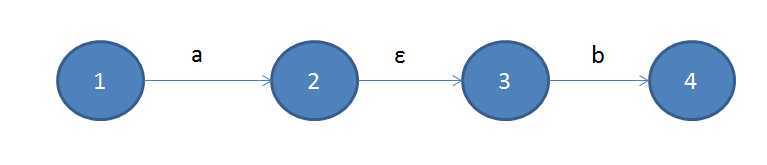
concat组合则主要是将两个ε-NFA用ε转换连起来：
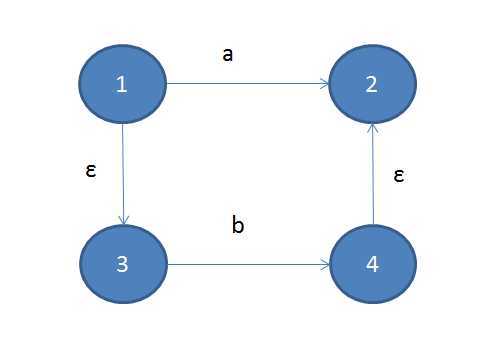
接下来是或组合：
对于重复组合来说，情况稍微复杂，其中‘?‘, ‘+‘, ‘*‘，我们只需要在子ε-NFA的开始与结束状态之间加入ε转换则可，如下所示：
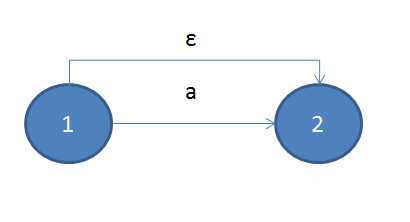重复一次或0次
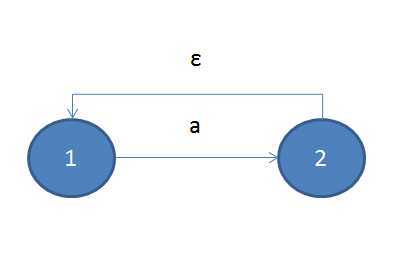重复至少一次
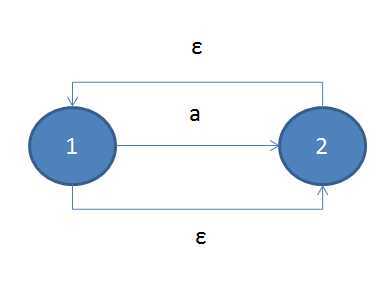重复任意次
对于扩展语法中的指定重复次数，我们可以采取将状态直接复制的做法，比较暴力，但管用，如：(a){2, 4}，我们得到如下ε-NFA
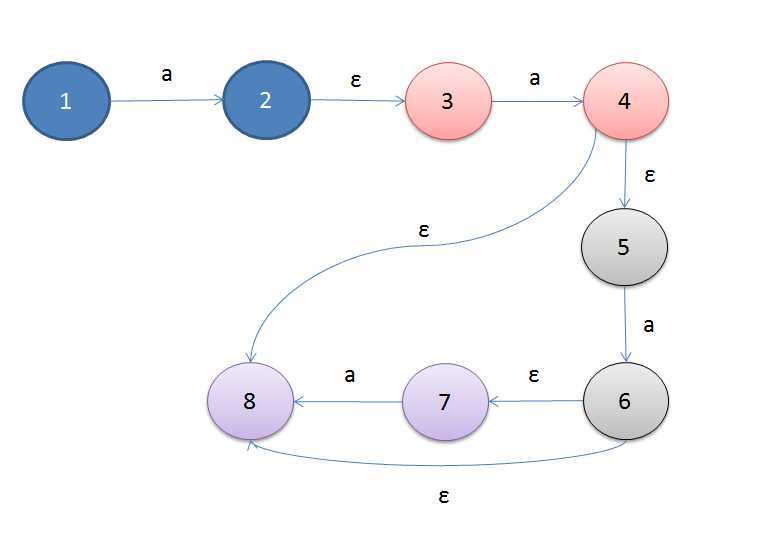
注意其中后三组不同颜色的状态，它们是从第一组状态复制过来的。 扩展的语法里，还包括如:{0,≌}这样的重复，我们只要把状态按最小的重复次数复制一遍，然后像+，*样加ε转换就行了：如{2,≌}
前面描述了怎么将小的ε-NFA组合成大的ε-NFA，我们知道，关键是先从小的正则表达式开始，但是具体在面对正则表达式时，我们怎么把一条完整的正则表达拆成小的正则表达式呢？
为了将大正则拆成小的正则，我们可以借助语法树的帮助，所谓的语法树在这里是指这样的一棵树，它的内部结点是操作符，内部节点的子树则是该操作符的操作数，而叶结点则是具体的符号，在这里操作符只有三种：或(or),
concat, 重复(统一用star表示), ，如：我们可以将(ab)+cd(e|f)转换为如下一棵语法树：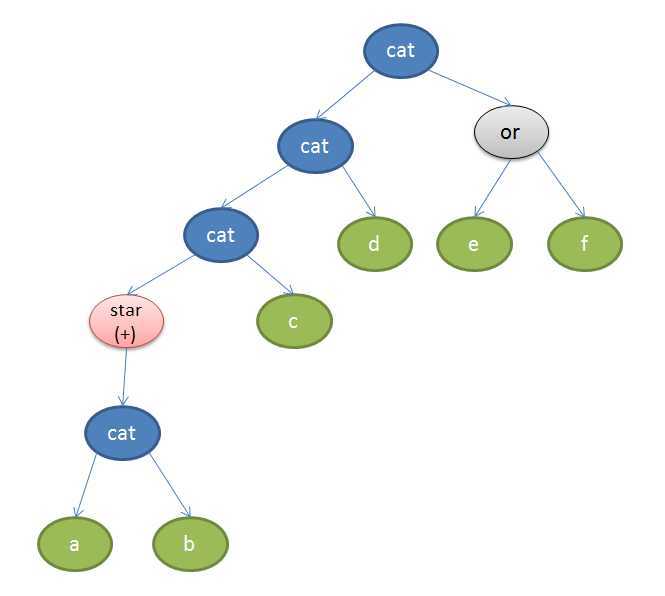
显然对于任意一个内部结点来说，它的左右子树，就分别代表了一个小的正则表达式，而叶子结点则是最小的，解释这样一棵树显然简单多了，至于怎样构建语法树，仔细想想，在正则表达式里，表达式与操作符是右结合的，如：a+, 然后两个表达式之间要么是是concat组合，要么是或组合，所以我们在构造语法树时，可以考虑从右往左，依次将各个小的表达式抽出来，然后对该小的正则表达式构建语法树则可。
```cpp
TreeNode* ConstructSynTree(const char* regstart, const char* regend)
{
const char* right_exp = ExtractExpression(reg_start, reg_end);
int operator = GetOperator(right_exp - 1);
TreeNode* node = CreateInteriorNode(operator);
TreeNode* left_child = ConstructSynTree(reg_start, right_exp - 2);
TreeNode* right_child = ConstructSynTree(right_exp, reg_end);
node->left = left_child;
node->right = right_child;
return node;
}
```
详细代码可以参考这里。
前面讲的内容主要是针对基本的正则表达式语法，原理主要来自龙书的介绍，只是在实现上我尽可能减少了ε状态，因为没有涉及扩展语法，前面的算法写起来是很简单的，大概只需要一千行左右代码就可以写出来，而且效率是很高的，只是因为太简单使用起来不方便，只能玩玩，下面我讲一下怎么实现前面提到几个扩展语法。
首先是关于重复，这个比较简单，前面已经讲了，至于匹配头(^),匹配尾($)，这个实现也比较容易，只要分加一个ε状态，对于匹配头时，该状态只有一个向外的ε转换，对于匹配尾时，该ε状态对任何输入都转换为自己则可：
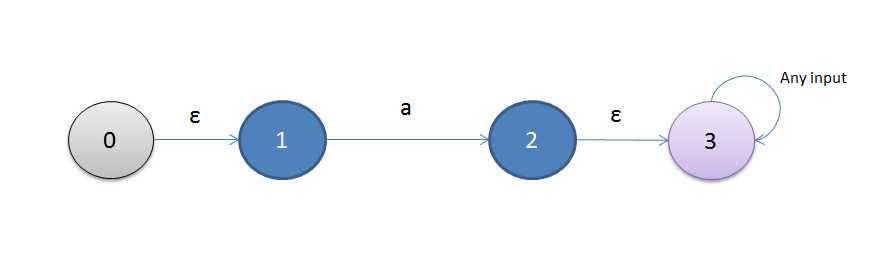
而至于向后引用，这个语法在现实中是很实用的，因此我才想着要把它加进来，但等到真正实现时，才发现这个功能却出乎意料的难以实现，根据这篇文档的介绍，正则表达式中向后引用的实现是一个NP完全问题，到目前来说，还没有发现高效的实现方法，而我面对的问题已经不是高效不高效的问题，而是在一个简单的ε-NFA状态机框架上要加入这个功能都是比较痛苦的，至于我现在的实现，已经把原先的状态机给hack了才做出来，代码也写得很难看了，这个以后得再想想能不能把实现设计的好一点。
要想实现这个向后引用，关键在于及时把前面括号里的正则表达式所捕获的内容保存下来，而一般来说，状态机的状态本身应该是没有状态的，它不应该记住它在前一个状态做了什么事情，这些限制都让实现很为难。 但是为了捕获括号里的正则表达式所匹配的内容，我们又必须清楚地知道，当前状态机是否进入了某个括号的正则表达式里，以及什么时候退出了该括号，为达到这个效果，我们在构建状态机时，可以引入两个特殊的ε状态，其中一个状态称作ε-unit-start，用来表示，下次输入如果导致当前状态发生转换，则需要开始保存后续的输入，另一个状态称作ε-unit-end，用来表示，如果进入了该状态，则如果后续输入导致该状态被转换出去，则应该停止保存后续的输入。
想法是这样，但实现起来有很多细节需要注意，因为是ε-NFA，对于每一个输入，状态机可能会得到好多个新的状态，因此：
这些都需要一一处理好，特别是类似(a),(a), a(cd)*fe这种表达式，括号里可能捕获空内容的情形。
我实现基本的正则表达式，只花了二三天时间，但为了使现这个向后引用，却反复修改，二三个星期才搞好。。。
现在代码差不多写好了，有兴趣的可以去瞄瞄，先从unit test看起，代码确实可读性有些差，做好心理准备就是了。
基于ε-NFA的正则表达式引擎,布布扣,bubuko.com
原文地址：http://www.cnblogs.com/catch/p/3722082.html
