标签：int   targe   debug   print   tco   位置   数列   图片   class   

斐波那契数列和零钱兑换

说到递归，就不得不提大名鼎鼎的斐波那契数列，这个最早接触应该还是高中数学的数列部分，后来学C语言的时候，老师讲递归就是举的这个例子。表达式如下：

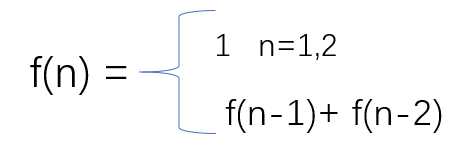
代码就是下面这个样子：

    public static int fib(int num) {
        if (num == 1 || num == 2) {
            return 1;
        }
        int a = fib(num - 1);
        int b = fib(num - 2);
//        return fib(num-1)+fib(num-2); 写在一行 调试看不清
        return a + b;
    }
    public static void main(String[] args) {
        int fib = fib(6);
        System.out.println(fib);
    }

执行过程就是这个样子：

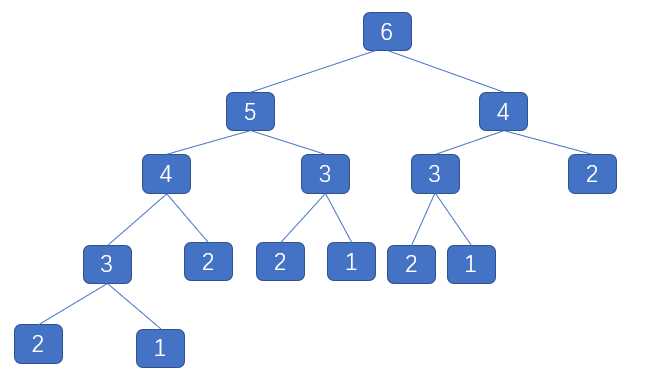
一直很困惑，到底是怎么执行的，直到遇到idea这个强大的工具，才算是比较清楚了。

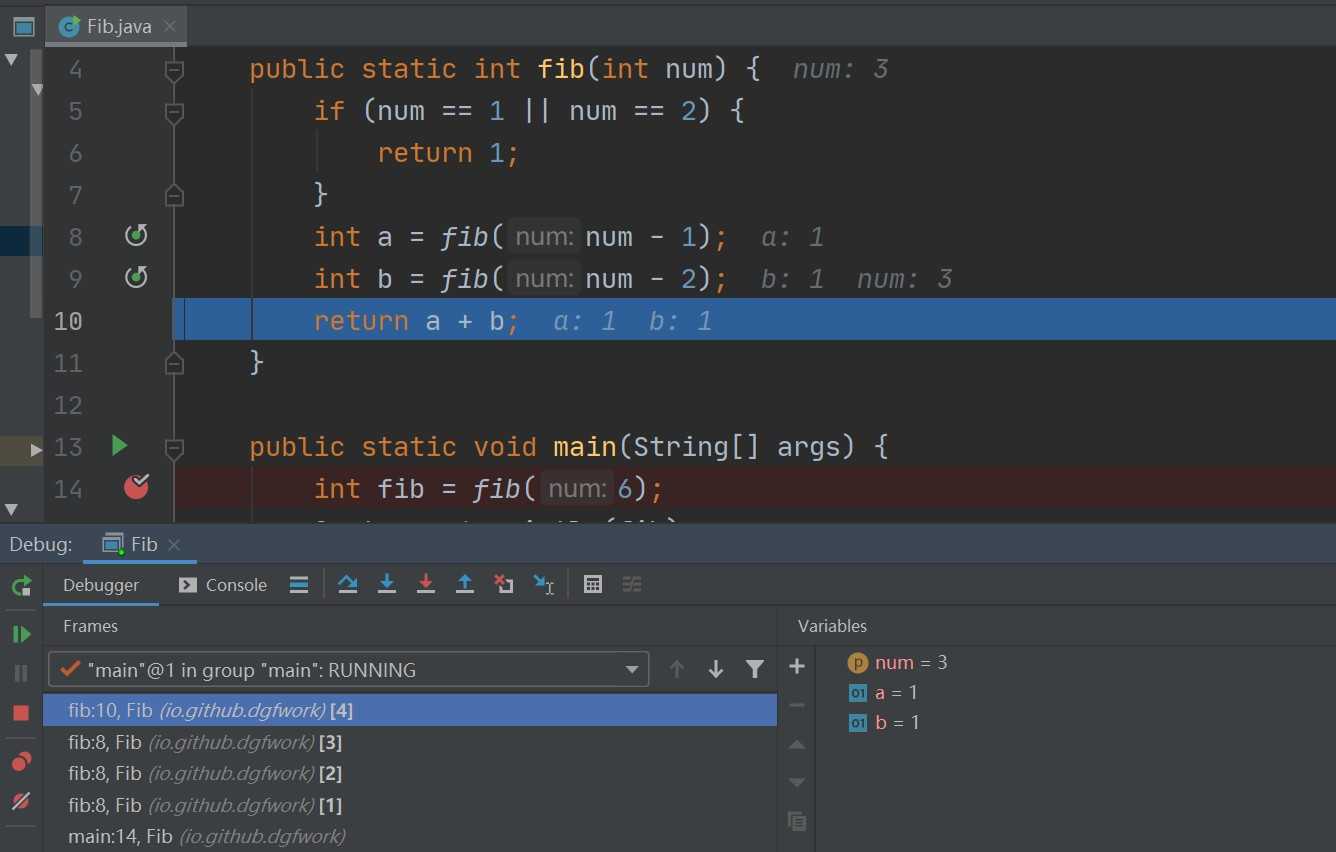
配合上面那个二叉树和这个debug的图，可以清楚的看到执行到什么位置了，每一次递归进去都会开一个新的Frames，见上图左下角。跟一遍就会发现，这个确实进行了很多重复计算。

于是动态规划出现了~

    public static int fib1(int num) {
        if (num == 1 || num == 2) {
            return 1;
        }
        int[] dp = new int[num + 1];
        // 初始化
        dp[1] = dp[2] = 1;
        // 将计算过的记下来，这样就大大减少了重复计算的内容
        for (int i = 3; i <= num; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[num];
    }

这样效率就大大提高了。

另一个类似的问题是零钱兑换，这个和斐波那契数列基本一样的。

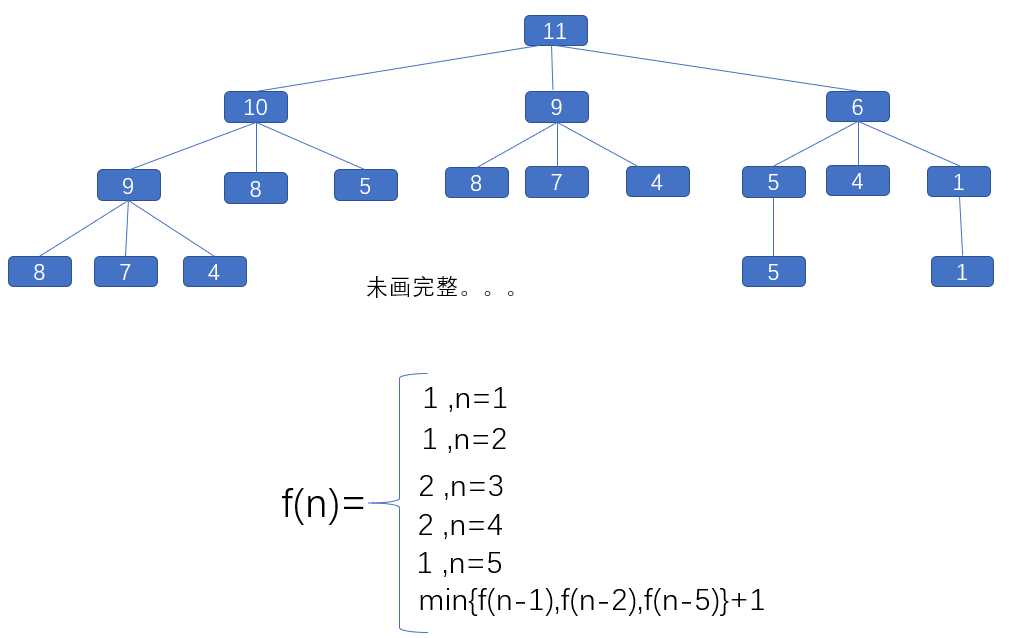
递归：

public class CoinChange {
    public static int coinChange(int target) {
        if (target == 1 || target == 2 || target == 5)
            return 1;
        if (target == 3 || target == 4)
            return 2;
        int a = coinChange(target - 1);
        int b = coinChange(target - 2);
        int c = coinChange(target - 5);
        return Math.min(a, Math.min(b, c)) + 1;
    }
    public static void main(String[] args) {
        int res = coinChange(40);
        System.out.println(res);
    }
}

    public static int coinChange1(int target) {
        int[] dp;
        if (target <= 5) {
            dp = new int[6];
        } else {
            dp = new int[target + 1];
        }
        // 初始化 
        dp[0] = 0;
        dp[1] = dp[2] = dp[5] = 1;
        dp[3] = dp[4] = 2;
        for (int i = 6; i <= target; i++) {
            dp[i] = Math.min(dp[i - 1], Math.min(dp[i - 2], dp[i - 5])) + 1;
        }
        return dp[target];
    }

斐波那契数列和零钱兑换

标签：int   targe   debug   print   tco   位置   数列   图片   class   

原文地址：https://www.cnblogs.com/d9e84208/p/13307660.html