标签:ret tps scanf -- 信息 初始 大小 代码 alc
感谢\(ivorysi\)学姐_(:з」∠)_给我讲了一上午才明白
后缀自动机 \({\rm (Suffix\ Automaton,SAM)}\)是一个用来匹配单模板串的所有子串的算法。
\({\rm SAM}\)的空间复杂度、构造的时间复杂度都是\(O(n)\)的。
后缀自动机是一个\({\rm DAG}\)。
顾名思义,后缀自动机上,根到每个节点的路径都代表一个原串的后缀。
对于字符串\(\texttt{aabb}\),它的后缀自动机为:
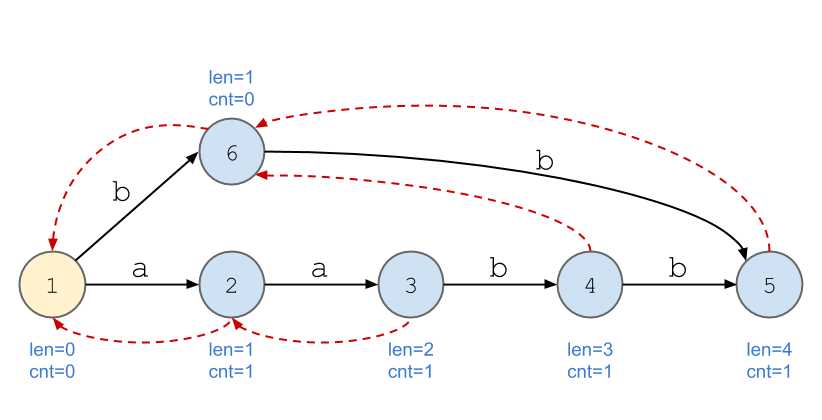
设根节点为\(1\),加入到第\(R\)位,存在\((1,i]\)是\((1,R]\)的后缀且长度最大,即\((1,i] = (L,R]\)且\(i\)最大,则\(fa[R]=i\)。
\(|L,R|\)可以为\(0\),即\(fa[R] = 1\)。
有点类似于AC自动机的失配函数。
每个节点需要储存的信息有:
\(ch[26]\):子节点
\(fa\):父节点
\(len\):从根节点到该节点的(代表的字符串的)长度
\(cnt\):\(0/1\),若该节点在后缀链上,则为\(1\)
需要储存的信息有:
\(root\):根节点
\(last\):上一个加入的节点(每次\(+1\))
\(siz\):后缀自动机的节点个数
设当前插入的字符为\(x\).
依旧以串\(\texttt{aabb}\)为例。

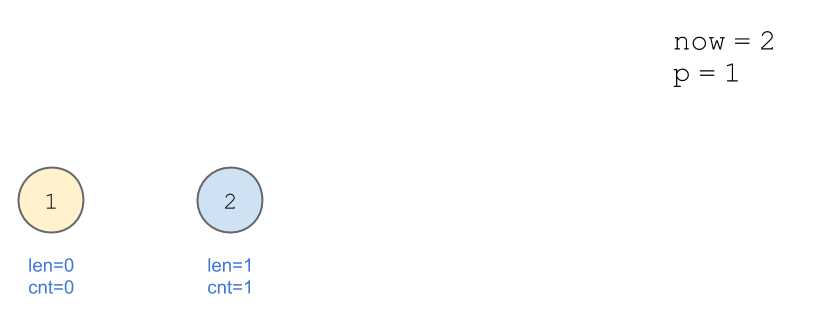
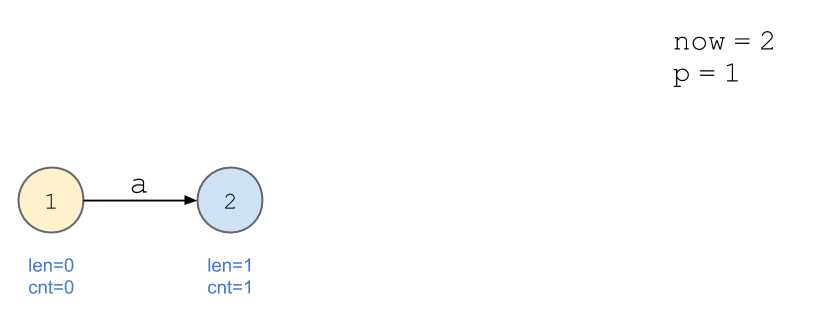
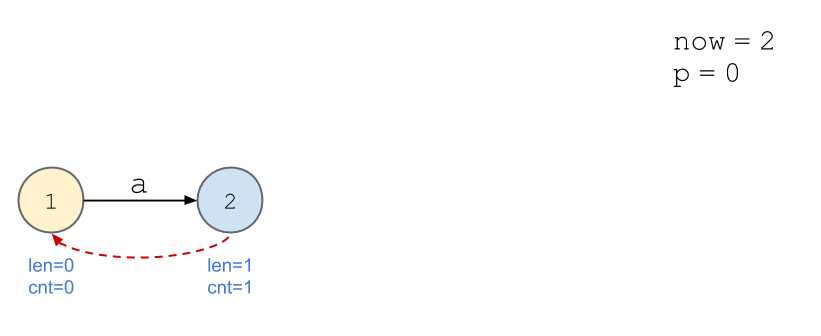
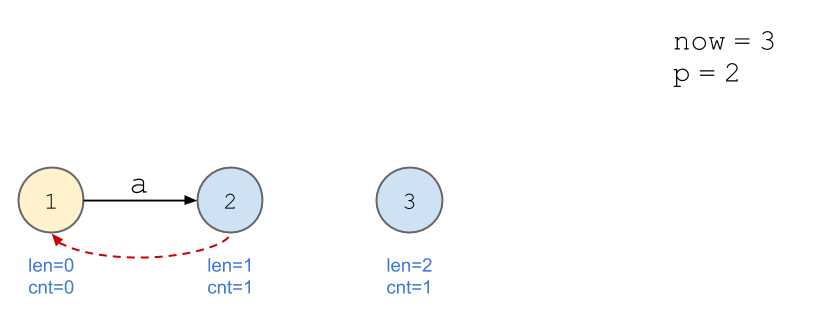
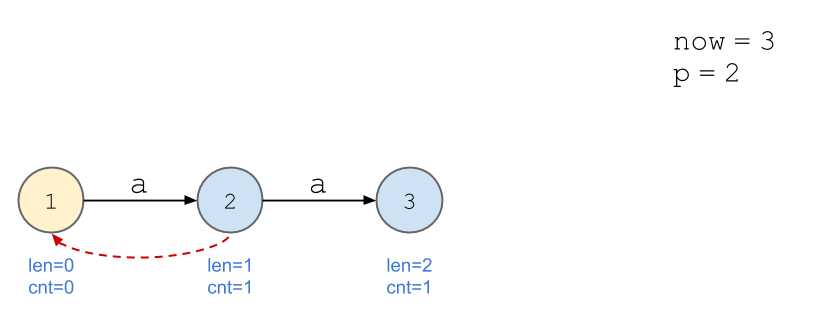
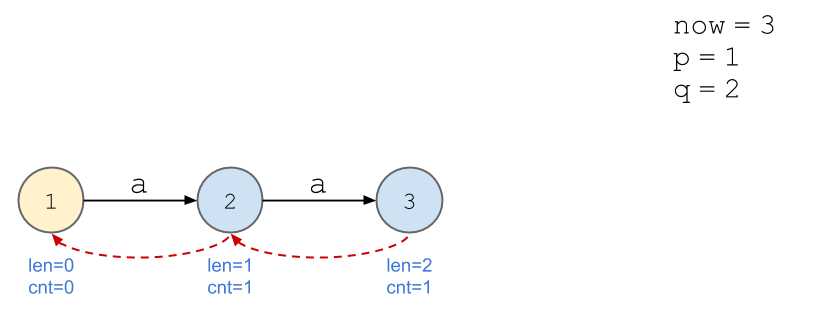
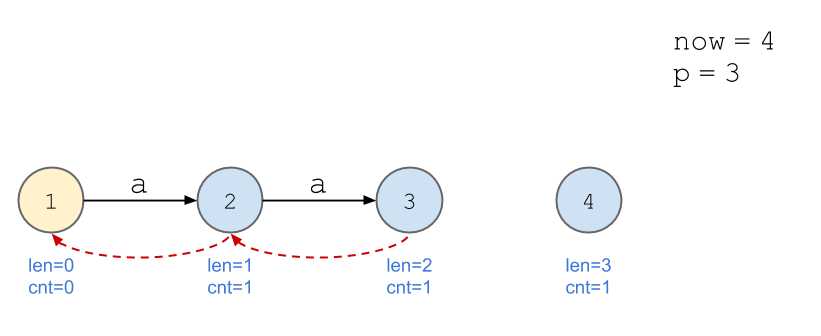
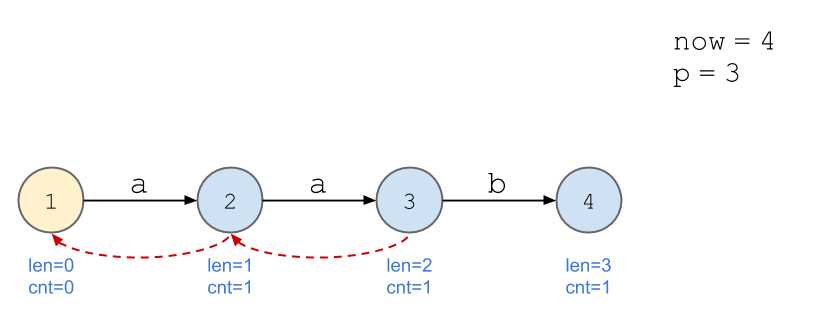
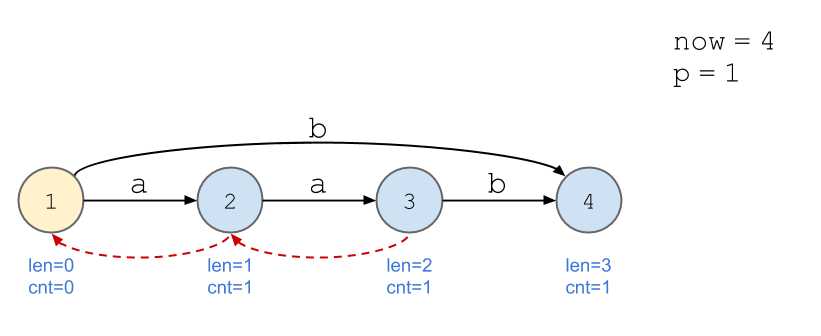
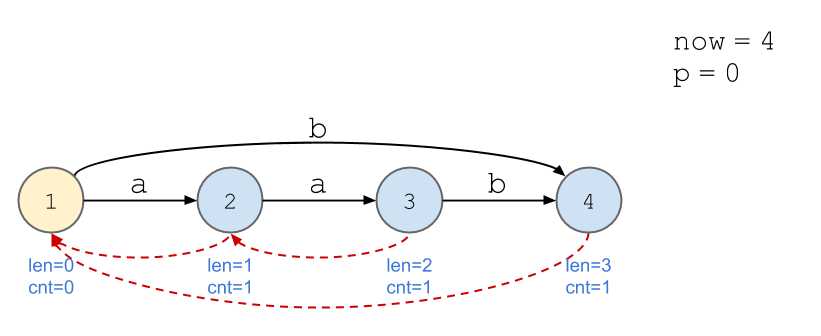
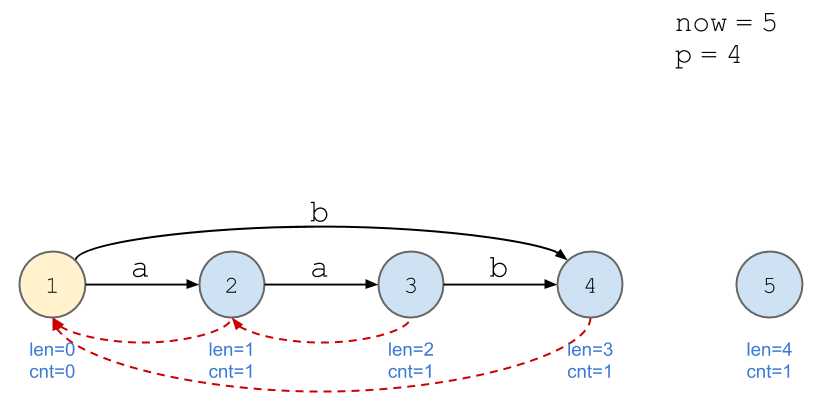
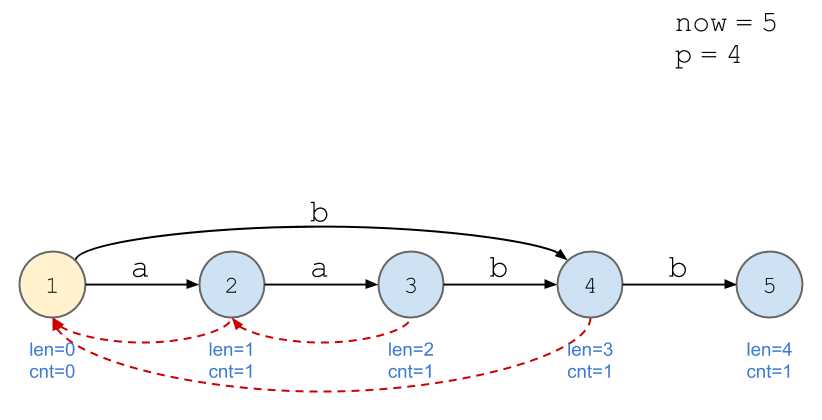
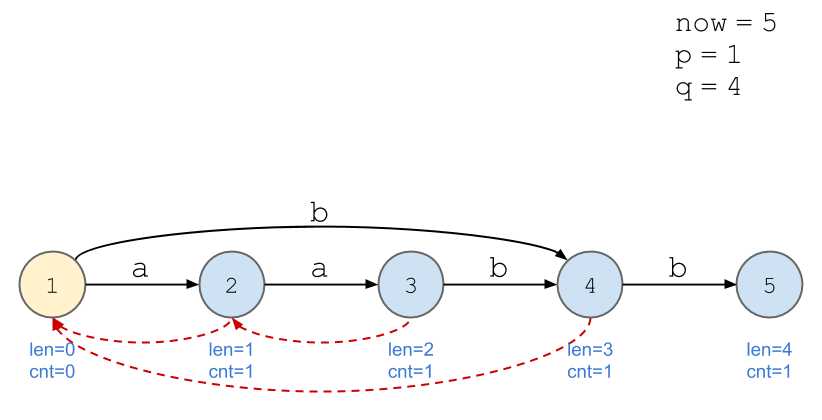
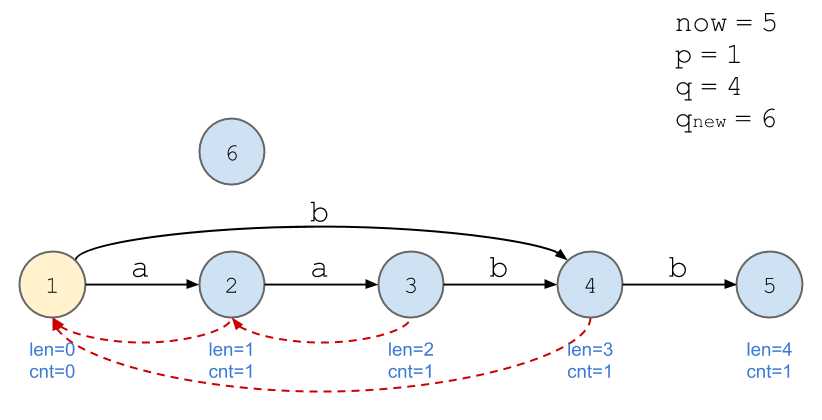
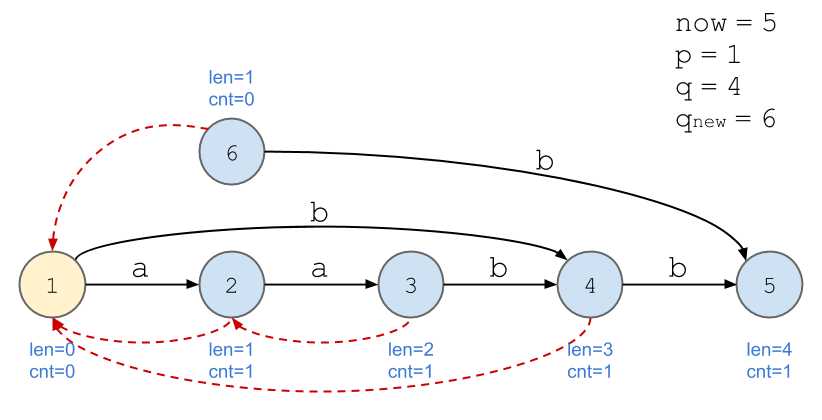
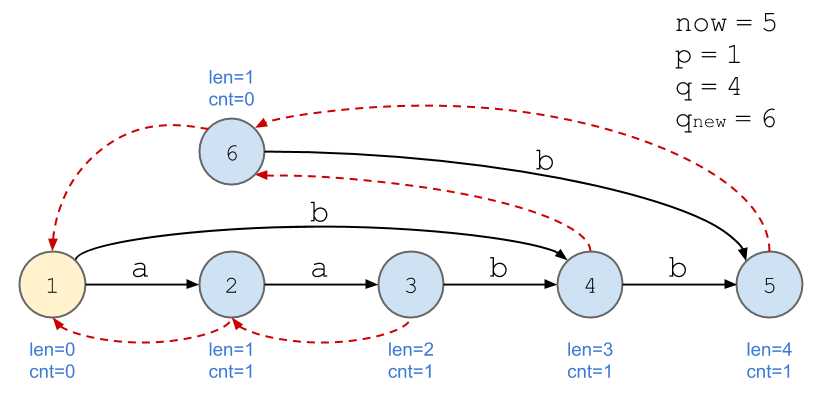
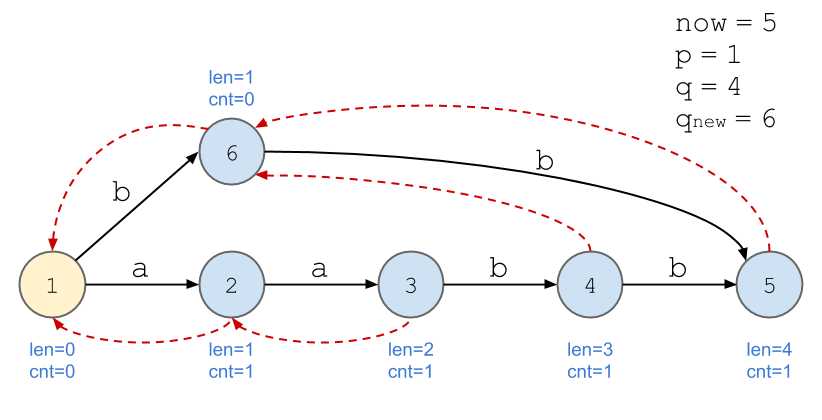
画图好累...
我的理解:以上述例子为例,当加入第四位,即第二个\(\texttt{b}\)时,后缀\(\texttt{b}\)的出现次数不再与\(\texttt{a}\)等同,所以需要新开一个节点计算。
节点用结构体封装,复制\(q_{new}=q\)时把信息全部复制过去了,不要忘记把\(cnt\)改为\(0\)。
\(code\)
struct SuffixAutomaton {
struct node {
int ch[26],fa,len,cnt;
void clean() {
memset(ch,0,sizeof(ch));
fa = len = cnt = 0;
}
} S[maxn<<1];
int root,last,siz;
void init() {
for(int i = 1; i <= siz; i++)
S[i].clean();
root = last = siz = 1;
}
void insert(int c) {
int p = last, now = ++siz;
S[now].cnt = 1;
S[now].len = S[p].len+1;
for(; p && !S[p].ch[c]; p = S[p].fa)
S[p].ch[c] = now;
if(!p) S[now].fa = root;
else {
int q = S[p].ch[c];
if(S[q].len == S[p].len+1)
S[now].fa = q;
else {
int q_new = ++siz;
S[q_new] = S[q];
S[q_new].cnt = 0;
S[q_new].len = S[p].len+1;
S[now].fa = S[q].fa = q_new;
for(; p && S[p].ch[c] == q; p = S[p].fa)
S[p].ch[c] = q_new;
}
}
last = now;
}
} SAM;
模板题:Luogu P3804
求出\(S\)的所有出现次数\(>1\)的子串的(出现次数\(\times\)长度)\(_{max}\)。
由下到上更新\(parent\)树,最后计算每个节点的贡献即可。
为了保证由下到上更新,将节点按拓扑序排序。根据性质,一定有\(i.len<fa[i].len\)
因此,用桶排序将节点按\(len\)从大到小排序,得到的即为拓扑序。
将后缀链上的点的\(cnt\)设为\(1\),其余点设为\(0\)。
\(i.cnt = i.cnt + \sum j.cnt(fa[j]=i)\)
完整代码如下
#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#define MogeKo qwq
using namespace std;
const int maxn = 1e6+10;
char s[maxn];
int b[maxn<<1],que[maxn<<1];
long long ans;
struct SuffixAutomaton {
struct node {
int ch[26],fa,len,cnt;
void clean() {
memset(ch,0,sizeof(ch));
fa = len = cnt = 0;
}
} S[maxn<<1];
int root,last,siz;
void init() {
for(int i = 1; i <= siz; i++)
S[i].clean();
root = last = siz = 1;
}
void insert(int c) {
int p = last, now = ++siz;
S[now].cnt = 1;
S[now].len = S[p].len+1;
for(; p && !S[p].ch[c]; p = S[p].fa)
S[p].ch[c] = now;
if(!p) S[now].fa = root;
else {
int q = S[p].ch[c];
if(S[q].len == S[p].len+1)
S[now].fa = q;
else {
int q_new = ++siz;
S[q_new] = S[q];
S[q_new].cnt = 0;
S[q_new].len = S[p].len+1;
S[now].fa = S[q].fa = q_new;
for(; p && S[p].ch[c] == q; p = S[p].fa)
S[p].ch[c] = q_new;
}
}
last = now;
}
void calc() {
for(int i = 1; i <= siz; i++)
b[S[i].len]++;
for(int i = 1; i <= siz; i++)
b[i] += b[i-1];
for(int i = 1; i <= siz; i++)
que[b[S[i].len]--] = i;
for(int i = siz; i; i--)
S[S[que[i]].fa].cnt += S[que[i]].cnt;
for(int i = 1;i <= siz;i++)
if(S[i].cnt > 1) ans = max(ans,(long long)S[i].cnt*S[i].len);
printf("%lld",ans);
}
} SAM;
int main() {
scanf("%s",s+1);
int n = strlen(s+1);
SAM.init();
for(int i = 1; i <= n; i++)
SAM.insert(s[i]-‘a‘);
SAM.calc();
return 0;
}
标签:ret tps scanf -- 信息 初始 大小 代码 alc
原文地址:https://www.cnblogs.com/mogeko/p/13308090.html