标签：std   多边形   图片   return   奇数   最大   三角形   题解   acm   

J 数学/找规律

题意：

给定正n多边形，现在要你通过顶点连线的方式，将它划分完全划分成若干个三角形。我们定义两个三角形的距离为，两者相隔的完整的三角形数+1。

如下图，a与d的距离为3，a与c的距离为2

现在你要让所有两两三角形的距离中，最大距离的最小。求该最小值

（数据范围n为3-1e6）

题解

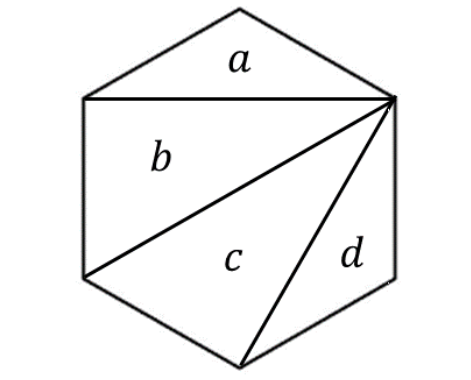
这个距离其实就是两个三角形之间隔离几条线(包括自身三角形的)

这题首先应该确定划分方案

由于分割出三角形的数量是一定的，说明线的数量也是一定的

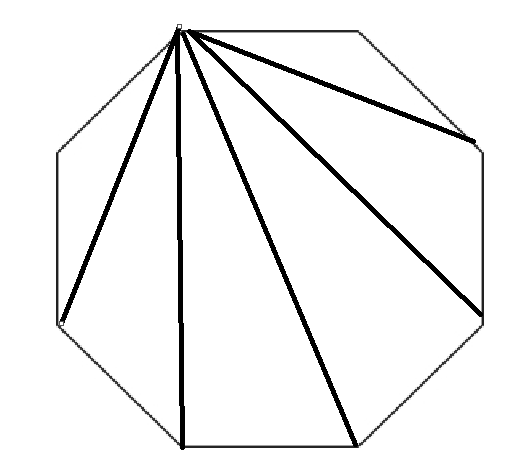
观察上图，不难发现，当某点集中了过多的线时，最大距离显然会很大，所以我们思路应该是让一定的线，尽量的分散他们的交点位置，如下图所示

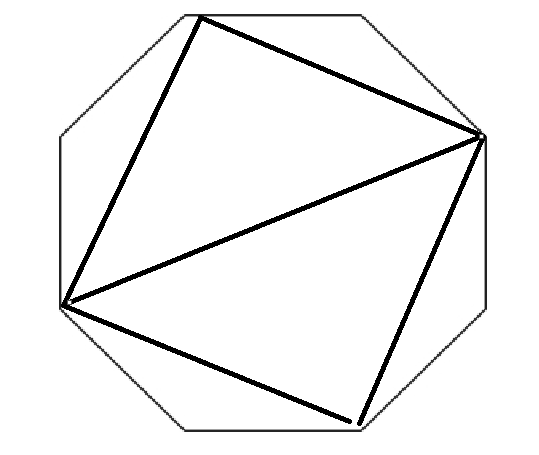
不难发现，下面的划分方案具有良好的推广性：

在未被划分的多边形内，以逆时针方向，依次选取三个点ABC，AC连线

接下来就是求最小值是多少了

依据我们上面这种划分规则，由于我们取的是最远距离，所以每多转一圈，我们肯定多一对线，即距离要+2

值得注意的是，如下图这种情况，奇数会少一条边，留给下圈逆时针

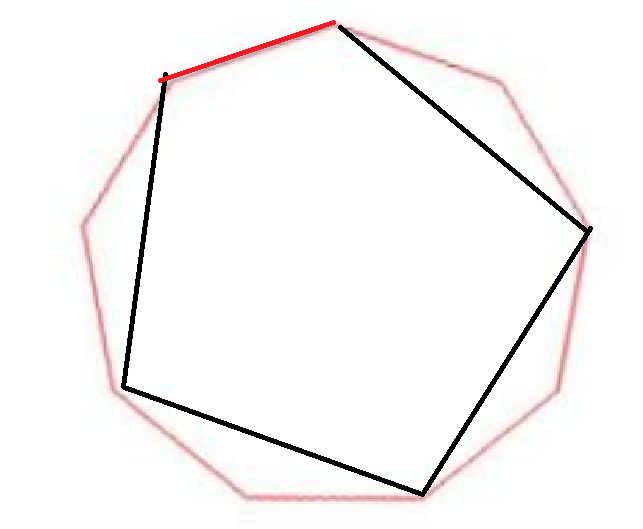
接下来只要递归计算一下就可以了，要留意递归终点。

标程

#include<iostream>
#include<cstring>
using namespace std;
int n;
int ans[11]={0,0,0,0,1,2,2,3,3,4,4};
int dfs(int x)
{
	if(x<=10)
	return ans[x];
	else
	{
		if(x%2)
		return dfs(x/2+1)+2;
		else
		return dfs(x/2)+2;
	}
}
int main()
{
	cin>>n;
	cout<<dfs(n);
	return 0;
}

2019ACM首尔J题题解

标签：std   多边形   图片   return   奇数   最大   三角形   题解   acm   

原文地址：https://www.cnblogs.com/et3-tsy/p/13324553.html