局部特征（Local Feature）

标签：tps   sdn   ide   拼接   span   asi   处理   学计算机   info   

文章首发：xmoon.info

对于图像处理时经常需要提取特征点分析图片结构，将照片进行拼接，实现全景拍摄，那么在照片特征点提取时所采用的具体算法是什么呢？

解决思路

1. 提取特征点
2. 匹配特征点
3. 使用RANSAC方法将两张图片的对应的特征点转换的方式拟合出来，在对图片采用相同的转换方式进行转换，在进行拼接

特征点——Corner

好的特征点是什么样的？

1. 可重复性：在一张图可以被观测到的，在其他同场景的图也可以被观测到
2. 显著性：检测的特征点需要是在某一类图像中“独有的”，尽量剔除“普遍性”的点，目的是为了将不同类的图区分开
3. 简洁和高效：尽可能的减少计算量，提高计算效率
4. 局部性：匹配特征时要匹配特征点之间的相对关系，通过局部特征相对位置来判断是否为同一张图，来拟合转动镜头角度，图像位置

什么样的点满足条件

通过观察图片的特征，发现存在“角”的地方承载着更多的信息，角点是梯度在两个或以上方向上有变化的点。

Basic Idea

1. 使用一个较小的窗口在图像上延各个方向滑动
2. 不同的变化趋势显示了不同的特征
3. 图像内部所在的窗口延各个方向都没有变化；边缘所在的窗口延边缘方向无变化；角点所在窗口会在各个方向上都有显著的变化
   

数学描述

• \(u\)和\(v\)是平移量
• 求平移后的窗口与平移前的窗口的对应位置差的平方，再累加
• 乘上窗口权重，考虑每个点对窗口影响的不同程度，例如第二种的高斯函数权重，就是考虑中间的点的差值在整个窗口的影响度更大
• 二阶泰勒展开：为了能够直接观察到\(E(u,v)\)与\([u,v]\)之间的联系

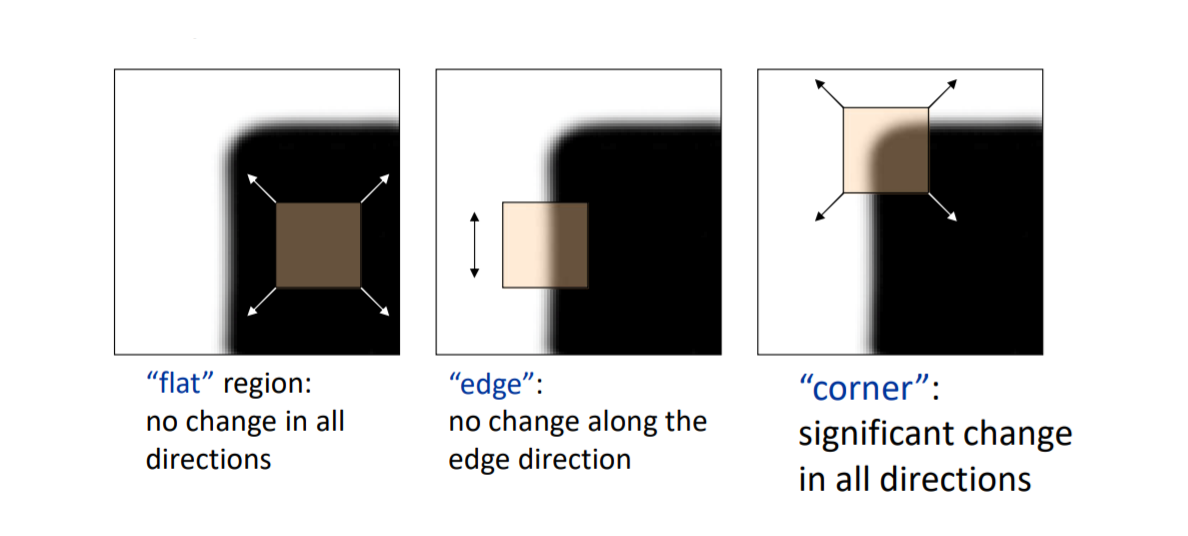
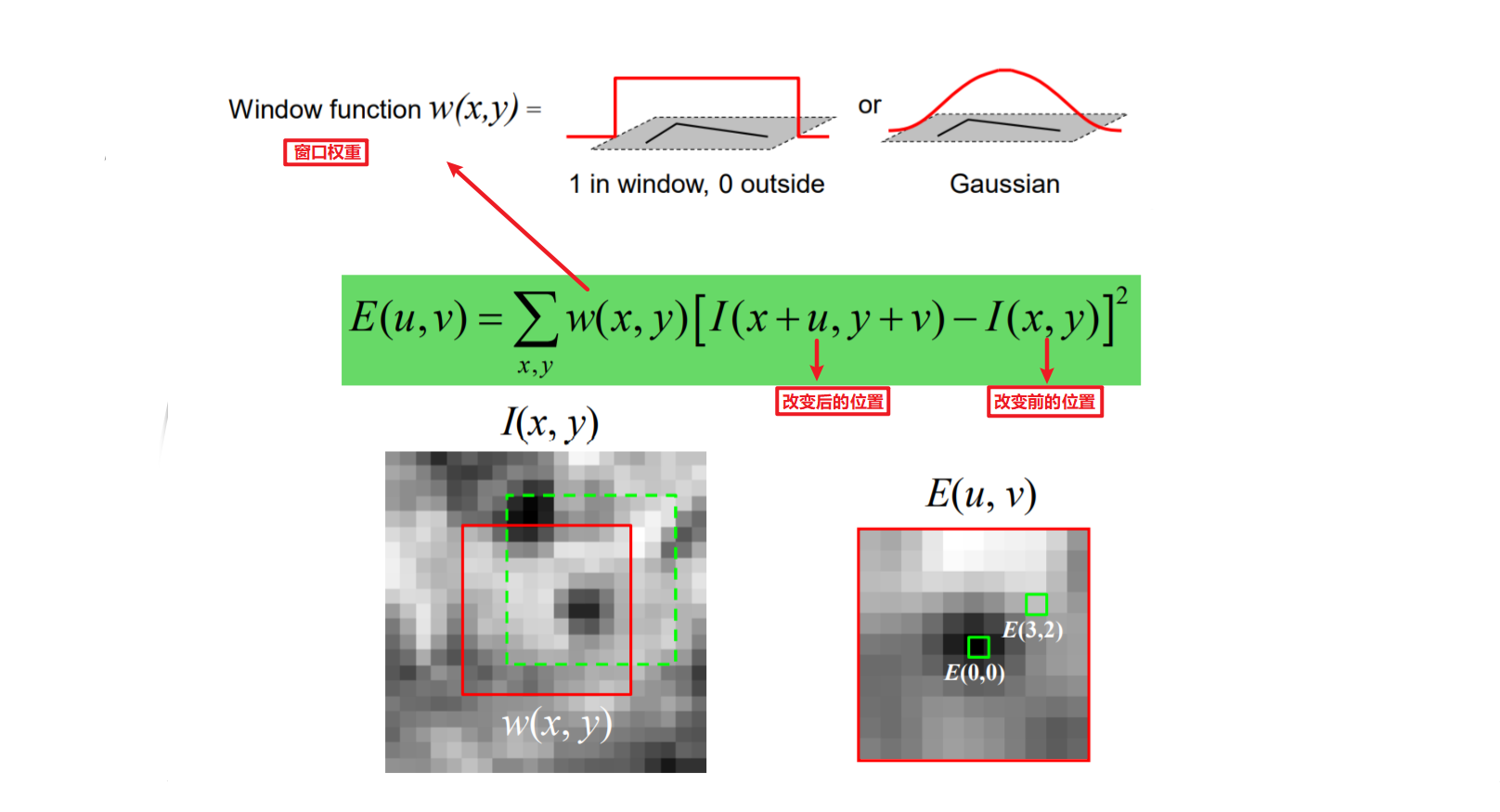
  取\(E(u,v)\)在\((0,0)\)的二阶展开作为近似解
  
  计算化简泰勒展开式
  
  其中\(I_x,I_y\)分别表示点\((x,y)\)在\(x\)方向,\(y\)方向的偏导，\(M\)是由一个二阶矩矩阵加权求和得到

矩阵\(M\)

类比方程\(y=ax+b\)决定方程特性的是\(a,b\)。则决定\(E(u,v)\)特性的是\(M\)，分析矩阵\(M\)就可以得到\(E(u,v)\)的特性

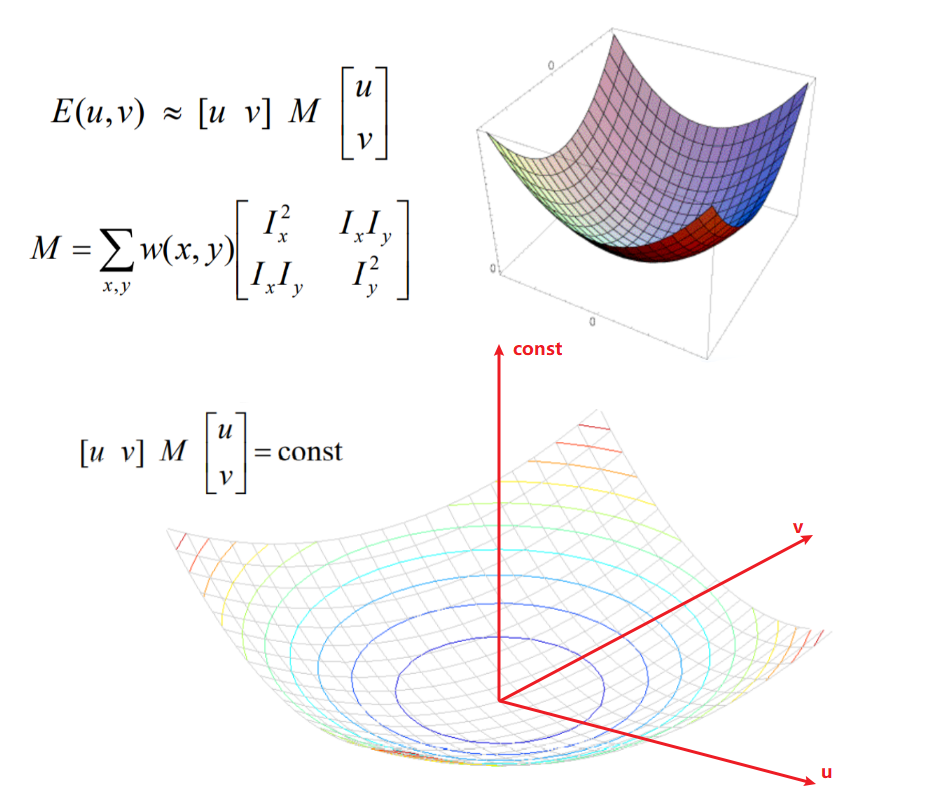
函数图像延竖直方向截取为一个椭圆，当梯度为零时，截面为圆，此时窗口位于图像内部；当延某一方向梯度为零时，界面为一个“正椭圆”，此时窗口位于边；当窗口位于角时，界面椭圆的形状反映了当前窗口下角的特性

• 正交矩阵\(R\)：使所截取的椭圆旋转\(R\)角度，变为一个“正椭圆”

  

  1. 当\(I_x,I_y\)任意一个趋于0，用\(\lambda\)表示，任意一个\(\lambda\)趋于0，都表示这个点不是角点
  2. 椭圆的半轴长度反应的是梯度变化的快慢，越长则梯度变化越快（将\(E(u,v)\)展开就可以得到椭圆的半轴表示为\(\lambda^{-\frac12}\)）

• 可视化
  

• 特征值简化——角点响应函数R
  
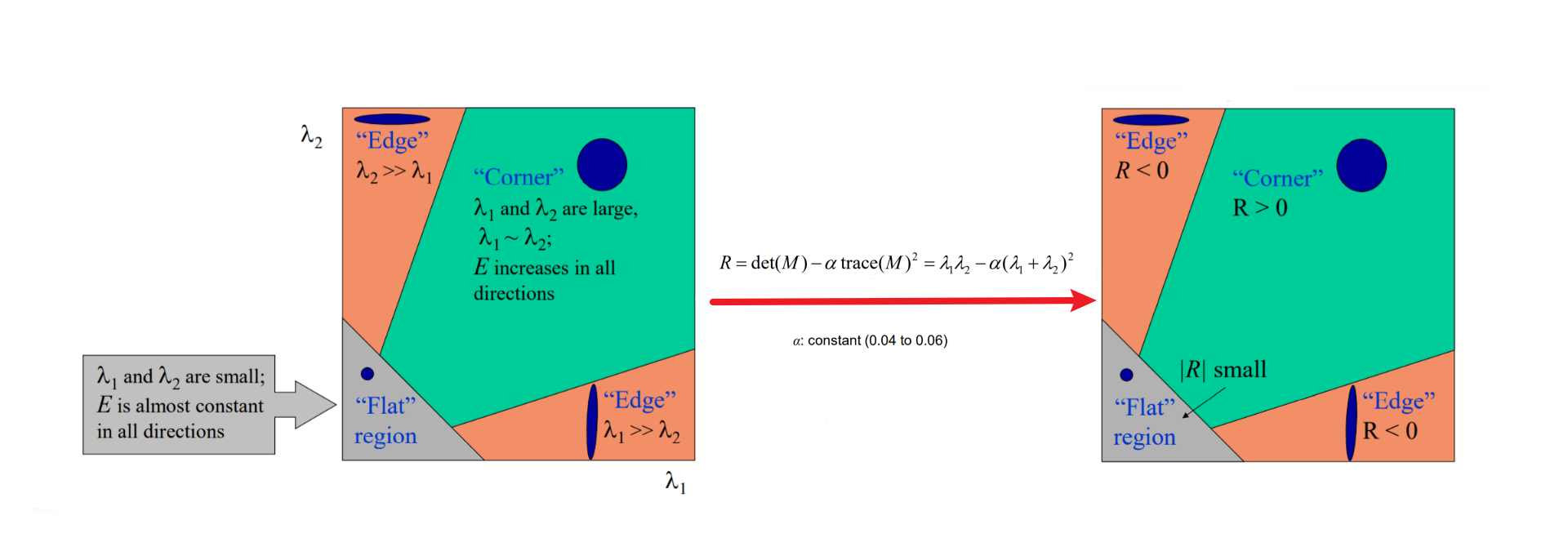
  将\(\lambda_1,\lambda_2\)特征转化给\(R\)，最后判断只需判断\(R\)就可以确定是否为角点

Harris检测器

1. 计算每个像素处的高斯导数
2. 计算每个像素周围的高斯窗口中的二阶矩矩阵M
3. 计算角点响应函数R
4. 设置门限R
5. 寻找响应函数的局部最大值(非最大抑制)

Harris的特性

1. 当光线强度，明暗改变时，只是改变了部分角点的值，还有大部分的点可以用于检测，可以进行检测，
2. 当改变位置，角度时，没有改变相对位置，可以检测
3. 当改变窗口大小时，大窗口下是角点，而小窗口下是线或者边缘，无法检测
   

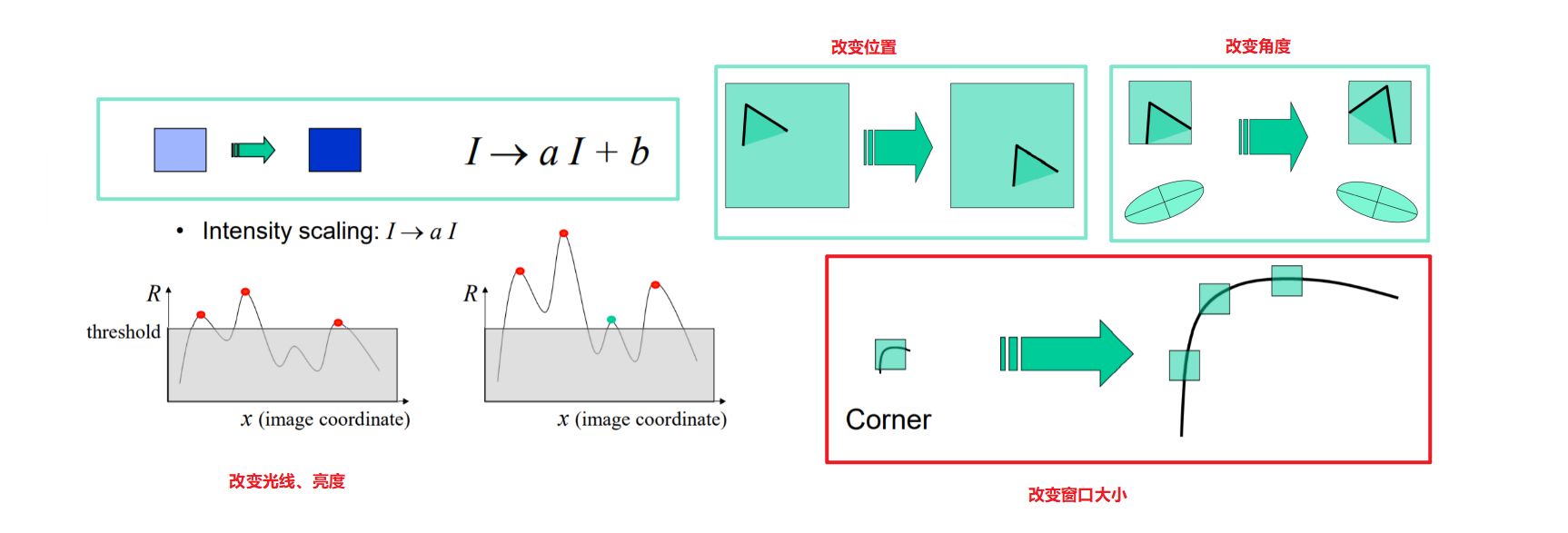
学习资源：北京邮电大学计算机视觉——鲁鹏

局部特征（Local Feature）

标签：tps   sdn   ide   拼接   span   asi   处理   学计算机   info   

原文地址：https://www.cnblogs.com/moonspace/p/13332735.html