标签:线性回归 log 假设 tip mic near repeat mamicode 矩阵转置
多维特征就是有多个特征,比如房价模型中增加房子的楼层数等等,模型的特征为\(\left( {x_{1}},{x_{2}},...,{x_{n}} \right)\)
\(n\) 代表特征的数量
\({x^{\left( i \right)}}\)代表第 \(i\) 个训练实例,是特征矩阵中的第\(i\)行,是一个向量(vector)。
例如:
\({x}^{(2)}\text{=}\begin{bmatrix} 1416\\\ 3\\\ 2\\\ 40 \end{bmatrix}\)
\({x}_{j}^{\left( i \right)}\)代表特征矩阵中第 \(i\) 行的第 \(j\) 个特征,也就是第 \(i\) 个训练实例的第 \(j\) 个特征。
如上图的\(x_{2}^{\left( 2 \right)}=3,x_{3}^{\left( 2 \right)}=2\),
支持多变量的假设 \(h\) 表示为:\(h_{\theta}\left( x \right)={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}}\),
为了使得公式能够简化一些,引入\(x_{0}=1\),则公式转化为:\(h_{\theta} \left( x \right)={\theta_{0}}{x_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}}\)
此时模型中的参数是一个\(n+1\)维的向量,任何一个训练实例也都是\(n+1\)维的向量,特征矩阵\(X\)的维度是 \(m*(n+1)\)。 因此公式可以简化为:\(h_{\theta} \left( x \right)={\theta^{T}}X\),其中上标\(T\)代表矩阵转置。
构建一个代价函数,这个代价函数是所有建模误差的平方和,即:\(J\left( {\theta_{0}},{\theta_{1}}...{\theta_{n}} \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( h_{\theta} \left({x}^{\left( i \right)} \right)-{y}^{\left( i \right)} \right)}^{2}}}\) ,
其中:\(h_{\theta}\left( x \right)=\theta^{T}X={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}}\)
梯度下降:
\({\theta_{j}}:={\theta_{j}}-\alpha \frac{\partial }{\partial {\theta_{j}}}J\left({\theta}_{0},{\theta}_{1},...,{\theta}_{n} \right)\)
在我们面对多维特征问题的时候,我们要保证这些特征都具有相近的尺度,这将帮助梯度下降算法更快地收敛。
最简单的方法是令:\({{x}_{n}}=\frac{{{x}_{n}}-{{\mu}_{n}}}{{{s}_{n}}}\),
其中 \({\mu_{n}}\)是平均值,\({s_{n}}\)是标准差。
梯度下降算法收敛所需要的迭代次数根据模型的不同而不同,我们不能提前预知,我们可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。
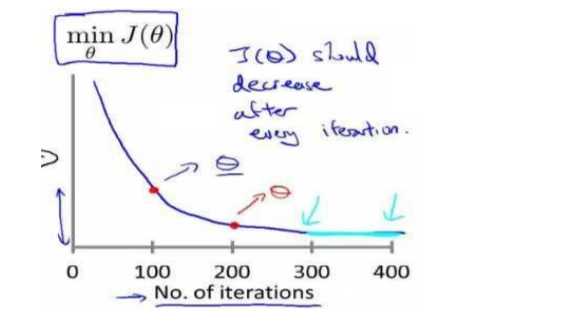
梯度下降算法的每次迭代受到学习率的影响,如果学习率\(a\)过小,则达到收敛所需的迭代次数会非常高;如果学习率\(a\)过大,每次迭代可能不会减小代价函数,可能会越过局部最小值导致无法收敛。
通常可以考虑尝试些学习率:
\(\alpha=0.01,0.03,0.1,0.3,1,3,10\)
线性回归并不适用于所有数据,有时我们需要曲线来适应我们的数据,比如一个二次方模型:\(h_{\theta}\left( x \right)={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}^2}\)
或者三次方模型: \(h_{\theta}\left( x \right)={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}^2}+{\theta_{3}}{x_{3}^3}\)
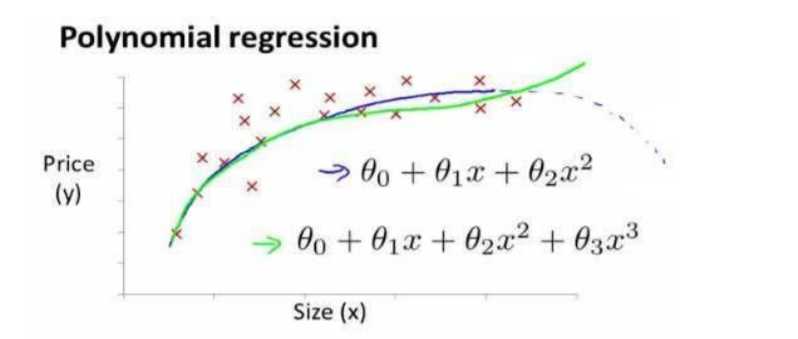
通常我们需要先观察数据然后再决定准备尝试怎样的模型。 另外,我们可以令:
\({{x}_{2}}=x_{2}^{2},{{x}_{3}}=x_{3}^{3}\),从而将模型转化为线性回归模型。
根据函数图形特性,我们还可以使:
\({{{h}}_{\theta}}(x)={{\theta }_{0}}\text{+}{{\theta }_{1}}(size)+{{\theta}_{2}}{{(size)}^{2}}\)
或者:
\({{{h}}_{\theta}}(x)={{\theta }_{0}}\text{+}{{\theta }_{1}}(size)+{{\theta }_{2}}\sqrt{size}\)
注:如果我们采用多项式回归模型,在运行梯度下降算法前,特征缩放非常有必要。
除了梯度下降法外,对于某些线性回归问题我们可以直接通过正规方程求出\({\theta}\).
即求解方程:\(\frac{\partial}{\partial{\theta_{j}}}J\left( {\theta_{j}} \right)=0\) 。
假设我们的训练集特征矩阵为 \(X\)(包含了 \({{x}_{0}}=1\))并且我们的训练集结果为向量 \(y\),则利用正规方程解出向量 \(\theta ={{\left( {X^T}X \right)}^{-1}}{X^{T}}y\) 。
梯度下降与正规方程的比较:
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择学习率\(\alpha\) | 不需要 |
| 需要多次迭代 | 一次运算得出 |
| 当特征数量\(n\)大时也能较好适用 | 需要计算\({{\left( {{X}^{T}}X \right)}^{-1}}\) 如果特征数量n较大则运算代价大,因为矩阵逆的计算时间复杂度为\(O\left( {{n}^{3}} \right)\),通常来说当\(n\)小于10000 时还是可以接受的 |
| 适用于各种类型的模型 | 只适用于线性模型,不适合逻辑回归模型等其他模型 |
特征变量小于1w通常用正规方程,大于1w更倾向于使用梯度下降
正规方程的python实现:
import numpy as np
def normalEqn(X, y):
theta = np.linalg.inv(X.T@X)@X.T@y #X.T@X等价于X.T.dot(X)
return theta
对于二元分类问题
我们将因变量(dependent variable)可能属于的两个类分别称为负向类(negative class)和正向类(positive class),则因变量\(y\in { 0,1 \\}\) ,其中 0 表示负向类,1 表示正向类。
由于y是离散的(0或1),如果使用线性回归的话输出的y可能远大于1或远小于0,这与我们的条件不符,而逻辑回归的特征就是它的输出值永远在0和1之间。
逻辑回归是一种分类算法,适用于标签y取值离散的情况
我们引入一个新的模型,逻辑回归,该模型的输出变量范围始终在0和1之间。
逻辑回归模型的假设是: \(h_\theta \left( x \right)=g\left(\theta^{T}X \right)\)
其中:
\(X\) 代表特征向量
\(g\) 代表逻辑函数(logistic function)是一个常用的逻辑函数为S形函数(Sigmoid function),公式为: \(g\left( z \right)=\frac{1}{1+{{e}^{-z}}}\)。
python代码实现:
import numpy as np
def sigmoid(z):
return 1 / (1 + np.exp(-z))
该函数的图像为:
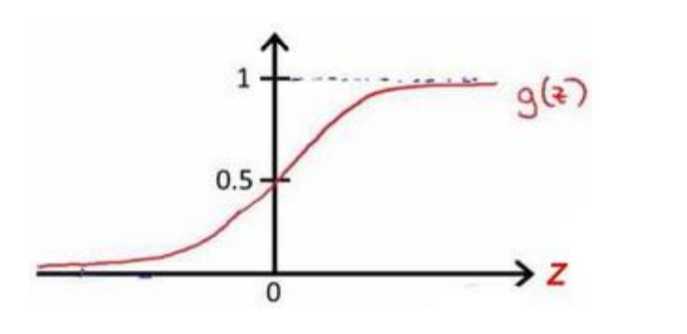
合起来,我们得到逻辑回归模型的假设:
对模型的理解: \(g\left( z \right)=\frac{1}{1+{{e}^{-z}}}\)。
\(h_\theta \left( x \right)\)的作用是,对于给定的输入变量,根据选择的参数计算输出变量=1的可能性(estimated probablity)
即
\(h_\theta \left( x \right)=P\left( y=1|x;\theta \right)\) (就是一个条件概率)
例如,如果对于给定的\(x\),通过已经确定的参数计算得出\(h_\theta \left( x \right)=0.7\),则表示有70%的几率\(y\)为正向类,相应地\(y\)为负向类的几率为1-0.7=0.3。
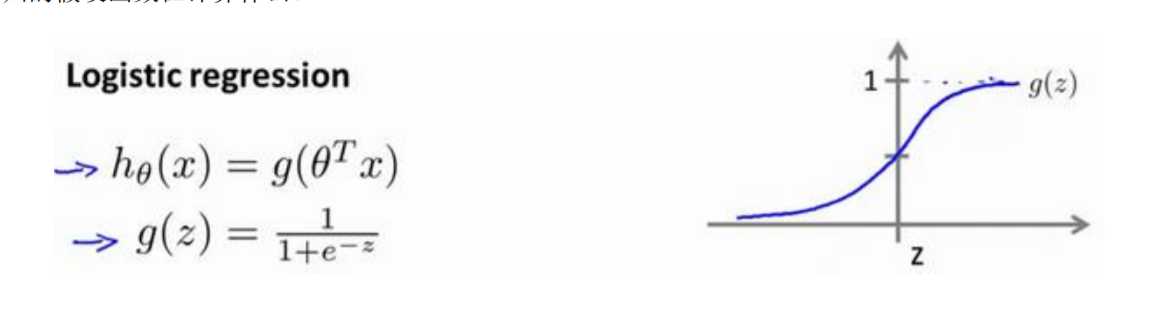
在逻辑回归中,我们预测:
当\({h_\theta}\left( x \right)>=0.5\)时,预测 \(y=1\)。
当\({h_\theta}\left( x \right)<0.5\)时,预测 \(y=0\) 。
根据上面绘制出的 S 形函数图像,我们知道当
\(z=0\) 时 \(g(z)=0.5\)
\(z>0\) 时 \(g(z)>0.5\)
\(z<0\) 时 \(g(z)<0.5\)
又 \(z={\theta^{T}}x\) ,即:
\({\theta^{T}}x>=0\) 时,预测 \(y=1\)
\({\theta^{T}}x<0\) 时,预测 \(y=0\)
现在假设我们有一个模型:
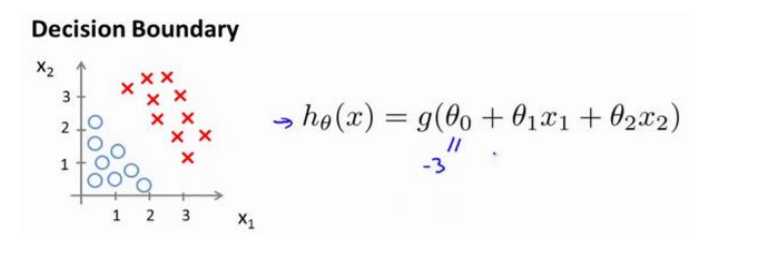
并且参数\(\theta\) 是向量[-3 1 1]。 则当\(-3+{x_1}+{x_2} \geq 0\),即\({x_1}+{x_2} \geq 3\)时,模型将预测 \(y=1\)。
我们可以绘制直线\({x_1}+{x_2} = 3\),这条线便是我们模型的分界线,将预测为1的区域和预测为 0的区域分隔开。
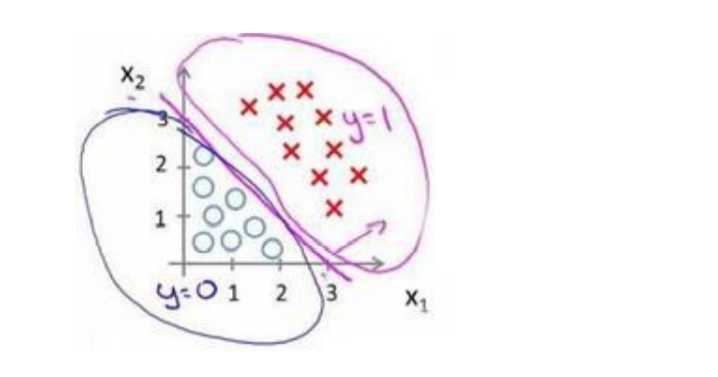
假使我们的数据呈现这样的分布情况,怎样的模型才能适合呢?
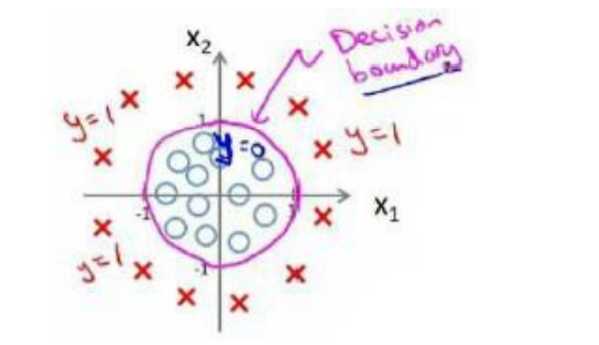
因为需要用曲线才能分隔 \(y=0\) 的区域和 \(y=1\) 的区域,我们需要二次方特征:\({h_\theta}\left( x \right)=g\left( {\theta_0}+{\theta_1}{x_1}+{\theta_{2}}{x_{2}}+{\theta_{3}}x_{1}^{2}+{\theta_{4}}x_{2}^{2} \right)\)是[-1 0 0 1 1],则我们得到的判定边界恰好是圆点在原点且半径为1的圆形。
我们可以用非常复杂的模型来适应非常复杂形状的判定边界。
我们用代价函数来拟合参数\({\theta}\)
对于线性回归模型,我们定义的代价函数是所有模型误差的平方和。理论上来说,我们也可以对逻辑回归模型沿用这个定义,但是问题在于,当我们将\({h_\theta}\left( x \right)=\frac{1}{1+{e^{-\theta^{T}x}}}\)带入到这样定义了的代价函数中时,我们得到的代价函数将是一个非凸函数(non-convexfunction)
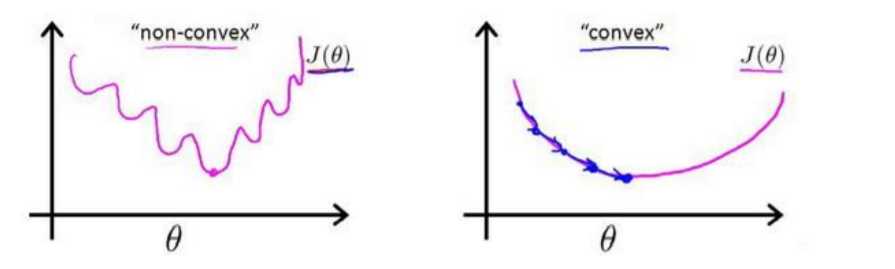
这意味着我们的代价函数有许多局部最小值,这将影响梯度下降算法寻找全局最小值。
线性回归的代价函数为:\(J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{\frac{1}{2}{{\left( {h_\theta}\left({x}^{\left( i \right)} \right)-{y}^{\left( i \right)} \right)}^{2}}}\) 。
我们重新定义逻辑回归的代价函数为:\(J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{{Cost}\left( {h_\theta}\left( {x}^{\left( i \right)} \right),{y}^{\left( i \right)} \right)}\),其中
\({h_\theta}\left( x \right)\)与 \(Cost\left( {h_\theta}\left( x \right),y \right)\)之间的关系如下图所示:
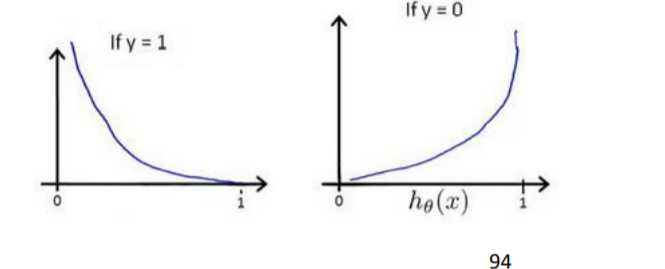
这样构建的\(Cost\left( {h_\theta}\left( x \right),y \right)\)函数的特点是:当实际的 \(y=1\) 且\({h_\theta}\left( x \right)\)也为 1 时误差为 0,当 \(y=1\) 但\({h_\theta}\left( x \right)\)不为1时误差随着\({h_\theta}\left( x \right)\)变小而变大;当实际的 \(y=0\) 且\({h_\theta}\left( x \right)\)也为 0 时代价为 0,当\(y=0\) 但\({h_\theta}\left( x \right)\)不为 0时误差随着 \({h_\theta}\left( x \right)\)的变大而变大。
将构建的 \(Cost\left( {h_\theta}\left( x \right),y \right)\)简化如下:
\(Cost\left( {h_\theta}\left( x \right),y \right)=-y\times log\left( {h_\theta}\left( x \right) \right)-(1-y)\times log\left( 1-{h_\theta}\left( x \right) \right)\)
带入代价函数得到:
\(J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{[-{{y}^{(i)}}\log \left( {h_\theta}\left( {{x}^{(i)}} \right) \right)-\left( 1-{{y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( {{x}^{(i)}} \right) \right)]}\)
即:\(J\left( \theta \right)=-\frac{1}{m}\sum\limits_{i=1}^{m}{[{{y}^{(i)}}\log \left( {h_\theta}\left( {{x}^{(i)}} \right) \right)+\left( 1-{{y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( {{x}^{(i)}} \right) \right)]}\)
Python代码实现:
import numpy as np
def cost(theta, X, y):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
first = np.multiply(-y, np.log(sigmoid(X* theta.T)))
second = np.multiply((1 - y), np.log(1 - sigmoid(X* theta.T)))
return np.sum(first - second) / (len(X))
在得到这样一个代价函数以后,我们便可以用梯度下降算法来求得能使代价函数最小的参数了。算法为:
Repeat {
\(\theta_j := \theta_j - \alpha \frac{\partial}{\partial\theta_j} J(\theta)\)
(simultaneously update all )
}
求导后得到:
Repeat {
\(\theta_j := \theta_j - \alpha \frac{1}{m}\sum\limits_{i=1}^{m}{{\left( {h_\theta}\left( \mathop{x}^{\left( i \right)} \right)-\mathop{y}^{\left( i \right)} \right)}}\mathop{x}_{j}^{(i)}\)
(simultaneously update all )
}
一些梯度下降算法之外的选择:
除了梯度下降算法以外,还有一些常被用来令代价函数最小的算法,这些算法更加复杂和优越,而且通常不需要人工选择学习率,通常比梯度下降算法要更加快速。这些算法有:共轭梯度(Conjugate Gradient),局部优化法(Broyden fletcher goldfarb shann,BFGS)和有限内存局部优化法(LBFGS)
逻辑回归的代价函数:
\(Cost\left( {h_\theta}\left( x \right),y \right)=-y\times log\left( {h_\theta}\left( x \right) \right)-(1-y)\times log\left( 1-{h_\theta}\left( x \right) \right)\)
\(=-\frac{1}{m}\sum\limits_{i=1}^{m}{[{{y}^{(i)}}\log \left( {h_\theta}\left( {{x}^{(i)}} \right) \right)+\left( 1-{{y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( {{x}^{(i)}} \right) \right)]}\)
使用梯度下降法最小化代价函数
\(J\left( \theta \right)=-\frac{1}{m}\sum\limits_{i=1}^{m}{[{{y}^{(i)}}\log \left( {h_\theta}\left( {{x}^{(i)}} \right) \right)+\left( 1-{{y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( {{x}^{(i)}} \right) \right)]}\)
用这个式子更新所有theta值
\({\theta_j}:={\theta_j}-\alpha \frac{1}{m}\sum\limits_{i=1}^{m}{({h_\theta}({{x}^{(i)}})-{{y}^{(i)}}){x_{j}}^{(i)}}\)
把这个偏导数项\(\frac{\partial }{\partial {\theta_j}}J\left( \theta \right)\)放回到原来式子这里,我们就可以将梯度下降算法写作如下形式:
\({\theta_j}:={\theta_j}-\alpha \frac{1}{m}\sum\limits_{i=1}^{m}{({h_\theta}({{x}^{(i)}})-{{y}^{(i)}}){x_{j}}^{(i)}}\)
虽然式子看似相同,但线性回归梯度下降和逻辑回归梯度下降是不同的
对于线性回归假设函数:
\({h_\theta}\left( x \right)={\theta^T}X={\theta_{0}}{x_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}}\)
而现在逻辑函数假设函数:
\({h_\theta}\left( x \right)=\frac{1}{1+{{e}^{-{\theta^T}X}}}\)
因此,即使更新参数的规则看起来基本相同,但由于假设的定义发生了变化,所以逻辑函数的梯度下降,跟线性回归的梯度下降实际上是两个完全不同的东西。
特征缩放的方法,也适用于逻辑回归。如果你的特征范围差距很大的话,那么应用特征缩放的方法,同样也可以让逻辑回归中,梯度下降收敛更快
一对多的数据集和二元数据集
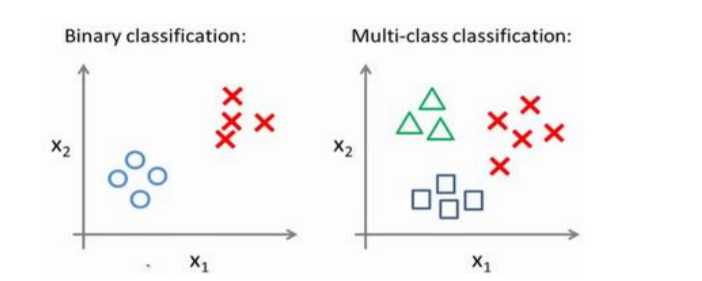
对于一对多的分类工作,我们使用一对余的方法,即将其分为多个二元分类问题
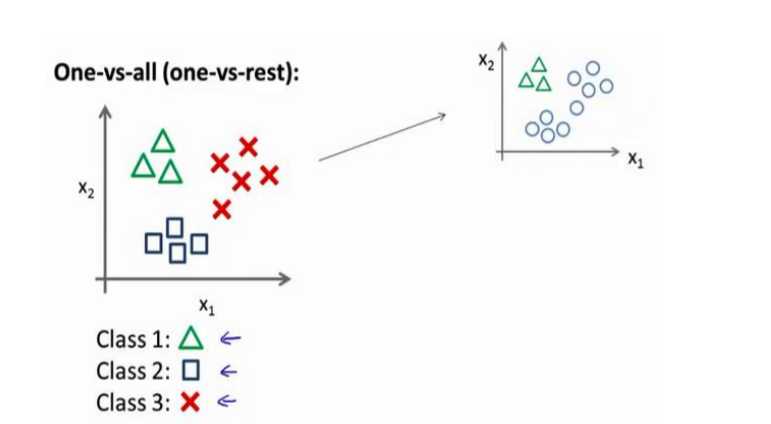
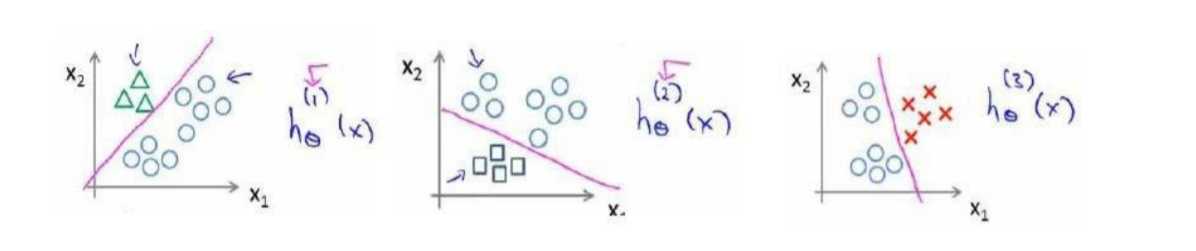
我们将多个类中的一个类标记为正向类(\(y=1\)),然后将其他所有类都标记为负向类,这个模型记作\(h_\theta^{\left( 1 \right)}\left( x \right)\)。接着,类似地第我们选择另一个类标记为正向类(\(y=2\)),再将其它类都标记为负向类,将这个模型记作 \(h_\theta^{\left( 2 \right)}\left( x \right)\),依此类推。
最后我们得到一系列的模型简记为: \(h_\theta^{\left( i \right)}\left( x \right)=p\left( y=i|x;\theta \right)\)其中:\(i=\left( 1,2,3....k \right)\)
最后,在我们需要做预测时,我们将所有的分类机都运行一遍,然后对每一个输入变量,都选择最高可能性的输出变量。
标签:线性回归 log 假设 tip mic near repeat mamicode 矩阵转置
原文地址:https://www.cnblogs.com/muyefeiwu/p/13332641.html